Functions of a complex variable, theory of
In the broad sense of the term, the theory of functions defined on some set of points  in the complex plane
in the complex plane 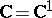 (functions of a single complex variable) or on a set of points
(functions of a single complex variable) or on a set of points 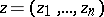 of a complex Euclidean space
of a complex Euclidean space  ,
, 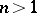 (functions of several complex variables). In the narrow sense of the term, the theory of function of a complex variable is the theory of analytic functions (cf. Analytic function) of one or several complex variables.
(functions of several complex variables). In the narrow sense of the term, the theory of function of a complex variable is the theory of analytic functions (cf. Analytic function) of one or several complex variables.
As an independent discipline, the theory of functions of a complex variable took shape in about the middle of the 19th century as the theory of analytic functions. The fundamental work here was that of A.L. Cauchy, K. Weierstrass and B. Riemann, who approached the development of the theory from various (different) points of view.
According to Weierstrass, a function 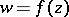 is called analytic (or holomorphic) in a domain
is called analytic (or holomorphic) in a domain 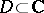 if it can be expanded in a power series in a neighbourhood of each point
if it can be expanded in a power series in a neighbourhood of each point 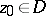 :
:
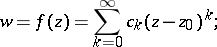 | (1) |
in the case of several complex variables, when 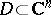 ,
, 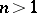 , the series (1) is interpreted as a multiple power series. To define an analytic function it is even sufficient that the convergent series (1) be given in a neighbourhood of a single point
, the series (1) is interpreted as a multiple power series. To define an analytic function it is even sufficient that the convergent series (1) be given in a neighbourhood of a single point 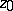 , for its values at another point
, for its values at another point 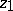 and the corresponding series can be determined by the process of analytic continuation along various paths in the complex plane
and the corresponding series can be determined by the process of analytic continuation along various paths in the complex plane 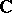 (or in
(or in 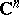 ,
, 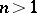 ) joining
) joining 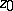 and
and 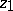 .
.
In the course of analytic continuation one may come across singular points (cf. Singular point), to which it is impossible to carry out analytic continuation along any path. These singular points determine the general behaviour of an analytic function in the sense that if two paths 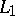 and
and 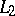 joining the same fixed points
joining the same fixed points 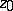 and
and 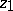 are not homotopic, that is, if it is impossible to deform
are not homotopic, that is, if it is impossible to deform 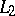 continuously into
continuously into 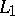 without thereby passing through any singular point, then the values of the function
without thereby passing through any singular point, then the values of the function  obtained by analytic continuation along
obtained by analytic continuation along 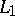 and
and 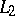 may turn out to be different. Consequently, the complete analytic function
may turn out to be different. Consequently, the complete analytic function 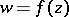 obtained by analytic continuation of an initial element (1) along all possible paths may turn out to be multiple-valued in its natural domain of definition in
obtained by analytic continuation of an initial element (1) along all possible paths may turn out to be multiple-valued in its natural domain of definition in 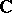 (or in
(or in 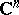 ,
, 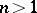 ). Examples of this are the functions
). Examples of this are the functions  or
or 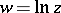 . One can escape from this multiple-valuedness by forbidding analytic continuation along certain paths, by constructing so-called cuts in the complex plane, and by distinguishing single-valued branches of an analytic function (cf. Branch of an analytic function). But the most perfect method of converting a multiple-valued function into a single-valued one consists in regarding it not as a function of a point of the complex plane, but as a function of a point of a Riemann surface, consisting of several sheets that cover the complex plane, and joined to one another in a certain way. In the case of several variables, instead of a Riemann surface there arises a Riemannian domain, a multiple-sheeted cover of
. One can escape from this multiple-valuedness by forbidding analytic continuation along certain paths, by constructing so-called cuts in the complex plane, and by distinguishing single-valued branches of an analytic function (cf. Branch of an analytic function). But the most perfect method of converting a multiple-valued function into a single-valued one consists in regarding it not as a function of a point of the complex plane, but as a function of a point of a Riemann surface, consisting of several sheets that cover the complex plane, and joined to one another in a certain way. In the case of several variables, instead of a Riemann surface there arises a Riemannian domain, a multiple-sheeted cover of 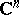 ,
, 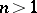 .
.
In his construction of the theory of analytic functions, Cauchy started from the concept of monogeneity. He called a function 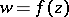 ,
, 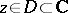 , monogenic if it has a monodromic (that is, single-valued and continuous, except for poles) derivative everywhere in
, monogenic if it has a monodromic (that is, single-valued and continuous, except for poles) derivative everywhere in 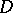 . Extending this concept somewhat, by a monogenic function
. Extending this concept somewhat, by a monogenic function 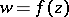 on a subset
on a subset 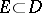 one usually means a (single-valued) function for which there exists at all points
one usually means a (single-valued) function for which there exists at all points  a derivative with respect to
a derivative with respect to 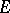 ,
,
 | (2) |
Monogeneity in the sense of Cauchy is the same as analyticity when  . Cauchy developed the theory of integration of analytic functions, proved the important theorem on residues (cf. Residue of an analytic function), the Cauchy integral theorem, and introduced the concept of the Cauchy integral:
. Cauchy developed the theory of integration of analytic functions, proved the important theorem on residues (cf. Residue of an analytic function), the Cauchy integral theorem, and introduced the concept of the Cauchy integral:
 | (3) |
which expresses the value of an analytic function  in terms of its values on any closed contour
in terms of its values on any closed contour  surrounding
surrounding  and not containing any singular points of
and not containing any singular points of 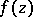 inside or on
inside or on 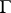 . As the simplest integral representation of analytic functions, the concept of the Cauchy integral can also be retained for functions of several variables.
. As the simplest integral representation of analytic functions, the concept of the Cauchy integral can also be retained for functions of several variables.
If one introduces complex variables 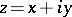 ,
, 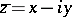 , one can describe any function of two variables
, one can describe any function of two variables  and
and 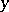 ,
, 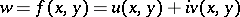 , as a function of
, as a function of  and
and  . The Cauchy–Riemann conditions, which pick out those among such functions that are analytic, demand that the functions
. The Cauchy–Riemann conditions, which pick out those among such functions that are analytic, demand that the functions 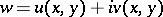 be differentiable with respect to both variables
be differentiable with respect to both variables 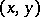 , while everywhere in
, while everywhere in 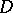 the equation
the equation
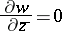 | (4) |
must hold, or, in full,  ,
,  .
.
The conditions (4) mean that the real and imaginary parts 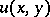 and
and 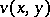 of an analytic function must be conjugate harmonic functions. In the case of analytic functions of several complex variables, the conditions (4) must be satisfied with respect to all the variables
of an analytic function must be conjugate harmonic functions. In the case of analytic functions of several complex variables, the conditions (4) must be satisfied with respect to all the variables 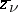 ,
, 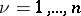 .
.
For Riemann, the most important thing was the circumstance that an analytic function 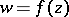 , as picked out by the conditions (4), effects, under certain conditions, a conformal mapping of
, as picked out by the conditions (4), effects, under certain conditions, a conformal mapping of 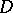 onto some other domain in the plane of the complex variable
onto some other domain in the plane of the complex variable 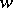 . The connection between analytic functions and conformal mappings opens a way to solving a number of problems in mathematical physics.
. The connection between analytic functions and conformal mappings opens a way to solving a number of problems in mathematical physics.
The subsequent development of the theory of functions of a complex variable has been and still is above all a deepening and extension of the theory of analytic functions (see, for example, Boundary value problems of analytic function theory; Boundary properties of analytic functions; Uniqueness properties of analytic functions; Integral representation of an analytic function; Meromorphic function; Multivalent function; Univalent function; Entire function). Problems, related to analytic functions, of approximation and interpolation of functions have an important significance. In these it turns out that in the theory of analytic functions of several variables the specific nature and difficulty of the problems are such that they only yield a solution when one invokes the most modern methods of algebra, topology and analysis.
The boundary properties of holomorphic functions, in particular of the integral of Cauchy type (see Cauchy integral) obtained from (3) when the values of 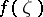 on the contour
on the contour 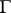 are given totally arbitrarily, are of great theoretical and practical significance, as are multi-dimensional analogues of this and other integral representations.
are given totally arbitrarily, are of great theoretical and practical significance, as are multi-dimensional analogues of this and other integral representations.
Generalized analytic functions (cf. Generalized analytic function), which are important for applications, are obtained in their simplest form as solutions of an equation generalizing (4):
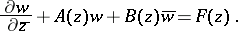 |
Their main properties (in the case of a single variable) have been investigated in fair detail.
The study of quasi-conformal mappings (cf. Quasi-conformal mapping) is of great significance for the theory of analytic functions itself (in particular, for the theory of Riemann surfaces) and for its applications.
A theory of abstract analytic functions (cf. Abstract analytic function) with values in various vector spaces has also been developed.
References
| [1] | I.I. [I.I. Privalov] Priwalow, "Einführung in die Funktionentheorie" , 1–3 , Teubner (1958–1959) (Translated from Russian) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian) |
| [3] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [4] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [5] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1969) (In Russian) |
| [6] | I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian) |
| [7] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) |
| [8] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [9] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) |
Comments
References
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. 24–26 |
| [a2] | C. Carathéodory, "Theory of functions of a complex variable" , 1–2 , Chelsea, reprint (1964) (Translated from German) |
| [a3] | J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) pp. 40 |
| [a4] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1987) pp. 24 |
| [a5] | S. Saks, A. Zygmund, "Analytic functions" , PWN (1965) (Translated from Polish) |
| [a6] | J.B. Conway, "Functions of a complex variable" , Springer (1973) |
| [a7] | E. Hille, "Analytic function theory" , 1–2 , Chelsea, reprint (1974) |
| [a8] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) |
| [a9] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. 6 |
| [a10] | R.P. Boas, "Invitation to complex analysis" , Random House (1987) |
| [a11] | R.B. Burckell, "An introduction to classical complex analysis" , 1 , Acad. Press (1979) |
| [a12] | P. Henrici, "Applied and computational complex analysis" , 1–3 , Wiley (1974–1986) |
| [a13] | M. Heins, "Complex function theory" , Acad. Press (1968) |
| [a14] | R. Narasimhan, "Complex analysis in one variable" , Birkhäuser (1985) |
Functions of a complex variable, theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functions_of_a_complex_variable,_theory_of&oldid=17625