Fuchsian equation
equation of Fuchsian class
A linear homogeneous ordinary differential equation in the complex domain,
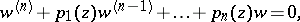 | (1) |
with analytic coefficients, all singular points of which on the Riemann sphere are regular singular points (cf. Regular singular point). Equation (1) belongs to the Fuchsian class if and only if its coefficients have the form
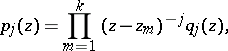 |
where  are distinct points and
are distinct points and 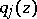 is a polynomial of degree
is a polynomial of degree 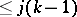 . A system
. A system 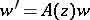 of
of  equations belongs to the Fuchsian class if it has the form
equations belongs to the Fuchsian class if it has the form
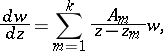 | (2) |
where  are distinct points and the
are distinct points and the 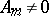 are constant
are constant 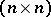 -dimensional matrices. The points
-dimensional matrices. The points 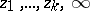 are singular for the equation (1) and the system (2). Fuchs' identity holds for (1):
are singular for the equation (1) and the system (2). Fuchs' identity holds for (1):
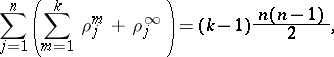 |
where 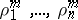 are the characteristic exponents at
are the characteristic exponents at 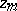 , and
, and 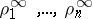 those at
those at 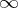 (cf. Characteristic exponent). Fuchsian equations (and systems) are also called regular equations (systems). This class of equations and systems was introduced by J.L. Fuchs .
(cf. Characteristic exponent). Fuchsian equations (and systems) are also called regular equations (systems). This class of equations and systems was introduced by J.L. Fuchs .
Let 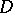 be the Riemann sphere with punctures at the points
be the Riemann sphere with punctures at the points 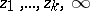 . Every non-trivial solution of (1) (respectively, every component of a solution of (2)) is an analytic function in
. Every non-trivial solution of (1) (respectively, every component of a solution of (2)) is an analytic function in  . In general, this function is infinite-valued, and all the singular points of (1) (or (2)) are branch points of it of infinite order.
. In general, this function is infinite-valued, and all the singular points of (1) (or (2)) are branch points of it of infinite order.
A second-order Fuchsian equation with singular points  has the form
has the form
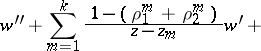 | (3) |
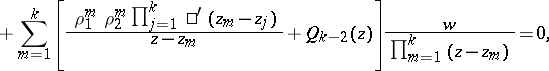 |
where 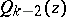 is a polynomial of degree
is a polynomial of degree 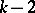 . The transformation
. The transformation 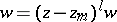 takes a Fuchsian equation to a Fuchsian equation, with
takes a Fuchsian equation to a Fuchsian equation, with
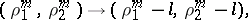 |
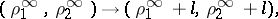 |
and the characteristic exponents at the other singular points are unchanged. By means of such transformations, equation (3) can be reduced to the form
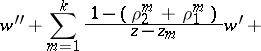 |
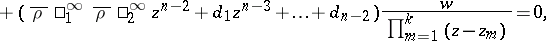 |
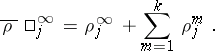 |
A second-order Fuchsian equation with  singular points is completely determined by specifying the values of the characteristic exponents at these points if and only if
singular points is completely determined by specifying the values of the characteristic exponents at these points if and only if 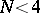 . Using a Möbius transformation the equation can be reduced to the form: a)
. Using a Möbius transformation the equation can be reduced to the form: a) 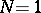 ,
, 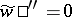 ; b)
; b) 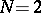 ,
, 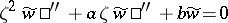 (the Euler equation); c)
(the Euler equation); c) 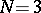 — the Papperitz equation (or Riemann equation).
— the Papperitz equation (or Riemann equation).
A matrix Fuchsian equation has the form
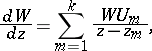 | (4) |
where  are distinct points,
are distinct points, 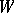 is an
is an 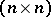 -dimensional matrix function, and the
-dimensional matrix function, and the 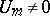 are constant matrices. The matrix
are constant matrices. The matrix 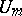 is called a differential substitution at
is called a differential substitution at 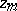 . Let
. Let 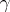 be a closed curve that starts at a non-singular point
be a closed curve that starts at a non-singular point 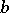 , is positively oriented and contains only the singular point
, is positively oriented and contains only the singular point 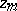 inside it. If
inside it. If  is a solution of (4) that is holomorphic at
is a solution of (4) that is holomorphic at 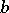 , then under analytic continuation along
, then under analytic continuation along 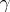 ,
,
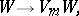 | (5) |
where 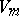 is a constant matrix, called an integral substitution at
is a constant matrix, called an integral substitution at 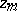 . H. Poincaré (see [2]) posed the so-called first regular Poincaré problem for a system of the form (4). It consists of the following three problems:
. H. Poincaré (see [2]) posed the so-called first regular Poincaré problem for a system of the form (4). It consists of the following three problems:
A) to represent the solution 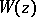 in its whole domain of existence;
in its whole domain of existence;
B) to construct the integral substitutions at the points 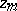 ;
;
C) to give an analytic characterization of the singularities of the solutions.
In particular, solving problem B) enables one to construct the monodromy group of (4). A solution of the Poincaré problem was obtained by I.A. Lappo-Danilevskii [3]. Let 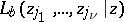 ,
, 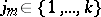 ,
, 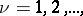 be the hyperlogarithms:
be the hyperlogarithms:
 |
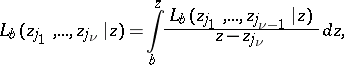 |
let 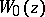 be the element (germ) at
be the element (germ) at 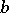 of a solution of (4), normalized by the condition
of a solution of (4), normalized by the condition 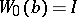 , and let
, and let 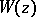 be the analytic function in
be the analytic function in 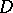 generated by this element. Then
generated by this element. Then 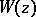 is an entire function of the matrices
is an entire function of the matrices  and has a series expansion
and has a series expansion
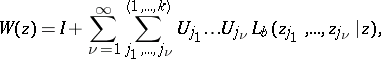 |
which converges uniformly in  on every compact set
on every compact set 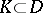 . The integral substitution
. The integral substitution 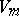 at
at 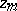 corresponding to the solution
corresponding to the solution 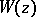 is an entire function of
is an entire function of 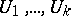 and has a series expansion
and has a series expansion
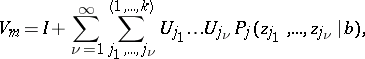 |
where 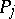 can be expressed in terms of hyperlogarithms (see [3], [6]).
can be expressed in terms of hyperlogarithms (see [3], [6]).
Formulas that give a solution to problem C) have also been obtained (see [3]).
References
| [1a] | J.L. Fuchs, "Zur Theorie der linearen Differentialgleichungen mit Veränderlichen Koeffizienten" J. Reine Angew. Math. , 66 (1866) pp. 121–160 |
| [1b] | J.L. Fuchs, "Zur Theorie der linearen Differentialgleichungen mit Veränderlichen Koeffizienten. Ergänzung" J. Reine Angew. Math. , 68 (1868) pp. 354–385 |
| [2] | H. Poincaré, "Papers on Fuchsian functions" , Springer (1985) (Translated from French) |
| [3] | I.A. Lappo-Danilevskii, "Applications des fonctions matrices dans la theorie des systèeme des équations différentielles ordinaires lineaires" , Moscow (1957) (In Russian; translated from French) |
| [4] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [5] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
| [6] | V.I. Smirnov, "A course of higher mathematics" , 3 , Addison-Wesley (1964) pp. Part 2 (Translated from Russian) |
| [7] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
Comments
The matrix 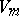 of equation (5) is also called the local monodromy at
of equation (5) is also called the local monodromy at 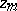 or the monodromy matrix at
or the monodromy matrix at 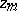 of the Fuchsian system (4). Riemann posed the problem, the Riemann monodromy problem, of finding for given
of the Fuchsian system (4). Riemann posed the problem, the Riemann monodromy problem, of finding for given 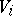 a Fuchsian system with these given monodromy matrices. This problem was essentially solved by J. Plemelj [a3], G. Birkhoff [a4], [a5] and I.A. Lappo-Danilevskii [a2]. By taking a contour
a Fuchsian system with these given monodromy matrices. This problem was essentially solved by J. Plemelj [a3], G. Birkhoff [a4], [a5] and I.A. Lappo-Danilevskii [a2]. By taking a contour 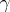 through all the
through all the 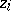 and
and 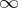 and a piecewise-constant matrix function on
and a piecewise-constant matrix function on 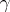 (value
(value 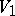 between
between 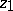 and
and 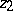 , value
, value 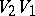 between
between 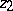 and
and 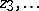 ) the problem can be turned into a Riemann–Hilbert problem. The conditions on the points
) the problem can be turned into a Riemann–Hilbert problem. The conditions on the points 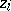 and the matrices
and the matrices  which are necessary and sufficient for the systems to retain the same monodromy under smooth changes in these parameters take the form of differential equations known as the isomonodromy equations or Schlessinger equations. These equations have links to (completely) integrable systems (cf. Integrable system) and quantum fields, cf., e.g., [a6], [a7].
which are necessary and sufficient for the systems to retain the same monodromy under smooth changes in these parameters take the form of differential equations known as the isomonodromy equations or Schlessinger equations. These equations have links to (completely) integrable systems (cf. Integrable system) and quantum fields, cf., e.g., [a6], [a7].
References
| [a1] | E. Hille, "Ordinary differential equations in the complex domain" , Wiley (1976) |
| [a2] | I.A. Lappo-Danilevskii, "Mémoire sur la théorie des systèmes des équations différentielles linéaires" , Dover, reprint (1953) |
| [a3] | J. Plemelj, "Problems in the sense of Riemann and Klein" , Wiley (1964) |
| [a4] | G.D. Birkhoff, "Singular points of ordinary linear differential equations" Trans. Amer. Math. Soc. , 10 (1909) pp. 434–470 |
| [a5] | G.D. Birkhoff, "A simplified treatment of the regular singular point" Trans. Amer. Math. Soc. , 11 (1910) pp. 199–202 |
| [a6] | D.V. Chudnovsky, "Riemann, monodromy problem, isomonodromy deformations and completely integrable systems" C. Bardos (ed.) D. Bessis (ed.) , Bifurcation phenomena in mathematical physics and related topics , Reidel (1980) pp. 385–447 |
| [a7] | M. Jimbo, T. Miwa, M. Sato, "Holonomic quantum fields—the unanticipated link between deformation theory of differential equations and quantum fields" K. Osterwalder (ed.) , Mathematical problems in theoretical physics , Springer (1980) pp. 119–142 |
Fuchsian equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fuchsian_equation&oldid=19254