Frame
A set of linearly independent vectors taken in a definite order and placed at a common origin. Any three non-parallel vectors not lying in one plane can serve as a frame for the vectors in space. If the vectors building the frame are mutually orthogonal, then the frame is called orthogonal; if in this case the length of the vectors is equal to one, the frame is called orthonormal.
Comments
Usually a frame is called a basis (of vectors in space). In this sense, the word "frame" is also used in physics (frame of reference, cf. Reference system). For Frénet frame see Frénet trihedron.
A framing of an  -dimensional differentiable manifold
-dimensional differentiable manifold  is a vector bundle isomorphism of its tangent bundle
is a vector bundle isomorphism of its tangent bundle 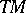 with the trivial bundle
with the trivial bundle 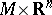 (so that
(so that  is parallelizable). Using the standard basis
is parallelizable). Using the standard basis 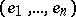 of
of 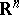 such an isomorphism defines a frame field: it assigns to every
such an isomorphism defines a frame field: it assigns to every 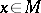 a frame, or basis, of the tangent space at that point.
a frame, or basis, of the tangent space at that point.
The frame bundle over a manifold 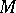 is the principal fibre bundle with structure group
is the principal fibre bundle with structure group 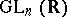 whose fibre over
whose fibre over 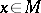 is the collection of all bases (frames) of
is the collection of all bases (frames) of 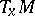 , the tangent space at that point.
, the tangent space at that point.
A 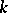 -frame
-frame 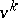 in
in 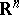 is an ordered set of
is an ordered set of 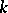 linearly independent vectors. Let
linearly independent vectors. Let 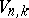 denote the set of all
denote the set of all 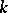 -frames in
-frames in 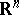 . Let
. Let  be the subgroup of
be the subgroup of 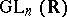 leaving a fixed frame
leaving a fixed frame 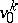 invariant. Then
invariant. Then 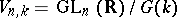 . Thus,
. Thus, 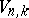 has a real-analytic structure. It is called the Stiefel manifold of
has a real-analytic structure. It is called the Stiefel manifold of 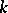 -frames in
-frames in  -space.
-space.
References
| [a1] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
Frame. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frame&oldid=16777