Formal language
in mathematical linguistics
An arbitrary set of chains (that is, words, cf. Word) over some (finite or infinite) alphabet  (sometimes also called a dictionary), that is, a set of expressions of the form
(sometimes also called a dictionary), that is, a set of expressions of the form  , where
, where  ; the number
; the number  , usually denoted by
, usually denoted by  , is the length of the chain
, is the length of the chain  . One also considers the empty chain, denoted by
. One also considers the empty chain, denoted by  ; one sets
; one sets  . One often speaks of a language over the alphabet
. One often speaks of a language over the alphabet  , omitting the word "formal" . In mathematical linguistics and the theory of automata (cf. Automata, theory of) one considers various effective ways of specifying a formal language, principally by means of formal grammars (cf. Grammar, formal) and automata of various types, which can, in the majority of cases, be described as modifications of non-deterministic Turing machines (cf. Turing machine), often multi-tape, with some restrictions on the ways the machine works on each tape.
, omitting the word "formal" . In mathematical linguistics and the theory of automata (cf. Automata, theory of) one considers various effective ways of specifying a formal language, principally by means of formal grammars (cf. Grammar, formal) and automata of various types, which can, in the majority of cases, be described as modifications of non-deterministic Turing machines (cf. Turing machine), often multi-tape, with some restrictions on the ways the machine works on each tape.
Operations on formal languages.
In addition to the usual set-theoretic operations on formal languages, one carries out: multiplication (or direct multiplication, or concatenation):
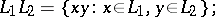 |
left division:
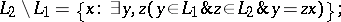 |
right division 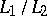 is defined by analogy with left division; iteration:
is defined by analogy with left division; iteration:
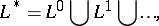 |
where  denotes
denotes  and
and  (in particular, the set of all chains in
(in particular, the set of all chains in 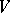 is
is  ); truncated iteration:
); truncated iteration:
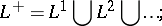 |
and substitution: If  is a language over the finite alphabet
is a language over the finite alphabet  and
and  are arbitrary languages, then
are arbitrary languages, then
 |
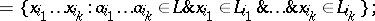 |
if each of the languages  ,
, 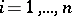 , consists of one chain
, consists of one chain  , a substitution is called a homomorphism; if all the
, a substitution is called a homomorphism; if all the 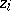 are non-empty, one speaks of an unabbreviated homomorphism. If the language
are non-empty, one speaks of an unabbreviated homomorphism. If the language 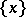 consists of one chain
consists of one chain  , then instead of
, then instead of 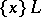 ,
, 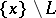 , etc., one writes
, etc., one writes 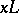 ,
,  , etc., respectively.
, etc., respectively.
A variety of languages is an ordered pair 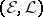 (or
(or  , if
, if 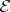 is taken for granted), where
is taken for granted), where 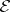 is an infinite alphabet and
is an infinite alphabet and  is a class of languages such that: 1) for every
is a class of languages such that: 1) for every  there is a finite alphabet
there is a finite alphabet  such that
such that  ; 2)
; 2)  for some
for some  ; and 3)
; and 3)  is closed relative to union, multiplication, intersection with regular sets, truncated iteration, unabbreviated homomorphisms, and inverses of arbitrary homomorphisms. A variety that is closed relative to arbitrary homomorphisms is called complete.
is closed relative to union, multiplication, intersection with regular sets, truncated iteration, unabbreviated homomorphisms, and inverses of arbitrary homomorphisms. A variety that is closed relative to arbitrary homomorphisms is called complete.
References
| [1] | A.V. Gladkii, "Formal grammars and languages" , Moscow (1973) (In Russian) |
| [2] | S. Ginsburg, S. Greibach, Y. Hopcroft, "Studies in abstract families of languages" Mem. Amer. Math. Soc. , 87 (1969) pp. 1–32 |
Comments
For more details see Formal languages and automata.
Formal language. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Formal_language&oldid=18696