Difference between revisions of "Flow (continuous-time dynamical system)"
(MSC|37-01) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f0406506.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f0406506.png" /></td> </tr></table> | ||
| − | In this case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f0406507.png" /> is usually called | + | In this case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f0406507.png" /> is usually called "time" and the dependence of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f0406508.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f0406509.png" /> (for a fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065010.png" />) is said to be the "motion" of the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065011.png" />; the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065012.png" /> for a given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065013.png" /> is called the trajectory (or orbit) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065014.png" /> (sometimes this term is used to describe the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065015.png" />). Just as for traditional dynamical systems the phase space of a flow usually is provided with a certain structure with which the flow is compatible: the transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065016.png" /> preserve this structure and certain conditions are imposed on the manner in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065017.png" /> depends on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065018.png" />. |
In applications one usually encounters flows described by autonomous systems (cf. [[Autonomous system|Autonomous system]]) of ordinary differential equations | In applications one usually encounters flows described by autonomous systems (cf. [[Autonomous system|Autonomous system]]) of ordinary differential equations | ||
| Line 13: | Line 13: | ||
or, in vector notation, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065021.png" />. The immediate generalization of a flow is a flow on a differentiable manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065022.png" /> defined ( "generated" ) by a smooth vector field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065023.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065025.png" /> (a smooth flow of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065027.png" />) given on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065028.png" />. In this case the motion of a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065029.png" />, as long as it stays within one chart (local coordinate system), is described by a system of the form (*), in the right-hand side of which one finds the components of the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065030.png" /> in the corresponding coordinates. When passing to another chart the description of the motion changes, since in this case both the coordinates of the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065031.png" /> change as well as the expressions for the components of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065032.png" /> as functions of the local coordinates. See also [[Measurable flow|Measurable flow]]; [[Continuous flow|Continuous flow]]; [[Topological dynamical system|Topological dynamical system]]. | or, in vector notation, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065021.png" />. The immediate generalization of a flow is a flow on a differentiable manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065022.png" /> defined ( "generated" ) by a smooth vector field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065023.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065025.png" /> (a smooth flow of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065027.png" />) given on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065028.png" />. In this case the motion of a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065029.png" />, as long as it stays within one chart (local coordinate system), is described by a system of the form (*), in the right-hand side of which one finds the components of the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065030.png" /> in the corresponding coordinates. When passing to another chart the description of the motion changes, since in this case both the coordinates of the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065031.png" /> change as well as the expressions for the components of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040650/f04065032.png" /> as functions of the local coordinates. See also [[Measurable flow|Measurable flow]]; [[Continuous flow|Continuous flow]]; [[Topological dynamical system|Topological dynamical system]]. | ||
| − | Flows form the most important class of dynamical systems and were, moreover, the first to be studied. The term | + | Flows form the most important class of dynamical systems and were, moreover, the first to be studied. The term "dynamical system" is often used in a narrow sense, meaning precisely a flow (or a flow and a [[Cascade|cascade]]). |
| Line 21: | Line 21: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.P. Bhatia, G.P. Szegö, "Stability theory of dynamical systems" , Springer (1970) {{MR|0289890}} {{ZBL|0213.10904}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) {{MR|832433}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Palis, W. de Melo, "Geometric theory of dynamical systems" , Springer (1982) {{MR|0669541}} {{ZBL|0491.58001}} </TD></TR></table> |
Revision as of 10:30, 27 March 2012
2020 Mathematics Subject Classification: Primary: 37-01 [MSN][ZBL]
A dynamical system determined by an action of the additive group of real numbers  (or additive semi-group of non-negative real numbers) on a phase space
(or additive semi-group of non-negative real numbers) on a phase space  . In other words, to each
. In other words, to each  (to each
(to each  ) corresponds a transformation
) corresponds a transformation  such that
such that
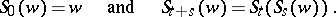 |
In this case  is usually called "time" and the dependence of
is usually called "time" and the dependence of  on
on 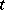 (for a fixed
(for a fixed 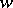 ) is said to be the "motion" of the point
) is said to be the "motion" of the point 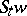 ; the set of all
; the set of all 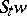 for a given
for a given 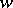 is called the trajectory (or orbit) of
is called the trajectory (or orbit) of 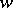 (sometimes this term is used to describe the function
(sometimes this term is used to describe the function 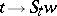 ). Just as for traditional dynamical systems the phase space of a flow usually is provided with a certain structure with which the flow is compatible: the transformations
). Just as for traditional dynamical systems the phase space of a flow usually is provided with a certain structure with which the flow is compatible: the transformations 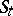 preserve this structure and certain conditions are imposed on the manner in which
preserve this structure and certain conditions are imposed on the manner in which 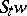 depends on
depends on 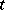 .
.
In applications one usually encounters flows described by autonomous systems (cf. Autonomous system) of ordinary differential equations
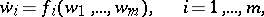 | (*) |
or, in vector notation, 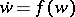 ,
, 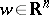 . The immediate generalization of a flow is a flow on a differentiable manifold
. The immediate generalization of a flow is a flow on a differentiable manifold 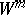 defined ( "generated" ) by a smooth vector field
defined ( "generated" ) by a smooth vector field 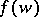 of class
of class 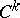 ,
, 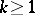 (a smooth flow of class
(a smooth flow of class 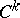 ) given on
) given on 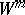 . In this case the motion of a point
. In this case the motion of a point 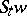 , as long as it stays within one chart (local coordinate system), is described by a system of the form (*), in the right-hand side of which one finds the components of the vector
, as long as it stays within one chart (local coordinate system), is described by a system of the form (*), in the right-hand side of which one finds the components of the vector 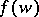 in the corresponding coordinates. When passing to another chart the description of the motion changes, since in this case both the coordinates of the point
in the corresponding coordinates. When passing to another chart the description of the motion changes, since in this case both the coordinates of the point 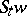 change as well as the expressions for the components of
change as well as the expressions for the components of 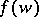 as functions of the local coordinates. See also Measurable flow; Continuous flow; Topological dynamical system.
as functions of the local coordinates. See also Measurable flow; Continuous flow; Topological dynamical system.
Flows form the most important class of dynamical systems and were, moreover, the first to be studied. The term "dynamical system" is often used in a narrow sense, meaning precisely a flow (or a flow and a cascade).
Comments
For general introductions into the theory of continuous, measurable or smooth flows, consult, respectively, [a1], [a2] and [a3].
References
| [a1] | N.P. Bhatia, G.P. Szegö, "Stability theory of dynamical systems" , Springer (1970) MR0289890 Zbl 0213.10904 |
| [a2] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) MR832433 |
| [a3] | J. Palis, W. de Melo, "Geometric theory of dynamical systems" , Springer (1982) MR0669541 Zbl 0491.58001 |
Flow (continuous-time dynamical system). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flow_(continuous-time_dynamical_system)&oldid=21160