Difference between revisions of "Filter"
(More precise on neighbourhood filter) |
m (link) |
||
| Line 9: | Line 9: | ||
The set of all filters over a given set is partially ordered by inclusion. A maximal element of it is called an ultrafilter (a maximal proper filter in any Boolean algebra is also called an ultrafilter). | The set of all filters over a given set is partially ordered by inclusion. A maximal element of it is called an ultrafilter (a maximal proper filter in any Boolean algebra is also called an ultrafilter). | ||
| − | Examples of filters. 1) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013022.png" /> be the subset of the natural numbers consisting of those numbers that are multiples of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013023.png" />; the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013024.png" /> is a filter base; the filter spanned by this base consists of those subsets that contain some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013025.png" />. 2) The collection of all subsets containing a certain fixed non-empty subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013026.png" /> is a filter over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013027.png" />, called a principal filter. All filters over a finite set are principal. 3) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013028.png" /> is an infinite set of cardinality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013030.png" /> is the collection of all subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013031.png" /> whose complements have cardinality less than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013032.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013033.png" /> is a filter (called a Fréchet filter). A Fréchet filter is an example of a non-principal filter. 4) The system of subsets containing some fixed point of a set is also a filter; moreover, it is an ultrafilter. 5) Suppose a topology is given on $E$; then the [[neighbourhood]]s of any point $x \in E$ (the subsets of $E$ containing $x$ in the interior) form a filter. | + | Examples of filters. 1) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013022.png" /> be the subset of the natural numbers consisting of those numbers that are multiples of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013023.png" />; the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013024.png" /> is a filter base; the filter spanned by this base consists of those subsets that contain some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013025.png" />. 2) The collection of all subsets containing a certain fixed non-empty subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013026.png" /> is a filter over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013027.png" />, called a principal filter. All filters over a finite set are principal. 3) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013028.png" /> is an infinite set of cardinality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013030.png" /> is the collection of all subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013031.png" /> whose complements have cardinality less than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013032.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040130/f04013033.png" /> is a filter (called a [[Fréchet filter]]). A Fréchet filter is an example of a non-principal filter. 4) The system of subsets containing some fixed point of a set is also a filter; moreover, it is an ultrafilter. 5) Suppose a topology is given on $E$; then the [[neighbourhood]]s of any point $x \in E$ (the subsets of $E$ containing $x$ in the interior) form a filter. |
====References==== | ====References==== | ||
Revision as of 06:34, 25 September 2017
dual ideal
A non-empty subset  of a partially ordered set
of a partially ordered set  satisfying the conditions: a) if
satisfying the conditions: a) if  and if the infimum
and if the infimum  exists, then
exists, then  ; and b) if
; and b) if  and
and  , then
, then  . The concept of a filter is dual to that of an ideal of a partially ordered set.
. The concept of a filter is dual to that of an ideal of a partially ordered set.
A filter over a non-empty set  (or in a set
(or in a set  ) is a proper filter of the set of subsets of
) is a proper filter of the set of subsets of 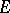 , ordered by inclusion i.e. any non-empty collection
, ordered by inclusion i.e. any non-empty collection 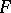 of subsets of
of subsets of 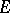 satisfying the conditions: If
satisfying the conditions: If  , then
, then  ; if
; if 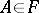 and
and 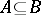 , then
, then 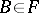 ; the empty set does not belong to
; the empty set does not belong to 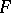 .
.
A filter base is a system of subsets of 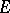 satisfying the two conditions: 1) the empty set does not belong to it; and 2) the intersection of two subsets belonging to it contains some third subset belonging to it. Every filter is completely determined by any of its filter bases. The system of all subsets of
satisfying the two conditions: 1) the empty set does not belong to it; and 2) the intersection of two subsets belonging to it contains some third subset belonging to it. Every filter is completely determined by any of its filter bases. The system of all subsets of 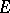 that contain some element of a given filter base is a filter. It is said to be spanned by this base.
that contain some element of a given filter base is a filter. It is said to be spanned by this base.
The set of all filters over a given set is partially ordered by inclusion. A maximal element of it is called an ultrafilter (a maximal proper filter in any Boolean algebra is also called an ultrafilter).
Examples of filters. 1) Let 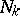 be the subset of the natural numbers consisting of those numbers that are multiples of
be the subset of the natural numbers consisting of those numbers that are multiples of 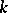 ; the system
; the system 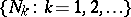 is a filter base; the filter spanned by this base consists of those subsets that contain some
is a filter base; the filter spanned by this base consists of those subsets that contain some 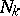 . 2) The collection of all subsets containing a certain fixed non-empty subset
. 2) The collection of all subsets containing a certain fixed non-empty subset 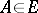 is a filter over
is a filter over 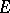 , called a principal filter. All filters over a finite set are principal. 3) If
, called a principal filter. All filters over a finite set are principal. 3) If 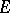 is an infinite set of cardinality
is an infinite set of cardinality 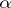 and
and 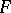 is the collection of all subsets of
is the collection of all subsets of  whose complements have cardinality less than
whose complements have cardinality less than 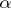 , then
, then 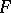 is a filter (called a Fréchet filter). A Fréchet filter is an example of a non-principal filter. 4) The system of subsets containing some fixed point of a set is also a filter; moreover, it is an ultrafilter. 5) Suppose a topology is given on $E$; then the neighbourhoods of any point $x \in E$ (the subsets of $E$ containing $x$ in the interior) form a filter.
is a filter (called a Fréchet filter). A Fréchet filter is an example of a non-principal filter. 4) The system of subsets containing some fixed point of a set is also a filter; moreover, it is an ultrafilter. 5) Suppose a topology is given on $E$; then the neighbourhoods of any point $x \in E$ (the subsets of $E$ containing $x$ in the interior) form a filter.
References
| [1] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [2] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [3] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
Comments
There is some disagreement about the definition of a filter in a partially ordered set where finite infima do not always exist. Most authors would replace condition a) in the first paragraph above by "if a, b F, then there exists a c F with c≤ a and c≤ b" , cf. [a1]. This avoids some rather pathological seeming cases.
A further meaning of the word "filter" occurs in the theory of (partially observed) stochastic processes, cf. Stochastic processes, filtering of.
References
| [a1] | K. Kunen, "Set theory" , North-Holland (1980) |
Filter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Filter&oldid=30577