Figà-Talamanca algebra
Let 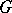 be a locally compact group,
be a locally compact group, 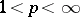 and
and 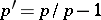 . Consider the set
. Consider the set 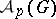 of all pairs
of all pairs 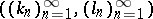 , with
, with 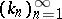 a sequence in
a sequence in 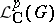 and
and 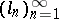 a sequence in
a sequence in  such that
such that 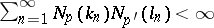 . Here,
. Here, 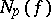 is defined by
is defined by 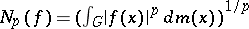 , where
, where  is some left-invariant Haar measure on
is some left-invariant Haar measure on 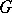 . Let
. Let 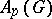 denote the set of all
denote the set of all 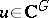 for which there is a pair
for which there is a pair  such that
such that  , where
, where  . The set
. The set 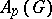 is a linear subspace of the
is a linear subspace of the 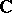 -vector space of all continuous complex-valued functions on
-vector space of all continuous complex-valued functions on 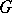 vanishing at infinity. For
vanishing at infinity. For  one sets
one sets
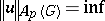 |
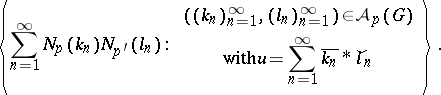 |
1) For the pointwise product on 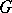 ,
, 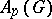 is a Banach algebra. This algebra is called the Figà-Talamanca algebra of
is a Banach algebra. This algebra is called the Figà-Talamanca algebra of 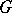 . If
. If 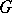 is Abelian,
is Abelian, 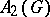 is isometrically isomorphic to
is isometrically isomorphic to  , where
, where 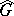 is the dual group of
is the dual group of 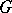 . For
. For 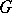 not necessarily Abelian,
not necessarily Abelian, 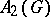 is precisely the Fourier algebra of
is precisely the Fourier algebra of 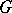 .
.
2) If 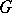 is amenable, then
is amenable, then 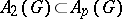 . The algebra
. The algebra  is a useful tool for studying the
is a useful tool for studying the 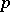 -convolution operators of
-convolution operators of 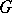 (see [a2], [a7], [a8]). For a function
(see [a2], [a7], [a8]). For a function 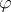 on
on 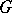 and
and 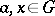 one sets
one sets 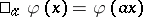 . A continuous linear operator
. A continuous linear operator 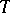 on
on 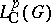 is said to be a
is said to be a 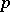 -convolution operator of
-convolution operator of  if
if 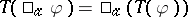 for every
for every 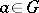 and every
and every 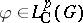 . Let
. Let 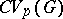 be the set of all
be the set of all 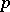 -convolution operators of
-convolution operators of 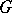 . It is a closed subalgebra of the Banach algebra
. It is a closed subalgebra of the Banach algebra 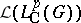 of all continuous linear operators on
of all continuous linear operators on 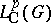 . For a complex bounded measure
. For a complex bounded measure 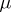 on
on 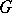 (i.e.
(i.e. 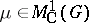 ) and a continuous complex-valued function
) and a continuous complex-valued function 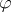 with compact support on
with compact support on 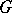 (
(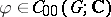 ), the rule
), the rule 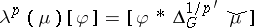 defines a
defines a  -convolution operator
-convolution operator 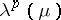 . Of course, for
. Of course, for 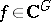 ,
, 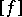 denotes the set of all
denotes the set of all 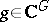 with
with 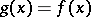
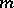 -almost everywhere.
-almost everywhere.
Even for 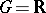 one has
one has 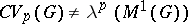 . Let
. Let 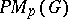 be the closure in
be the closure in 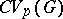 of
of 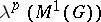 with respect to the ultraweak operator topology on
with respect to the ultraweak operator topology on 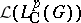 .
.
3) The dual 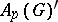 of the Banach space
of the Banach space 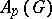 is canonically isometrically isomorphic to
is canonically isometrically isomorphic to 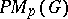 . Also,
. Also, 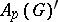 with the topology
with the topology 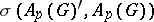 is homeomorphic to
is homeomorphic to 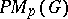 with the ultraweak operator topology on
with the ultraweak operator topology on 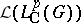 . As a consequence, for
. As a consequence, for 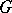 amenable or for
amenable or for 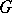 arbitrary but with
arbitrary but with 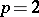 ,
, 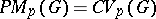 .
.
This duality between  and
and 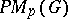 also permits one to develop (see [a1]) a kind of "non-commutative harmonic analysis on G" , where (for
also permits one to develop (see [a1]) a kind of "non-commutative harmonic analysis on G" , where (for 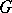 Abelian)
Abelian) 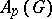 replaces
replaces 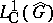 and
and 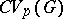 replaces
replaces 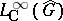 . (Cf. also Harmonic analysis, abstract.)
. (Cf. also Harmonic analysis, abstract.)
Let 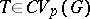 . Then the support of
. Then the support of 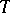 , denoted by
, denoted by 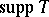 , is the set of all
, is the set of all 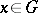 for which for all open subsets
for which for all open subsets 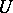 ,
, 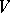 , of
, of  with
with 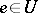 and
and 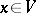 there are
there are 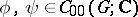 with
with 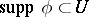 ,
, 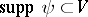 and
and
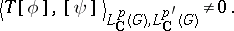 |
If 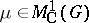 , then
, then 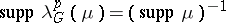 . For
. For  Abelian, let
Abelian, let  be the canonical mapping from
be the canonical mapping from  onto
onto 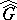 . Then
. Then 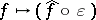 , where
, where 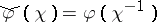 , is an isometric isomorphism of the Banach algebra
, is an isometric isomorphism of the Banach algebra 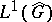 onto
onto 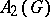 . Let
. Let  and
and 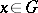 . Then
. Then  "belongs to the spectrum of u" (written as
"belongs to the spectrum of u" (written as 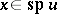 ) if
) if 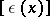 lies in the closure of the linear span of
lies in the closure of the linear span of 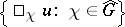 in
in 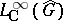 , for the weak topology
, for the weak topology 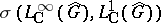 . Let
. Let 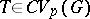 ; then
; then 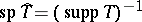 . For
. For 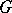 not necessarily amenable and
not necessarily amenable and 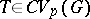 ,
, 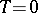 if and only
if and only 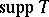 is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for
is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for 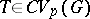 ,
, 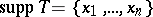 if and only there exist
if and only there exist 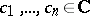 such that
such that 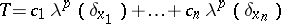 , where
, where 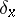 denotes the Dirac measure in
denotes the Dirac measure in  (cf. also Dirac distribution). In fact, even for
(cf. also Dirac distribution). In fact, even for 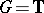 or for
or for 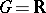 (but
(but 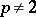 ) the situation is not classical!
) the situation is not classical!
The Banach space 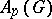 has been first introduced by A. Figà-Talamanca in [a3] for
has been first introduced by A. Figà-Talamanca in [a3] for 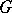 Abelian or
Abelian or 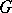 non-Abelian but compact. For these classes of groups he obtained assertion 3) above. The statement for a general locally compact group is due to C.S. Herz [a5]. Assertion 1) is also due to Herz [a4].
non-Abelian but compact. For these classes of groups he obtained assertion 3) above. The statement for a general locally compact group is due to C.S. Herz [a5]. Assertion 1) is also due to Herz [a4].
The Banach algebra 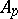 also satisfies the following properties:
also satisfies the following properties:
a) Let 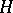 be a closed subgroup of
be a closed subgroup of 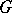 . Then
. Then 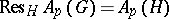 . More precisely, for every
. More precisely, for every 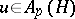 and for every
and for every 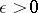 there is a
there is a 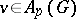 with
with 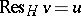 and
and 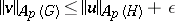 (see [a5]).
(see [a5]).
b) The Banach algebra 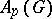 has bounded approximate units (i.e. there is a
has bounded approximate units (i.e. there is a 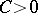 such that for every
such that for every  and for every
and for every 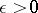 there is a
there is a  with
with 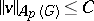 and
and 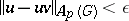 ) if and only if the locally compact group
) if and only if the locally compact group 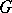 is amenable (see [a5] and [a6] for
is amenable (see [a5] and [a6] for 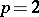 ). This algebra is often called the Figà-Talamanca–Herz algebra.
). This algebra is often called the Figà-Talamanca–Herz algebra.
See also Fourier algebra.
References
| [a1] | A. Derighetti, "Quelques observations concernant les ensembles de Ditkin d'un groupe localement compact" Monatsh. Math. , 101 (1986) pp. 95–113 |
| [a2] | P. Eymard, "Algèbres 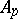 et convoluteurs de et convoluteurs de 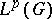 " , Sem. Bourbaki 1969/70, Exp. 367 , Lecture Notes in Math. , 180 , Springer (1971) pp. 364–381 " , Sem. Bourbaki 1969/70, Exp. 367 , Lecture Notes in Math. , 180 , Springer (1971) pp. 364–381 |
| [a3] | A. Figà-Talamanca, "Translation invariant operators in 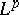 " Duke Math. J. , 32 (1965) pp. 495–501 " Duke Math. J. , 32 (1965) pp. 495–501 |
| [a4] | C. Herz, "The theory of 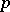 -spaces" Trans. Amer. Math. Soc. , 154 (1971) pp. 69–82 -spaces" Trans. Amer. Math. Soc. , 154 (1971) pp. 69–82 |
| [a5] | C. Herz, "Harmonic synthesis for subgroups" Ann. Inst. Fourier (Grenoble) , 23 : 3 (1973) pp. 91–123 |
| [a6] | H. Leptin, "Sur l'algèbre de Fourier d'un groupe localement compact" C.R. Acad. Sci. Paris Sér. A , 266 (1968) pp. 1180–1182 |
| [a7] | N. Lohoué, "Algèbres 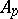 et convoluteurs de et convoluteurs de 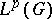 " Thèse, Univ. Paris-Sud (1971) " Thèse, Univ. Paris-Sud (1971) |
| [a8] | N. Lohoué, "Estimations 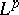 des coefficients de représentations et opérateurs de convolution" Adv. Math. , 38 (1980) pp. 178–221 des coefficients de représentations et opérateurs de convolution" Adv. Math. , 38 (1980) pp. 178–221 |
| [a9] | J.R. McMullen, "Extensions of positive-definite functions" Memoirs Amer. Math. Soc. , 117 (1972) |
| [a10] | J.-P. Pier, "Amenable locally compact groups" , Wiley (1984) |
Figà-Talamanca algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fig%C3%A0-Talamanca_algebra&oldid=18073