F-algebra

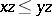A real vector space that is simultaneously a lattice is called a vector lattice (or Riesz space) whenever ( is the lattice order) implies for all and for all positive real numbers . If is also an algebra and and for all , the positive cone of , then is called an -algebra (a lattice-ordered algebra, Riesz algebra).

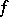A Riesz algebra is called an -algebra ( for "function" ) whenever

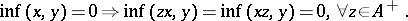This notion was introduced by G. Birkhoff and R.S. Pierce in 1956.

An important example of an -algebra is , the space of continuous functions (cf. Continuous functions, space of) on some topological space . Other examples are spaces of Baire functions, measurable functions and essentially bounded functions. -Algebras play an important role in operator theory. The second commutant of a commuting subset of bounded Hermitian operators on some Hilbert space is an -algebra. A linear operator on some vector lattice is called an orthomorphism whenever 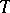is the difference of two positive orthomorphisms; a positive orthomorphism 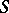on leaves the positive cone of invariant and satisfies whenever . The space 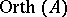of all orthomorphisms of is an important example of an 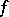-algebra in the theory of vector lattices.

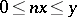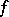A vector lattice is termed Archimedean if () implies . Archimedean -algebras are automatically commutative and associative. An Archimedean -algebra with unit element is semi-prime (i.e., the only nilpotent element is ). The latter two properties are nice examples of the interplay between order properties and algebraic properties in an -algebra. Many properties of are inherited by an -algebra 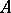with a unit element (under some additional completeness condition), such as the existence of the square root of a positive element (if 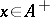, then there exists a unique 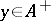such that 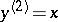) and the existence of an inverse: if is the unit element of and 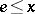, then exists in .

References

[a1]	G. Birkhoff, R.S. Pierce, "Lattice-ordered rings" An. Acad. Brasil. Ci. , 28 (1956) pp. 41–69
[a2]	A.C. Zaanen, "Riesz spaces" , II , North-Holland (1983)