Evolute
of a plane curve
The set $ \widetilde \gamma $ of the centres of curvature of the given curve $ \gamma $. If $ \mathbf r = \mathbf r ( s) $( where $ s $ is the arc length parameter of $ \gamma $) is the equation of $ \gamma $, then the equation of its evolute has the form
$$ \widetilde{\mathbf r} = \mathbf r + \frac{1}{k} {\pmb\nu } , $$
where $ k $ is the curvature and $ {\pmb\nu } $ the unit normal to $ \gamma $. The figures shows the construction of the evolute in three typical cases:
a) if along the entire curve $ k ^ \prime $ has a fixed sign and $ k $ does not vanish;
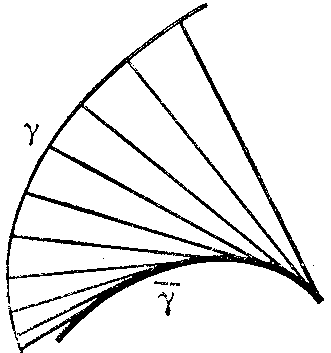
Figure: e036670a
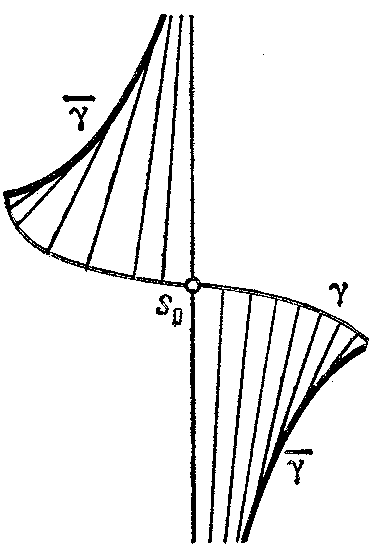
Figure: e036670b
b) if along the entire curve $ k ^ \prime $ has a fixed sign and $ k $ vanishes for $ s = s _ {0} $; and
c) if $ k ^ \prime > 0 $ for $ s < s _ {0} $; $ k ^ \prime ( s) < 0 $ for $ s > s _ {0} $; $ k ^ \prime ( s _ {0} ) = 0 $, and $ k $ does not vanish (the point of the evolute corresponding to $ s = s _ {0} $ is a cusp).
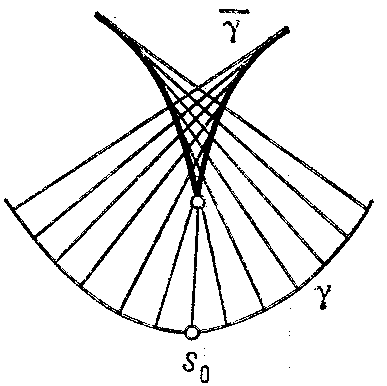
Figure: e036670c
The length of the arc of the evolute corresponding to the segment $ s _ {1} \leq s \leq s _ {2} $ of $ \gamma $ is
$$ \widetilde{s} ( s _ {1} , s _ {2} ) = \left | \frac{1}{k ( s _ {2} ) } - \frac{1}{k ( s _ {1} ) } \right | . $$
The evolute is the envelope of the normals to $ \gamma $. The curve $ \gamma $ is called the evolvent of its evolute (cf. Evolvent of a plane curve).
Comments
The evolvent is also called the involute; thus, if $ \gamma ^ \prime $ is the evolute of $ \gamma $, then $ \gamma $ is the involute of $ \gamma ^ \prime $, cf. Evolvent of a plane curve.
References
| [a1] | H.-R. Müller, "Kinematik" , de Gruyter (1963) |
| [a2] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. 305 (Translated from French) |
| [a3] | J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) pp. 195 |
| [a4] | M. Berger, "Geometry" , I , Springer (1987) pp. 253–254 |
| [a5] | H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60 |
Evolute. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Evolute&oldid=46863