Ernst equation
In an oriented space-time with a time-like Killing vector field 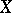 , the twist
, the twist 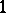 -form
-form  is defined by
is defined by
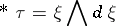 |
where 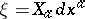 . It is always closed in vacuum solutions to the Einstein gravitational equations; that is, when the Ricci tensor
. It is always closed in vacuum solutions to the Einstein gravitational equations; that is, when the Ricci tensor 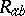 vanishes.
vanishes.
In such space-times, one can write (locally) 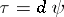 , where
, where 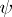 is constant along
is constant along 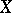 . The Ernst potential is the complex quantity
. The Ernst potential is the complex quantity 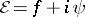 , where
, where 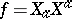 and
and 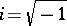 . It is used in a number of different ways in finding explicit solutions to Einstein's equations (cf. also Einstein equations; [a8] provides a wide-ranging introduction to the most of the original work on this subject).
. It is used in a number of different ways in finding explicit solutions to Einstein's equations (cf. also Einstein equations; [a8] provides a wide-ranging introduction to the most of the original work on this subject).
One use is in the generation of new solutions with one Killing vector from a known one. The idea here is to use 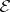 and the metric
and the metric 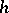 on the quotient space by the Killing vector action as dependent variables (both are functions of three variables). The vacuum equations for the space-time metric can then be derived from the action
on the quotient space by the Killing vector action as dependent variables (both are functions of three variables). The vacuum equations for the space-time metric can then be derived from the action
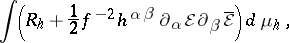 |
where 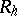 and
and 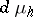 are the scalar curvature and the volume element of the
are the scalar curvature and the volume element of the  -metric
-metric 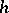 . There is a straightforward extension to the Einstein–Maxwell equations.
. There is a straightforward extension to the Einstein–Maxwell equations.
The symmetries of the action and its electro-magnetic generalization allow transformations of the solution that preserve 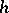 , but change the potential. They include solution-generation transformations discussed in [a6], [a7].
, but change the potential. They include solution-generation transformations discussed in [a6], [a7].
A second use is in finding stationary axi-symmetric gravitational fields (or by a straightforward modification to the formalism, solutions with other symmetries representing, for example, cylindrically symmetric gravitational waves and the interaction of colliding plane waves). Here one assumes the existence a second Killing vector 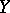 such that
such that 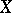 and
and 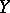 together generate a
together generate a  -dimensional Lie algebra of infinitesimal isometries. In this case, there are two twist
-dimensional Lie algebra of infinitesimal isometries. In this case, there are two twist 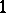 -forms. Their inner products with the Killing vectors are constant when
-forms. Their inner products with the Killing vectors are constant when 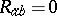 , and vanish if some combination of the Killing vectors has a fixed point.
, and vanish if some combination of the Killing vectors has a fixed point.
When they do vanish, the space-time metric can be written in the Weyl canonical form
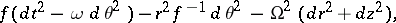 |
where  and
and 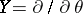 . In this case, the Ernst potential associated with
. In this case, the Ernst potential associated with 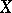 is a function of
is a function of  and
and  alone, and the vacuum equations reduce to the Ernst equation
alone, and the vacuum equations reduce to the Ernst equation
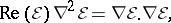 |
where  is the gradient in the three-dimensional Euclidean space on which
is the gradient in the three-dimensional Euclidean space on which  ,
, 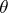 ,
,  are cylindrical polar coordinates [a4]. Once
are cylindrical polar coordinates [a4]. Once 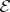 is known,
is known,  is found by quadrature. Again, there is a straightforward extension to the Einstein–Maxwell case [a5].
is found by quadrature. Again, there is a straightforward extension to the Einstein–Maxwell case [a5].
Although still non-linear, this reduction to a single scalar equation in Euclidean space for the complex potential  is a great simplification of the original vacuum equations
is a great simplification of the original vacuum equations 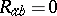 . It has been widely exploited in the search for exact solutions. In particular, the solution-generation techniques provide a rich source of new solutions since one can combine the transformations of a metric with one Killing vector with linear transformations in the Lie algebra spanned by
. It has been widely exploited in the search for exact solutions. In particular, the solution-generation techniques provide a rich source of new solutions since one can combine the transformations of a metric with one Killing vector with linear transformations in the Lie algebra spanned by 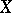 and
and 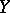 .
.
Although it is non-linear, the Ernst equation is integrable, and its transformation properties can be seen as part of the wider theory of integrable systems (cf. also Integrable system); some of the connections are explained in [a3]. One can understand them from another point of view through the observation [a2] that the Ernst equation is identical to a form of the self-dual Yang–Mills equation (cf. also Yang–Mills field) for static axi-symmetric gauge fields. If one writes
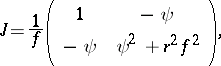 |
then the Ernst equation is equivalent to
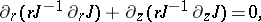 |
which is a symmetry reduction of the Yang equation. Solutions can therefore be found by solving a Riemann–Hilbert problem [a10], and, more generally, by the twistor methods reviewed in [a9].
The space-time metric gives rise to a solution of this same equation in another way by writing
 |
The mapping 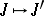 is a discrete symmetry of the reduction of Yang's equation, and many of the solution transformations can be obtained by combining it with
is a discrete symmetry of the reduction of Yang's equation, and many of the solution transformations can be obtained by combining it with 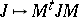 ,
,  for constant matrices
for constant matrices 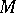 and
and 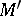 . In [a1], these are seen to generate the action of a loop group (in fact a central extension when the action on the conformal factor
. In [a1], these are seen to generate the action of a loop group (in fact a central extension when the action on the conformal factor  is included).
is included).
References
| [a1] | P. Breitenlohner, D. Maison, "On the Geroch group" Ann. Inst. H. Poincaré Phys. Th. , 46 (1987) pp. 215–46 |
| [a2] | L. Witten, "Static axially symmetric solutions of self-dual 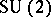 gauge fields in Euclidean four-dimensional space" Phys. Rev. , D19 (1979) pp. 718–20 gauge fields in Euclidean four-dimensional space" Phys. Rev. , D19 (1979) pp. 718–20 |
| [a3] | C. Cosgrove, "Relationships between group-theoretic and soliton-theoretic techniques for generating stationary axisymmetric gravitational solutions" J. Math. Phys. , 21 (1980) pp. 2417–47 |
| [a4] | F. Ernst, "New formulation of the axially symmetric gravitational field problem" Phys. Rev. , 167 (1968) pp. 1175–8 |
| [a5] | F. Ernst, "New formulation of the axially symmetric gravitational field problem. II" Phys. Rev. , 168 (1968) pp. 1415–17 |
| [a6] | R. Geroch, "A method for generating solutions of Einstein's equations" J. Math. Phys. , 12 (1971) pp. 918–24 |
| [a7] | W. Kinnersley, "Recent progress in exact solutions" G. Shaviv (ed.) and J. Rosen (ed.) , General Relativity and Gravitation , Wiley (1975) |
| [a8] | D. Kramer, H. Stephani, M. MacCallum, E. Herlt, "Exact solutions of Einstein's field equations" , Cambridge Univ. Press (1980) |
| [a9] | L. Mason, N. Woodhouse, "Integrability, self-duality, and twistor theory" , Oxford Univ. Press (1996) |
| [a10] | R. Ward, "Stationary axisymmetric space-times: a new approach" Gen. Rel. Grav. , 15 (1983) pp. 105–9 |
Ernst equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ernst_equation&oldid=14466