Elliptic surface
An algebraic or analytic complete non-singular surface 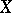 having a fibration of elliptic curves (cf. Elliptic curve), that is, a morphism
having a fibration of elliptic curves (cf. Elliptic curve), that is, a morphism 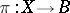 onto a non-singular curve
onto a non-singular curve 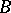 whose generic fibre is a non-singular elliptic curve. Every elliptic surface is birationally (bimeromorphically) equivalent over
whose generic fibre is a non-singular elliptic curve. Every elliptic surface is birationally (bimeromorphically) equivalent over 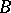 to a unique minimal model, which is characterized by the fact that the fibre of
to a unique minimal model, which is characterized by the fact that the fibre of  does not contain exceptional curves of arithmetic genus 1. In what follows an elliptic surface is assumed to be minimal. Minimal elliptic surfaces have a more complicated structure than ruled surfaces. They can have singular fibres
does not contain exceptional curves of arithmetic genus 1. In what follows an elliptic surface is assumed to be minimal. Minimal elliptic surfaces have a more complicated structure than ruled surfaces. They can have singular fibres  (that is, fibres that are not non-singular elliptic curves). There is a classification
(that is, fibres that are not non-singular elliptic curves). There is a classification
of the singular fibres of elliptic surfaces. A singular fibre 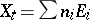 is called multiple if the greatest common divisor of the
is called multiple if the greatest common divisor of the  is
is  , and then
, and then 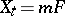 and
and 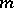 is called the multiplicity of the fibre
is called the multiplicity of the fibre 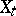 .
.
On a minimal elliptic surface the canonical class 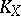 contains a divisor that is a rational combination of fibres, in particular,
contains a divisor that is a rational combination of fibres, in particular, 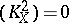 . Moreover, the following formula holds for the canonical class (see [1], ):
. Moreover, the following formula holds for the canonical class (see [1], ):
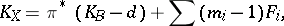 |
where 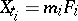 are all the multiple fibres of
are all the multiple fibres of 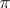 and
and 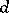 is a divisor on
is a divisor on  of degree
of degree 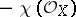 . The topological Euler characteristic satisfies the formula
. The topological Euler characteristic satisfies the formula
 |
The classification of elliptic fibrations.
A fibration  can be regarded as an elliptic curve over the function field
can be regarded as an elliptic curve over the function field  . This curve, generally speaking, does not have the structure of an Abelian variety over
. This curve, generally speaking, does not have the structure of an Abelian variety over  . For this to happen it is necessary that it has a rational point over
. For this to happen it is necessary that it has a rational point over  (and then
(and then  is birationally isomorphic to the surface defined in
is birationally isomorphic to the surface defined in 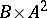 by the Weierstrass equation
by the Weierstrass equation 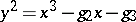 , where
, where 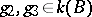 ). The specification of a rational point is equivalent to that of a section
). The specification of a rational point is equivalent to that of a section 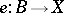 such that
such that  ; a necessary condition for the existence of a section is the absence of multiple fibres. Fibrations without multiple fibres are called reduced. Every fibration, after a suitable ramified covering of the base, has a section (that is, is reduced) . Every fibration can also be made reduced by a sequence of transformations inverse to logarithmic ones
; a necessary condition for the existence of a section is the absence of multiple fibres. Fibrations without multiple fibres are called reduced. Every fibration, after a suitable ramified covering of the base, has a section (that is, is reduced) . Every fibration can also be made reduced by a sequence of transformations inverse to logarithmic ones
— local surgery of the fibration in neighbourhoods of fibres.
Reduced elliptic fibrations may be described as follows. To every such fibration 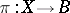 corresponds a unique fibration
corresponds a unique fibration 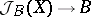 that is a group object and is such that
that is a group object and is such that 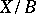 is a principal homogeneous space over
is a principal homogeneous space over  ;
;  is the Jacobi fibration for
is the Jacobi fibration for 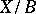 ; it characterizes the existence of a section. For a given Jacobi fibration
; it characterizes the existence of a section. For a given Jacobi fibration 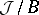 , the set
, the set 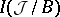 of isomorphism classes of fibrations
of isomorphism classes of fibrations 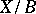 for which
for which  has a cohomology description analogous to that of invertible sheaves (cf. Invertible sheaf). Here the role of
has a cohomology description analogous to that of invertible sheaves (cf. Invertible sheaf). Here the role of 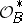 is played by the sheaf
is played by the sheaf  of local sections
of local sections  . There is a natural one-to-one correspondence
. There is a natural one-to-one correspondence
 |
under which the Jacobi fibration corresponds to the zero element. By means of  one can distinguish between algebraic and non-algebraic fibrations: For a reduced fibration
one can distinguish between algebraic and non-algebraic fibrations: For a reduced fibration  the surface
the surface  is algebraic if and only if the element corresponding to it in
is algebraic if and only if the element corresponding to it in  is of finite order. The analogy with invertible sheaves can be pursued further. The analogue of the exact sequence
is of finite order. The analogy with invertible sheaves can be pursued further. The analogue of the exact sequence
 |
is the exact sequence
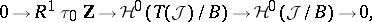 |
where  is the sheaf of local sections of the bundle
is the sheaf of local sections of the bundle  and
and 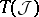 is the tangent space to the fibre
is the tangent space to the fibre  at
at  . The boundary homomorphism
. The boundary homomorphism
 |
allows one to recognize when one fibration is a deformation of another. For that it is necessary and sufficient that the elements corresponding to these fibrations have one and the same image under  (see ).
(see ).
The classification of algebraic elliptic surfaces.
Suppose that  . For an elliptic surface
. For an elliptic surface 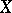 the canonical dimension
the canonical dimension 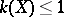 , that is, it is equal to
, that is, it is equal to 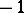 , 0 or
, 0 or  . If
. If 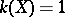 ,
,  is said to be an elliptic surface of general type. These are characterized by the conditions
is said to be an elliptic surface of general type. These are characterized by the conditions  and
and  . Elliptic surfaces with
. Elliptic surfaces with  or, more generally, with
or, more generally, with  for some
for some  , are of general type.
, are of general type.
Elliptic surfaces with  are characterized by the condition
are characterized by the condition  . In this case
. In this case 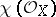 can take the three values 2, 1 or
can take the three values 2, 1 or  . If
. If  , then
, then  is an elliptic
is an elliptic 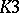 -surface (
-surface (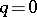 ,
,  ). In this case
). In this case  is isomorphic to the projective line
is isomorphic to the projective line 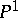 , the fibration has no multiple fibres and
, the fibration has no multiple fibres and  has the invariants
has the invariants  ,
,  ,
,  . If
. If  , then
, then  is an Enriques surface, that is, a surface with
is an Enriques surface, that is, a surface with 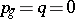 ,
,  . (Every Enriques surface is elliptic.) In this case
. (Every Enriques surface is elliptic.) In this case 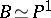 , the fibration has two fibres of multiplicity 2, and
, the fibration has two fibres of multiplicity 2, and  has the invariants
has the invariants  ,
,  . If
. If  , then two cases are possible. Either
, then two cases are possible. Either  is an Abelian variety (and then
is an Abelian variety (and then  ,
,  ,
,  ); or
); or  is a hyper-elliptic surface, that is, a surface that has a finite unramified covering — the product of two elliptic curves. In that case
is a hyper-elliptic surface, that is, a surface that has a finite unramified covering — the product of two elliptic curves. In that case 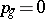 ,
,  ,
, 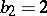 ,
, 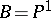 , and
, and 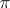 has 3 or 4 multiple fibres with four possibilities for their multiplicity:
has 3 or 4 multiple fibres with four possibilities for their multiplicity: 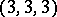 ,
,  ,
, 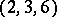 , and
, and 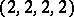 , and
, and 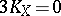 ,
, 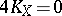 ,
, 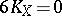 , and
, and 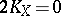 , respectively.
, respectively.
An elliptic surface with 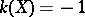 is ruled (cf. Ruled surface). It is characterized by the condition
is ruled (cf. Ruled surface). It is characterized by the condition 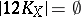 . Here two cases are possible: 1)
. Here two cases are possible: 1) 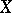 is a surface with
is a surface with 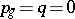 ,
, 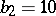 , and
, and 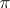 has no multiple fibres or one; moreover, a surface without multiple fibres can be obtained as follows: one has to take a rational mapping
has no multiple fibres or one; moreover, a surface without multiple fibres can be obtained as follows: one has to take a rational mapping 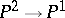 determined by two cubics
determined by two cubics 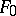 and
and 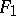 and blow up their 9 points of intersection; or 2)
and blow up their 9 points of intersection; or 2) 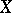 is a surface with
is a surface with 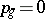 ,
, 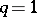 ,
, 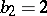 , and the multiplicities
, and the multiplicities 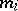 are subject to the inequality
are subject to the inequality
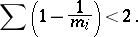 |
The formula for the canonical class and the classification of elliptic surfaces can also be generalized to the case of a field of finite characteristic [5], [6].
The classification of non-algebraic elliptic surfaces.
The classification of non-algebraic elliptic surfaces. For non-algebraic surfaces the algebraic dimension 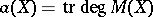 is 1 or 0. If
is 1 or 0. If 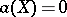 , then
, then 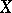 is non-elliptic. All surfaces with
is non-elliptic. All surfaces with 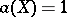 are elliptic. Here the structure of
are elliptic. Here the structure of 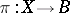 is determined almost canonically: Every such fibration
is determined almost canonically: Every such fibration 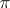 is necessarily elliptic. The classification by the canonical dimension is precisely the same as for algebraic elliptic surfaces:
is necessarily elliptic. The classification by the canonical dimension is precisely the same as for algebraic elliptic surfaces: 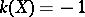
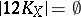 ;
; 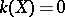
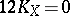 ; and
; and  (
(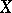 is of basic type)
is of basic type) 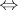
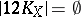 ,
, 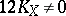 .
.
Non-algebraic elliptic surfaces with 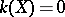 belong to one of the following classes: 1) the
belong to one of the following classes: 1) the 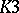 -surfaces (
-surfaces (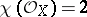 ,
, 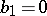 ,
, 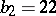 ,
, 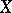 is simply connected); 2) the complex tori (
is simply connected); 2) the complex tori (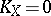 ,
, 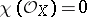 ,
, 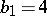 ,
, 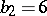 ); 3) the Kodaira surfaces (
); 3) the Kodaira surfaces (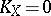 ,
, 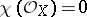 ,
, 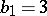 ,
, 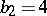 ). Primary Kodaira surfaces are holomorphically locally trivial fibrations over an elliptic curve with an elliptic curve as typical fibre, and from the point of view of differentiability, bundles over a
). Primary Kodaira surfaces are holomorphically locally trivial fibrations over an elliptic curve with an elliptic curve as typical fibre, and from the point of view of differentiability, bundles over a  -dimensional torus with a circle as fibre; or 4) the surfaces with
-dimensional torus with a circle as fibre; or 4) the surfaces with 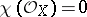 ,
, 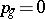 ,
, 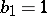 ,
, 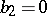 . For them
. For them 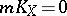 with
with 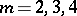 , (analogous to hyper-elliptic surfaces). They have Kodaira surfaces as finite unramified coverings. In the cases 2), 3) and 4)
, (analogous to hyper-elliptic surfaces). They have Kodaira surfaces as finite unramified coverings. In the cases 2), 3) and 4) 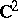 is the universal covering of
is the universal covering of 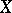 .
.
Non-algebraic elliptic surfaces with 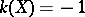 are Hopf surfaces, that is, their universal covering is
are Hopf surfaces, that is, their universal covering is 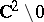 . For them
. For them 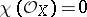 ,
, 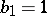 ,
,  . The proper Hopf surfaces are
. The proper Hopf surfaces are 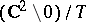 , where
, where 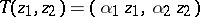 are real generators of
are real generators of 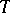 . They are homeomorphic to
. They are homeomorphic to 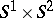 and are characterized by this property. Arbitrary elliptic Hopf surfaces are quotients of proper Hopf surfaces .
and are characterized by this property. Arbitrary elliptic Hopf surfaces are quotients of proper Hopf surfaces .
References
| [1] | "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) |
| [2] | D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1982) pp. 329–420 |
| [3a] | K. Kodaira, "On compact complex analytic surfaces I" Ann. of Math. (2) , 71 (10) pp. 111–152 |
| [3b] | K. Kodaira, "On compact complex analytic surfaces II" Ann. of Math. (2) , 77 (1963) pp. 563–626 |
| [3c] | K. Kodaira, "On compact complex analytic surfaces III" Ann. of Math. (2) , 78 (1963) pp. 1–40 |
| [4a] | K. Kodaira, "On the structure of compact complex analytic surfaces I" Amer. J. Math. , 86 (1964) pp. 751–798 |
| [4b] | K. Kodaira, "On the structure of compact complex analytic surfaces II" Amer. J. Math. , 88 (1966) pp. 682–721 |
| [4c] | K. Kodaira, "On the structure of compact complex analytic surfaces III" Amer. J. Math. , 90 (1968) pp. 55–83 |
| [4d] | K. Kodaira, "On the structure of compact complex analytic surfaces IV" Amer. J. Math. , 90 (1968) pp. 1048–1066 |
| [5] | D. Mumford, "Enriques' classification of surfaces in char 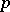 . I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Princeton Univ. Press (1969) pp. 325–339 . I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Princeton Univ. Press (1969) pp. 325–339 |
| [6] | E. Bombieri, D. Mumford, "Enriques' classification of surfaces in char 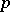 . II" W.L. Baily jr. (ed.) T. Shioda (ed.) , Complex Analysis and Algebraic geometry , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 . II" W.L. Baily jr. (ed.) T. Shioda (ed.) , Complex Analysis and Algebraic geometry , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 |
Comments
A secondary Kodaira surface is a surface other than a primary one, admitting a primary Kodaira surface as an unramified covering. They are elliptic fibrations over a rational curve. Their first Betti number is 1.
The canonical dimension 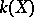 mentioned at the start of the section on classification of algebraic elliptic surfaces is the Kodaira dimension
mentioned at the start of the section on classification of algebraic elliptic surfaces is the Kodaira dimension 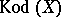 (with
(with  if
if 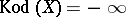 ).
).
References
| [a1] | W. Barth, C. Peters, A. van der Ven, "Compact complex surfaces" , Springer (1984) |
Elliptic surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_surface&oldid=17304