Difference between revisions of "Efficiency, asymptotic"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | e0350701.png | ||
| + | $#A+1 = 42 n = 1 | ||
| + | $#C+1 = 42 : ~/encyclopedia/old_files/data/E035/E.0305070 Efficiency, asymptotic, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''of a test'' | ''of a test'' | ||
A concept that makes it possible in the case of large samples to make a quantitative comparison of two distinct statistical tests for a certain statistical hypothesis. The need to measure the efficiency of tests arose in the 1930s and -forties when simple (from the computational point of view) but "inefficient" rank procedures made their appearance. | A concept that makes it possible in the case of large samples to make a quantitative comparison of two distinct statistical tests for a certain statistical hypothesis. The need to measure the efficiency of tests arose in the 1930s and -forties when simple (from the computational point of view) but "inefficient" rank procedures made their appearance. | ||
| − | There are several distinct approaches to the definition of the asymptotic efficiency of a test. Suppose that a distribution of observations is defined by a real parameter | + | There are several distinct approaches to the definition of the asymptotic efficiency of a test. Suppose that a distribution of observations is defined by a real parameter $ \theta $ |
| + | and that it is required to verify the hypothesis $ H _ {0} $: | ||
| + | $ \theta = \theta _ {0} $ | ||
| + | against the alternative $ H _ {1} $: | ||
| + | $ \theta \neq \theta _ {0} $. | ||
| + | Suppose also that for a certain test with significance level $ \alpha $ | ||
| + | there are $ N _ {1} $ | ||
| + | observations needed to achieve a power $ \beta $ | ||
| + | against the given alternative $ \theta $ | ||
| + | and that another test of the same level needs for this purpose $ N _ {2} $ | ||
| + | observations. Then one can define the relative efficiency of the first test with respect to the second by the formula $ e _ {12} = N _ {2} / N _ {1} $. | ||
| + | The concept of relative efficiency gives exhaustive information for the comparison of tests, but proves to be inconvenient for applications, since $ e _ {12} $ | ||
| + | is a function of the three arguments $ \alpha $, | ||
| + | $ \beta $ | ||
| + | and $ \theta $ | ||
| + | and, as a rule, does not lend itself to computation in explicit form. To overcome this difficulty one uses a passage to a limit. | ||
| − | The quantity | + | The quantity $ \lim\limits _ {\theta \rightarrow \theta _ {0} } e _ {12} ( \alpha , \beta , \theta ) $, |
| + | for fixed $ \alpha $ | ||
| + | and $ \beta $( | ||
| + | if the limit exists), is called the asymptotic relative efficiency in the sense of Pitman. Similarly one defines the asymptotic relative efficiency in the sense of Bahadur, where for fixed $ \beta $, | ||
| + | $ \theta $ | ||
| + | the limit is taken as $ \alpha $ | ||
| + | tends to zero, and the asymptotic relative efficiency in the sense of Hodges and Lehmann, when for fixed $ \alpha $ | ||
| + | and $ \theta $ | ||
| + | one computes the limit as $ \beta \rightarrow 1 $. | ||
Each of these definitions has its own merits and shortfalls. For example, the Pitman efficiency is, as a rule, easier to calculate than the Bahadur one (the calculation of the latter involves the non-trivial problem of studying the asymptotic probability of large deviations of test statistics); however, in a number of cases it turns out to be a less sensitive tool for the comparison of two tests. | Each of these definitions has its own merits and shortfalls. For example, the Pitman efficiency is, as a rule, easier to calculate than the Bahadur one (the calculation of the latter involves the non-trivial problem of studying the asymptotic probability of large deviations of test statistics); however, in a number of cases it turns out to be a less sensitive tool for the comparison of two tests. | ||
| − | Suppose, for example, that the observations are distributed according to the normal law with average | + | Suppose, for example, that the observations are distributed according to the normal law with average $ \theta $ |
| + | and variance 1 and that the hypothesis $ H _ {0} $: | ||
| + | $ \theta = 0 $ | ||
| + | is to be verified against the alternative $ H _ {1} $: | ||
| + | $ \theta > 0 $. | ||
| + | Suppose also that one considers a significance test based on a sample mean $ \overline{X}\; $ | ||
| + | and Student ratio $ t $. | ||
| + | Since the $ t $- | ||
| + | test does not use information on the variance, the optimal test must be that based on $ \overline{X}\; $. | ||
| + | However, from the point of view of Pitman efficiency these tests are equivalent. On the other hand, the Bahadur efficiency of the $ t $- | ||
| + | test in relation to $ \overline{X}\; $ | ||
| + | is strictly less than 1 for any $ \theta > 0 $. | ||
| − | In more complicated cases the Pitman efficiency may depend on | + | In more complicated cases the Pitman efficiency may depend on $ \alpha $ |
| + | or $ \beta $ | ||
| + | and its calculation becomes very tedious. Then one calculates its limiting value as $ \beta \rightarrow 1 $ | ||
| + | or $ \alpha \rightarrow 0 $. | ||
| + | The latter usually is the same as the limiting value of the Bahadur efficiency as $ \theta \rightarrow \theta _ {0} $[[#References|[8]]]. | ||
| − | For other approaches to the definition of asymptotic efficiency of a test see [[#References|[2]]]–[[#References|[5]]]; sequential analogues of this concept are introduced in [[#References|[6]]]–[[#References|[7]]]. The choice of one definition or another must be based on which of them gives a more accurate approximation to the relative efficiency | + | For other approaches to the definition of asymptotic efficiency of a test see [[#References|[2]]]–[[#References|[5]]]; sequential analogues of this concept are introduced in [[#References|[6]]]–[[#References|[7]]]. The choice of one definition or another must be based on which of them gives a more accurate approximation to the relative efficiency $ e _ {12} $; |
| + | however, at present (1988) little is known in this direction [[#References|[9]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Stewart, "The advanced theory of statistics" , '''2. Inference and relationship''' , Griffin (1973)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Bahadur, "Rates of convergence of estimates and test statistics" ''Ann. Math. Stat.'' , '''38''' : 2 (1967) pp. 303–324</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Hodges, E. Lehmann, "The efficiency of some nonparametric competitors of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035070/e03507043.png" />-test" ''Ann. Math. Stat.'' , '''27''' : 2 (1956) pp. 324–335</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Kallenberg, "Chernoff efficiency and deficiency" ''Ann. Statist.'' , '''10''' : 2 (1982) pp. 583–594</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R. Berk, L. Brown, "Sequential Bahadur efficiency" ''Ann. Statist.'' , '''6''' : 3 (1978) pp. 567–581</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R. Berk, "Asymptotic efficiencies of sequential tests" ''Ann. Statist.'' , '''4''' : 5 (1976) pp. 891–911</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> H. Wieland, "A condition under which the Pitman and Bahadur approaches to efficiency coincide" ''Ann. Statist.'' , '''4''' : 5 (1976) pp. 1003–1011</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> P. Groeneboom, J. Oosterhoff, "Bahadur efficiency and small-sample efficiency" ''Internat. Stat. Rev.'' , '''49''' : 2 (1981) pp. 127–141</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Stewart, "The advanced theory of statistics" , '''2. Inference and relationship''' , Griffin (1973)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Bahadur, "Rates of convergence of estimates and test statistics" ''Ann. Math. Stat.'' , '''38''' : 2 (1967) pp. 303–324</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Hodges, E. Lehmann, "The efficiency of some nonparametric competitors of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035070/e03507043.png" />-test" ''Ann. Math. Stat.'' , '''27''' : 2 (1956) pp. 324–335</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Kallenberg, "Chernoff efficiency and deficiency" ''Ann. Statist.'' , '''10''' : 2 (1982) pp. 583–594</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R. Berk, L. Brown, "Sequential Bahadur efficiency" ''Ann. Statist.'' , '''6''' : 3 (1978) pp. 567–581</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R. Berk, "Asymptotic efficiencies of sequential tests" ''Ann. Statist.'' , '''4''' : 5 (1976) pp. 891–911</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> H. Wieland, "A condition under which the Pitman and Bahadur approaches to efficiency coincide" ''Ann. Statist.'' , '''4''' : 5 (1976) pp. 1003–1011</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> P. Groeneboom, J. Oosterhoff, "Bahadur efficiency and small-sample efficiency" ''Internat. Stat. Rev.'' , '''49''' : 2 (1981) pp. 127–141</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 19:36, 5 June 2020
of a test
A concept that makes it possible in the case of large samples to make a quantitative comparison of two distinct statistical tests for a certain statistical hypothesis. The need to measure the efficiency of tests arose in the 1930s and -forties when simple (from the computational point of view) but "inefficient" rank procedures made their appearance.
There are several distinct approaches to the definition of the asymptotic efficiency of a test. Suppose that a distribution of observations is defined by a real parameter $ \theta $ and that it is required to verify the hypothesis $ H _ {0} $: $ \theta = \theta _ {0} $ against the alternative $ H _ {1} $: $ \theta \neq \theta _ {0} $. Suppose also that for a certain test with significance level $ \alpha $ there are $ N _ {1} $ observations needed to achieve a power $ \beta $ against the given alternative $ \theta $ and that another test of the same level needs for this purpose $ N _ {2} $ observations. Then one can define the relative efficiency of the first test with respect to the second by the formula $ e _ {12} = N _ {2} / N _ {1} $. The concept of relative efficiency gives exhaustive information for the comparison of tests, but proves to be inconvenient for applications, since $ e _ {12} $ is a function of the three arguments $ \alpha $, $ \beta $ and $ \theta $ and, as a rule, does not lend itself to computation in explicit form. To overcome this difficulty one uses a passage to a limit.
The quantity $ \lim\limits _ {\theta \rightarrow \theta _ {0} } e _ {12} ( \alpha , \beta , \theta ) $, for fixed $ \alpha $ and $ \beta $( if the limit exists), is called the asymptotic relative efficiency in the sense of Pitman. Similarly one defines the asymptotic relative efficiency in the sense of Bahadur, where for fixed $ \beta $, $ \theta $ the limit is taken as $ \alpha $ tends to zero, and the asymptotic relative efficiency in the sense of Hodges and Lehmann, when for fixed $ \alpha $ and $ \theta $ one computes the limit as $ \beta \rightarrow 1 $.
Each of these definitions has its own merits and shortfalls. For example, the Pitman efficiency is, as a rule, easier to calculate than the Bahadur one (the calculation of the latter involves the non-trivial problem of studying the asymptotic probability of large deviations of test statistics); however, in a number of cases it turns out to be a less sensitive tool for the comparison of two tests.
Suppose, for example, that the observations are distributed according to the normal law with average $ \theta $ and variance 1 and that the hypothesis $ H _ {0} $: $ \theta = 0 $ is to be verified against the alternative $ H _ {1} $: $ \theta > 0 $. Suppose also that one considers a significance test based on a sample mean $ \overline{X}\; $ and Student ratio $ t $. Since the $ t $- test does not use information on the variance, the optimal test must be that based on $ \overline{X}\; $. However, from the point of view of Pitman efficiency these tests are equivalent. On the other hand, the Bahadur efficiency of the $ t $- test in relation to $ \overline{X}\; $ is strictly less than 1 for any $ \theta > 0 $.
In more complicated cases the Pitman efficiency may depend on $ \alpha $ or $ \beta $ and its calculation becomes very tedious. Then one calculates its limiting value as $ \beta \rightarrow 1 $ or $ \alpha \rightarrow 0 $. The latter usually is the same as the limiting value of the Bahadur efficiency as $ \theta \rightarrow \theta _ {0} $[8].
For other approaches to the definition of asymptotic efficiency of a test see [2]–[5]; sequential analogues of this concept are introduced in [6]–[7]. The choice of one definition or another must be based on which of them gives a more accurate approximation to the relative efficiency $ e _ {12} $; however, at present (1988) little is known in this direction [9].
References
| [1] | A. Stewart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1973) |
| [2] | R. Bahadur, "Rates of convergence of estimates and test statistics" Ann. Math. Stat. , 38 : 2 (1967) pp. 303–324 |
| [3] | J. Hodges, E. Lehmann, "The efficiency of some nonparametric competitors of the 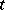 -test" Ann. Math. Stat. , 27 : 2 (1956) pp. 324–335 -test" Ann. Math. Stat. , 27 : 2 (1956) pp. 324–335 |
| [4] | C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965) |
| [5] | W. Kallenberg, "Chernoff efficiency and deficiency" Ann. Statist. , 10 : 2 (1982) pp. 583–594 |
| [6] | R. Berk, L. Brown, "Sequential Bahadur efficiency" Ann. Statist. , 6 : 3 (1978) pp. 567–581 |
| [7] | R. Berk, "Asymptotic efficiencies of sequential tests" Ann. Statist. , 4 : 5 (1976) pp. 891–911 |
| [8] | H. Wieland, "A condition under which the Pitman and Bahadur approaches to efficiency coincide" Ann. Statist. , 4 : 5 (1976) pp. 1003–1011 |
| [9] | P. Groeneboom, J. Oosterhoff, "Bahadur efficiency and small-sample efficiency" Internat. Stat. Rev. , 49 : 2 (1981) pp. 127–141 |
Comments
Reference [a1] (and other work) suggest that, in the practically important case of small sample situations, the Pitman approach yields, in general, better approximations than the Bahadur approach does.
References
| [a1] | P. Groeneboom, J. Oosterhoff, "Bahadur efficiencies and probabilities of large deviations" Stat. Neerlandica , 31 (1977) pp. 1–24 |
Efficiency, asymptotic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Efficiency,_asymptotic&oldid=46791