Domination
An order relation for differential operators formulated in terms of the characteristic polynomial 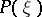 . For example, if
. For example, if
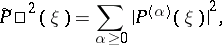 |
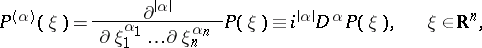 |
then 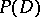 is stronger than
is stronger than 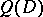 if for any
if for any 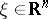 ,
,
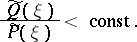 |
There also exist other definitions of domination; see [1].
References
| [1] | L. Hörmander, "Linear partial differential operators" , Springer (1963) |
Comments
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 2 , Springer (1983) pp. §10.4 |
Domination in the theory of games is a relation expressing the superiority of one object (strategy (in game theory); sharing) over another. Domination of strategies: A strategy  of player
of player 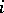 dominates (strictly dominates) his strategy
dominates (strictly dominates) his strategy 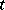 if his pay-off in any situation containing
if his pay-off in any situation containing  is not smaller (is greater) than his pay-off in the situation comprising the same strategies of the other players and the strategy
is not smaller (is greater) than his pay-off in the situation comprising the same strategies of the other players and the strategy 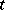 . Domination of sharings (in a cooperative game): A sharing
. Domination of sharings (in a cooperative game): A sharing  dominates a sharing
dominates a sharing 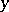 (denoted by
(denoted by 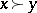 ) if there exists a non-empty coalition
) if there exists a non-empty coalition 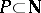 such that
such that
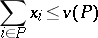 |
and 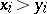 for
for 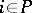 (where
(where  is the characteristic function of the game).
is the characteristic function of the game).
I.N. Vrublevskaya
Comments
Instead of sharing the terms imputation and pay-off vector are also used (see also Gain function).
References
| [a1] | G. Owen, "Game theory" , Acad. Press (1982) |
Domination in potential theory is an order relation 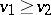 between functions, in particular between potentials of specific classes, i.e. a fulfillment of the inequality
between functions, in particular between potentials of specific classes, i.e. a fulfillment of the inequality  for all
for all  in the common domain of definition of
in the common domain of definition of 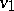 and
and 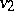 . In various domination principles the relation
. In various domination principles the relation 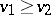 is established as the result of the inequality
is established as the result of the inequality 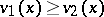 on some proper subsets in the domains of definition. The simplest Cartan domination principle is: Let
on some proper subsets in the domains of definition. The simplest Cartan domination principle is: Let  be a non-negative superharmonic function (cf. Subharmonic function) on the Euclidean space
be a non-negative superharmonic function (cf. Subharmonic function) on the Euclidean space  ,
, 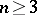 , and let
, and let 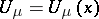 be the Newton potential of a measure
be the Newton potential of a measure  of finite energy (cf. Energy of measures). Then, if
of finite energy (cf. Energy of measures). Then, if 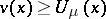 on some set
on some set  such that
such that 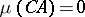 , the domination
, the domination  holds. See also Potential theory, abstract.
holds. See also Potential theory, abstract.
References
| [1] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
| [2] | M. Brelot, "On topologies and boundaries in potential theory" , Springer (1971) |
E.D. Solomentsev
Comments
There are some more concepts in mathematics which involve the word dominant or domination. Thus, a sequence of constants  for a sequence of functions
for a sequence of functions 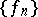 such that
such that 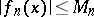 for all
for all  is called a dominant or majorant of
is called a dominant or majorant of 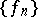 .
.
In algebraic geometry one speaks of a dominant morphism 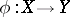 if
if 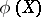 is dense in
is dense in 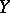 .
.
In the theory of commutative local rings, if 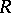 ,
, 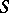 are both local rings contained in a field
are both local rings contained in a field 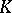 , then
, then  dominates
dominates 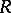 if
if 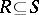 but
but 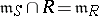 , where
, where  is the maximal ideal of
is the maximal ideal of 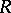 .
.
Finally, cf. Representation of a Lie algebra and Representation with a highest weight vector for the notions of a dominant weight and a dominant linear form.
The Cartan domination principle is also called Cartan's maximum principle. Let  be a real-valued function on
be a real-valued function on 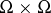 ,
, 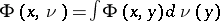 for a measure
for a measure  on
on  . The kernel
. The kernel  is said to satisfy the balayage principle, or sweeping-out principle, if for each compact set
is said to satisfy the balayage principle, or sweeping-out principle, if for each compact set 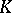 and measure
and measure 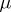 supported by
supported by 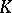 there is a measure
there is a measure  supported by
supported by 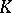 such that
such that 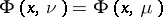 quasi-everywhere on
quasi-everywhere on 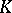 and
and 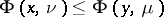 in
in  . The measure
. The measure  is the balayage of
is the balayage of 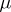 ; cf. also Balayage method. Let
; cf. also Balayage method. Let 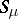 be the support of
be the support of 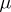 . Then the balayage principle implies the Cartan domination principle in the form that if
. Then the balayage principle implies the Cartan domination principle in the form that if 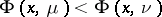 on
on 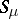 for some
for some 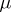 of finite energy and some
of finite energy and some  , then the same holds in
, then the same holds in  . (The measure
. (The measure 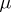 has finite energy if
has finite energy if 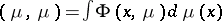 is finite.) The potential is said to satisfy the inverse domination principle if
is finite.) The potential is said to satisfy the inverse domination principle if 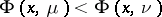 on
on 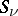 for
for 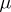 of finite energy and any
of finite energy and any  implies the same inequality in
implies the same inequality in  .
.
In abstract potential theory the Cartan domination principle simplifies to the "axiom of dominationaxiom of domination" . Let 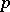 be a locally bounded potential, harmonic on the open set
be a locally bounded potential, harmonic on the open set 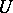 , and let
, and let  be a positive hyperharmonic function (cf. Poly-harmonic function). If
be a positive hyperharmonic function (cf. Poly-harmonic function). If 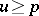 on the complement of
on the complement of 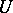 , then
, then 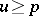 . See [a1] for a survey of related properties.
. See [a1] for a survey of related properties.
References
| [a1] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
| [a2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 |
Domination. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Domination&oldid=16235