Difference between revisions of "Diophantine equations"
m (→Comments: fix) |
m (link) |
||
| Line 23: | Line 23: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032610/d03261014.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032610/d03261014.png" /></td> </tr></table> | ||
| − | Positive integral solutions of this equation represent the lengths of the small sides <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032610/d03261015.png" /> and of the hypotenuse <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032610/d03261016.png" /> of right-angled triangles with integral side lengths; these numbers are known as Pythagorean numbers. All triplets of relatively prime Pythagorean numbers are given by the formulas | + | Positive integral solutions of this equation represent the lengths of the small sides <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032610/d03261015.png" /> and of the hypotenuse <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032610/d03261016.png" /> of right-angled triangles with integral side lengths; these numbers are known as [[Pythagorean numbers]]. All triplets of relatively prime Pythagorean numbers are given by the formulas |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032610/d03261017.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032610/d03261017.png" /></td> </tr></table> | ||
Revision as of 07:31, 10 December 2016
Algebraic equations, or systems of algebraic equations with rational coefficients, the solutions of which are sought for in integers or rational numbers. It is usually assumed that the number of unknowns in Diophantine equations is larger than the number of equations; thus, they are also known as indefinite equations. In modern mathematics the concept of a Diophantine equation is also applied to algebraic equations the solutions of which are sought for in the algebraic integers of some algebraic extension of the field 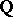 of rational numbers, of the field of
of rational numbers, of the field of 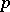 -adic numbers, etc.
-adic numbers, etc.
The study of Diophantine equations is on the border-line between number theory and algebraic geometry (cf. Diophantine geometry).
Finding solutions of equations in integers is one of the oldest mathematical problems. As early as the beginning of the second millennium B.C. ancient Babylonians succeeded in solving systems of equations with two unknowns. This branch of mathematics flourished to the greatest extent in Ancient Greece. The principal source is Aritmetika by Diophantus (probably the 3rd century A.D.), which contains different types of equations and systems. In this book, Diophantus (hence the name "Diophantine equations" ) anticipated a number of methods for the study of equations of the second and third degrees which were only fully developed in the 19th century [1]. The creation of the theory of rational numbers by the scientists of Ancient Greece led to the study of rational solutions of indefinite equations. This point of view is systematically followed by Diophantus in his book. Even though his work contains solutions of specific Diophantine equations only, there is reason to believe that he was also familiar with a few general methods.
The study of Diophantine equations usually involves major difficulties. Moreover, it is possible to specify, explicitly, polynomials
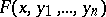 |
with integer coefficients such that no algorithm exists by which it would be possible to tell, for any given  , whether the equation
, whether the equation
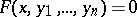 |
is solvable for  (cf. Diophantine equations, solvability problem of). Examples of such polynomials may be explicitly written down; no exhaustive description of their solutions can be given (if the Church thesis is accepted).
(cf. Diophantine equations, solvability problem of). Examples of such polynomials may be explicitly written down; no exhaustive description of their solutions can be given (if the Church thesis is accepted).
The simplest Diophantine equation
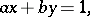 |
where  and
and 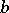 are relatively prime integers, has infinitely many solutions (if
are relatively prime integers, has infinitely many solutions (if 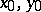 form a solution, then the pair of numbers
form a solution, then the pair of numbers 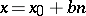 and
and 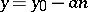 , where
, where  is an arbitrary integer, will also be a solution). Another example of a Diophantine equation is
is an arbitrary integer, will also be a solution). Another example of a Diophantine equation is
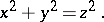 |
Positive integral solutions of this equation represent the lengths of the small sides 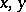 and of the hypotenuse
and of the hypotenuse  of right-angled triangles with integral side lengths; these numbers are known as Pythagorean numbers. All triplets of relatively prime Pythagorean numbers are given by the formulas
of right-angled triangles with integral side lengths; these numbers are known as Pythagorean numbers. All triplets of relatively prime Pythagorean numbers are given by the formulas
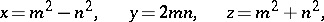 |
where 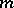 and
and  are relatively prime integers (
are relatively prime integers (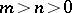 ).
).
Diophantus in his Aritmetika deals with the search for rational (not necessarily integral) solutions of special types of Diophantine equations. The general theory of solving of Diophantine equations of the first degree was developed by C.G. Bachet in the 17th century; for more details on this subject see Linear equation. P. Fermat, J. Wallis, L. Euler, J.L. Lagrange, and C.F. Gauss in the early 19th century mainly studied Diophantine equations of the form
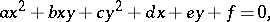 |
where  ,
, 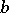 ,
,  ,
, 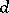 ,
,  , and
, and 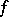 are integers, i.e. general inhomogeneous equations of the second degree with two unknowns. Lagrange used continued fractions in his study of general inhomogeneous Diophantine equations of the second degree with two unknowns. Gauss developed the general theory of quadratic forms, which is the basis of solving certain types of Diophantine equations.
are integers, i.e. general inhomogeneous equations of the second degree with two unknowns. Lagrange used continued fractions in his study of general inhomogeneous Diophantine equations of the second degree with two unknowns. Gauss developed the general theory of quadratic forms, which is the basis of solving certain types of Diophantine equations.
In studies on Diophantine equations of degrees higher than two significant success was attained only in the 20th century. It was established by A. Thue that the Diophantine equation
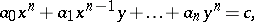 |
where 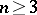 ,
, 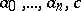 are integers, and the polynomial
are integers, and the polynomial 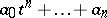 is irreducible in the field of rational numbers, cannot have an infinite number of integer solutions. However, Thue's method fails to yield either a bound on the solutions or on their number. A. Baker obtained effective theorems giving bounds on solutions of certain equations of this kind. B.N. Delone proposed another method of investigation, which is applicable to a narrower class of Diophantine equations, but which yields a bound for the number of solutions. In particular, Diophantine equations of the form
is irreducible in the field of rational numbers, cannot have an infinite number of integer solutions. However, Thue's method fails to yield either a bound on the solutions or on their number. A. Baker obtained effective theorems giving bounds on solutions of certain equations of this kind. B.N. Delone proposed another method of investigation, which is applicable to a narrower class of Diophantine equations, but which yields a bound for the number of solutions. In particular, Diophantine equations of the form
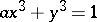 |
are fully solvable by this method.
The theory of Diophantine equations has many directions. Thus, a well-known problem in this theory is Fermat's problem — the hypothesis according to which there are no non-trivial solutions of the Diophantine equation
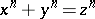 | (1) |
if 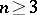 . The study of integer solutions of equation (1) is a natural generalization of the problem of Pythagorean triplets. Euler obtained a positive solution of Fermat's problem for
. The study of integer solutions of equation (1) is a natural generalization of the problem of Pythagorean triplets. Euler obtained a positive solution of Fermat's problem for 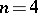 . Owing to this result, Fermat's problem is reduced to the proof of the absence of non-zero integer solutions of equation (1) if
. Owing to this result, Fermat's problem is reduced to the proof of the absence of non-zero integer solutions of equation (1) if  is an odd prime. At the time of writing (1988) the study concerned with solving (1) has not been completed. The difficulties involved in solving it are due to the fact that prime factorization in the ring of algebraic integers is not unique. The theory of divisors in rings of algebraic integers makes it possible to confirm the validity of Fermat's theorem for many classes of prime exponents
is an odd prime. At the time of writing (1988) the study concerned with solving (1) has not been completed. The difficulties involved in solving it are due to the fact that prime factorization in the ring of algebraic integers is not unique. The theory of divisors in rings of algebraic integers makes it possible to confirm the validity of Fermat's theorem for many classes of prime exponents  .
.
The arithmetic of rings of algebraic integers is also utilized in many other problems in Diophantine equations. For instance, such methods were applied in a detailed solution of an equation of the form
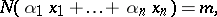 | (2) |
where 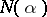 is the norm of the algebraic number
is the norm of the algebraic number 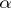 , and integral rational numbers
, and integral rational numbers  which satisfy equation (2) are to be found. Equations of this class include, in particular, the Pell equation
which satisfy equation (2) are to be found. Equations of this class include, in particular, the Pell equation 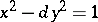 . Depending on the values of
. Depending on the values of  which appear in (2), these equations are subdivided into two types. The first type — the so-called complete forms — comprises equations in which among the
which appear in (2), these equations are subdivided into two types. The first type — the so-called complete forms — comprises equations in which among the 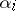 there are
there are 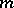 linearly independent numbers over the field of rational numbers
linearly independent numbers over the field of rational numbers 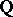 , where
, where 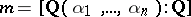 is the degree of the algebraic number field
is the degree of the algebraic number field 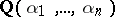 over
over  . Incomplete forms are those in which the maximum number of linearly independent numbers
. Incomplete forms are those in which the maximum number of linearly independent numbers 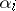 is less than
is less than 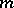 . The case of complete forms is simpler and its study has now, in principle, been completed. It is possible, for example, to describe all solutions of any complete form [2].
. The case of complete forms is simpler and its study has now, in principle, been completed. It is possible, for example, to describe all solutions of any complete form [2].
The second type — the incomplete forms — is more complicated, and the development of its theory is still (1988) far from being completed. Such equations are studied with the aid of Diophantine approximations. They include the equation
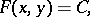 |
where 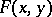 is an irreducible homogeneous polynomial of degree
is an irreducible homogeneous polynomial of degree 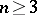 . This equation may be written as
. This equation may be written as
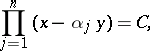 | (3) |
where 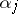 are all the roots of the polynomial
are all the roots of the polynomial  . The existence of an infinite sequence of integral solutions of equation (3) would lead to relationships of the form
. The existence of an infinite sequence of integral solutions of equation (3) would lead to relationships of the form
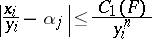 | (4) |
for some 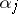 . Without loss of generality, one may assume that
. Without loss of generality, one may assume that 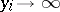 . Accordingly, if
. Accordingly, if 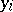 is sufficiently large, inequality (4) will be in contradiction with the Thue–Siegel–Roth theorem, from which follows that the equation
is sufficiently large, inequality (4) will be in contradiction with the Thue–Siegel–Roth theorem, from which follows that the equation 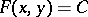 , where
, where 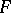 is an irreducible form of degree three or higher, cannot have an infinite number of solutions.
is an irreducible form of degree three or higher, cannot have an infinite number of solutions.
Equations such as (2) constitute a fairly narrow class among all Diophantine equations. For instance, their simple appearance notwithstanding, the equations
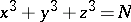 | (5) |
and
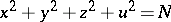 | (6) |
are not in this class. The study of the solutions of equation (6) is a fairly thoroughly investigated branch of Diophantine equations — the representation of numbers by quadratic forms. The Lagrange theorem states that (6) is solvable for all natural  . Any natural number not representable in the form
. Any natural number not representable in the form 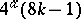 , where
, where  and
and 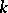 are non-negative integers, can be represented as a sum of three squares (Gauss' theorem). Criteria are known for the existence of rational or integral solutions of equations of the form
are non-negative integers, can be represented as a sum of three squares (Gauss' theorem). Criteria are known for the existence of rational or integral solutions of equations of the form
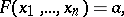 |
where 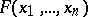 is a quadratic form with integer coefficients. Thus, according to Minkowski–Hasse theorem, the equation
is a quadratic form with integer coefficients. Thus, according to Minkowski–Hasse theorem, the equation
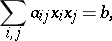 |
where  and
and 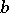 are rational, has a rational solution if and only if it is solvable in real numbers and in
are rational, has a rational solution if and only if it is solvable in real numbers and in 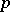 -adic numbers for each prime number
-adic numbers for each prime number 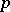 .
.
The representation of numbers by arbitrary forms of the third degree or higher has been studied to a lesser extent, because of inherent difficulties. One of the principal methods of study in the representation of numbers by forms of higher degree is the method of trigonometric sums (cf. Trigonometric sums, method of). In this method the number of solutions of the equation is explicitly written out in terms of a Fourier integral, after which the circle method is employed to express the number of solutions of the equation in terms of the number of solutions of the corresponding congruences. The method of trigonometric sums depends less than do other methods on the algebraic peculiarities of the equation.
There exists a large number of specific Diophantine equations which are solvable by elementary methods [5].
References
| [1] | I.M. Vinogradov, "Fundamentals of number theory" , Moscow (1972) (In Russian) |
| [2] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) MR0195803 Zbl 0145.04902 |
| [3] | L.E. Dickson, "History of the theory of numbers" , 1 , Chelsea, reprint (1934) MR1793101 MR1720467 MR0245501 MR0245500 MR0245499 MR1520248 MR1519706 MR1519382 Zbl 60.0817.03 |
| [4] | I.G. Bashmakov, "Diophant und diophantische Gleichungen" , Deutsch. Verlag Wissenschaft. (1974) (Translated from Russian) |
| [5] | W. Sierpiński, "On solution of equations in integers" , PWN (1956) (In Polish) |
Comments
The most outstanding recent result in the study of Diophantine equations was the proof by G. Falting of the Mordell conjecture, stating that curves of genus 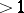 (cf. Genus of a curve) over algebraic fields have no more than a finite number of rational points (cf. [a1]). From this result it follows, in particular, that the Fermat equation
(cf. Genus of a curve) over algebraic fields have no more than a finite number of rational points (cf. [a1]). From this result it follows, in particular, that the Fermat equation  has only a finite number of rational solutions for
has only a finite number of rational solutions for 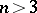 .
.
In the last decade there was also some progress in dealing with cubic forms (cf. Cubic form) and systems of equations consisting of pairs of quadratic forms (cf. Quadratic form). This development was based on cohomological methods that provide an obstruction to the Hasse principle. These methods were suggested by Yu.I. Manin (cf. [a2]) and are now called the Brauer–Manin obstruction to the Hasse principle. It was conjectured in [a3] that the Brauer–Manin obstruction is the only one to the Hasse principle for rational surfaces. This was verified in many cases, for example, for all cubic equations 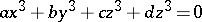 where
where  ,
,  ,
,  ,
, 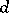 are positive integers less than 100 ([a5]). By application of suitable hyperplane sections the problem of existence of rational solutions for cubic equations with
are positive integers less than 100 ([a5]). By application of suitable hyperplane sections the problem of existence of rational solutions for cubic equations with 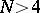 variables, or for a pair of quadratic equations with
variables, or for a pair of quadratic equations with 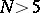 variables, can be reduced to the problem for rational surfaces (cf. Rational surface) for which the existence of rational points (or, equivalently, of rational solutions for a corresponding system of equations) can be effectively verified. In particular, this method gives lower bounds for
variables, can be reduced to the problem for rational surfaces (cf. Rational surface) for which the existence of rational points (or, equivalently, of rational solutions for a corresponding system of equations) can be effectively verified. In particular, this method gives lower bounds for 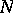 for which the system of two quadratic equations has solutions that are better than those obtained by the present circle method ([a4]).
for which the system of two quadratic equations has solutions that are better than those obtained by the present circle method ([a4]).
Applications of transcendental number theory to Diophantine equations can be found in [a11], [a12]. Diophantine equations from the point of view of algebraic geometry are treated in [a6], [a13]. Monographs dealing specifically with Fermat's equation (cf. also Fermat great theorem) are [a8] and [a14].
References
| [a1] | G. Faltings, "Endlichkeitssätze fur abelsche varietäten über Zahlkörpern" Invent. Math. , 73 (1983) pp. 349–366 MR0718935 MR0732554 Zbl 0588.14026 |
| [a2] | Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1974) (Translated from Russian) MR0460349 Zbl 0277.14014 |
| [a3a] | J.L. Colliot-Thélène, J.J. Sansuc, "La descente sur les varietes rationnelle" A. Beauville (ed.) , Journées de géométrie algébrique d'Angers (1979) , Sijthoff & Noordhoff (1980) pp. 223–227 |
| [a3b] | J.L. Colliot-Thélène, J.J. Sansuc, "La descente sur les varietes rationnelles II" Duke Math. J. , 54 (1987) pp. 375–492 MR899402 Zbl 0659.14028 |
| [a4a] | J.L. Colliot-Thélène, J.J. Sansuc, P. Swinnerton-Dyer, "Intersection of two quadrics and Chatelet surfaces" J. Reine Angew. Math. , 373 (1987) pp. 37–107 |
| [a4b] | J.L. Colliot-Thélène, J.J. Sansuc, P. Swinnerton-Dyer, "Intersection of two quadrics and Chatelet surfaces" J. Reine Angew. Math. , 374 (1987) pp. 72–168 |
| [a5] | J.L. Colliot-Thélène, D. Kanevsky, J.J. Sansuc, "Aritmétique des surfaces cubiques diagonales" , Lect. notes in math. , 1290 , Springer (1987) pp. 1–109 |
| [a6] | S. Lang, "Diophantine geometry" , Interscience (1962) MR0142550 Zbl 0115.38701 |
| [a7] | L.J. Mordell, "Diophantine equations" , Acad. Press (1969) MR0260670 MR0249355 MR0236108 MR0231785 MR0241361 Zbl 0188.34503 Zbl 0186.36001 Zbl 0167.04005 |
| [a8] | H.M. Edwards, "Fermat's last theorem. A genetic introduction to algebraic number theory" , Springer (1977) |
| [a9] | A. Weil, "Number theory: an approach through history: from Hammupari to Legendre" , Birkhäuser (1984) |
| [a10] | B.L. van der Waerden, "Geometry and algebra in ancient civilisations" , Springer (1983) |
| [a11] | A. Baker, "Transcendental number theory" , Cambridge Univ. Press (1975) MR0422171 Zbl 0297.10013 |
| [a12] | T.N. Shorey, R. Tijdeman, "Exponential Diophantine equations" , Cambridge Univ. Press (1987) MR1766003 MR1764814 MR1335008 MR1441334 MR0972011 MR0891406 Zbl 1156.11015 Zbl 0961.11012 Zbl 0958.11026 Zbl 0973.11501 Zbl 0748.11022 Zbl 0658.10024 Zbl 0606.10011 |
| [a13] | S. Lang, "Fundamentals of Diophantine geometry" , Springer (1983) MR0715605 Zbl 0528.14013 |
| [a14] | P. Ribenboim, "Thirteen lectures on Fermat's last theorem" , Springer (1979) |
| [a15] | H. Hasse, "Number theory" , Springer (1980) (Translated from German) MR0544018 MR0562104 Zbl 0423.12002 |
Diophantine equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diophantine_equations&oldid=39946