Differentiation of a mapping
Finding the differential or, in other words, the principal linear part (of increment) of the mapping. The finding of the differential, i.e. the approximation of the mapping in a neighbourhood of some point by linear mappings, is a highly important operation in differential calculus. A very general framework for differential calculus can be formulated in the setting of topological vector spaces.
Let  and
and  be topological vector spaces. Let a mapping
be topological vector spaces. Let a mapping  be defined on an open subset
be defined on an open subset  of
of  and let it take values in
and let it take values in  . If the difference
. If the difference  , where
, where  and
and  , can be approximated by a function
, can be approximated by a function  which is linear with respect to the increment
which is linear with respect to the increment 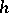 , then
, then 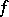 is known as a differentiable mapping at
is known as a differentiable mapping at 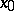 . The approximating linear function
. The approximating linear function 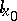 is said to be the derivative or the differential of the mapping at
is said to be the derivative or the differential of the mapping at 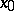 and is denoted by the symbol
and is denoted by the symbol 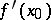 or
or 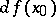 . Mappings with identical derivatives at a given point are said to be mutually tangent mappings at this point. The value of the approximating function on an element
. Mappings with identical derivatives at a given point are said to be mutually tangent mappings at this point. The value of the approximating function on an element 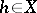 , denoted by the symbol
, denoted by the symbol 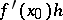 ,
,  or
or 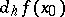 , is known as the differential of the mapping
, is known as the differential of the mapping  at the point
at the point  for the increment
for the increment 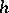 .
.
Depending on the meaning attributed to the approximation of the increment  by a linear expression in
by a linear expression in 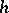 , there result different concepts of differentiability and of the derivative. For the most important existing definitions see [1], .
, there result different concepts of differentiability and of the derivative. For the most important existing definitions see [1], .
Let 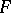 be the set of all mappings from
be the set of all mappings from 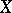 into
into 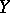 and let
and let  be some topology or pseudo-topology in
be some topology or pseudo-topology in  . A mapping
. A mapping  is small at zero if the curve
is small at zero if the curve
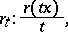 |
conceived of as a mapping
 |
of the straight line  into
into 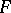 , is continuous at zero in the (pseudo-) topology
, is continuous at zero in the (pseudo-) topology  . Now, a mapping
. Now, a mapping 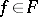 is differentiable at a point
is differentiable at a point 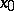 if there exists a continuous linear mapping
if there exists a continuous linear mapping  such that the mapping
such that the mapping
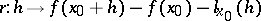 |
is small at zero. Depending on the choice of  in
in 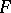 various definitions of derivatives are obtained. Thus, if the topology of pointwise convergence is selected for
various definitions of derivatives are obtained. Thus, if the topology of pointwise convergence is selected for  , one obtains differentiability according to Gâteaux (cf. Gâteaux derivative). If
, one obtains differentiability according to Gâteaux (cf. Gâteaux derivative). If 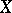 and
and 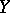 are Banach spaces and the topology in
are Banach spaces and the topology in 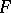 is the topology of uniform convergence on bounded sets in
is the topology of uniform convergence on bounded sets in  , one obtains differentiability according to Fréchet (cf. Fréchet derivative).
, one obtains differentiability according to Fréchet (cf. Fréchet derivative).
If 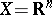 and
and  , the derivative
, the derivative  of a differentiable mapping
of a differentiable mapping 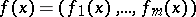 , where
, where  , is defined by the Jacobi matrix
, is defined by the Jacobi matrix  , and is a continuous linear mapping from
, and is a continuous linear mapping from 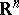 into
into 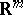 .
.
Derivatives of mappings display many of the properties of the derivatives of functions of one variable. For instance, under very general assumptions, they display the property of linearity:
 |
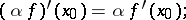 |
and in many cases the formula for differentiation of composite functions:
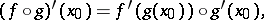 |
is applicable; the generalized mean-value theorem of Lagrange is valid for mappings into locally convex spaces.
The concept of a differentiable mapping is extended to the case when 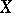 and
and 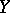 are smooth differentiable manifolds, both finite-dimensional and infinite-dimensional [4], [5], [6]. Differentiable mappings between infinite-dimensional spaces and their derivatives were defined for the first time by V. Volterra (1887), M. Fréchet (1911) and R. Gâteaux (1913). For a more detailed history of the development of the concept of a derivative in higher-dimensional spaces see .
are smooth differentiable manifolds, both finite-dimensional and infinite-dimensional [4], [5], [6]. Differentiable mappings between infinite-dimensional spaces and their derivatives were defined for the first time by V. Volterra (1887), M. Fréchet (1911) and R. Gâteaux (1913). For a more detailed history of the development of the concept of a derivative in higher-dimensional spaces see .
References
| [1] | A. Frölicher, W. Bucher, "Calculus in vector spaces without norm" , Lect. notes in math. , 30 , Springer (1966) |
| [2a] | V.I. Averbukh, O.G. Smolyanov, "The theory of differentiation in linear topological spaces" Russian Math. Surveys , 22 : 6 (1967) pp. 201–258 Uspekhi Mat. Nauk , 22 : 6 (1967) pp. 201–260 |
| [2b] | V.I. Averbukh, O.G. Smolyanov, "The various definitions of the derivative in linear topological spaces" Russian Math. Surveys , 23 : 4 (1968) pp. 67–113 Uspekhi Mat. Nauk , 23 : 4 (1968) pp. 67–116 |
| [3] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1961) (Translated from French) |
| [4] | S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III |
| [5] | N. Bourbaki, "Elements of mathematics. Differentiable and analytic manifolds" , Addison-Wesley (1966) (Translated from French) |
| [6] | M. Spivak, "Calculus on manifolds" , Benjamin (1965) |
Differentiation of a mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differentiation_of_a_mapping&oldid=14853