Descent, method of
A method for solving the minimization problem
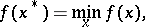 |
where 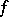 is some function of the variables
is some function of the variables  . The iterative sequence
. The iterative sequence  of the method of descent is computed by the formula
of the method of descent is computed by the formula
 |
where  is a vector indicating some direction of decrease of
is a vector indicating some direction of decrease of 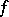 at
at  , and
, and  is an iterative parameter, the value of which indicates the step-length in the direction
is an iterative parameter, the value of which indicates the step-length in the direction 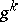 . If
. If 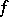 is a differentiable function and
is a differentiable function and 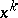 is not an extremal point of it, then the vector
is not an extremal point of it, then the vector 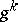 must satisfy the inequality
must satisfy the inequality
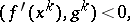 | (*) |
where 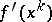 is the gradient of
is the gradient of 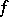 at
at 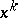 .
.
If 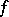 is a sufficiently smooth function (e.g. twice continuously differentiable) and if the sequence
is a sufficiently smooth function (e.g. twice continuously differentiable) and if the sequence 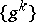 satisfies inequality (*), then there exists a sequence
satisfies inequality (*), then there exists a sequence 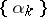 such that
such that
 |
Under certain restrictions (see [3]) on the function 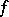 and on the method of choosing the parameters
and on the method of choosing the parameters 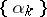 and the vectors
and the vectors 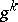 , the sequence
, the sequence  converges to a solution
converges to a solution 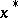 of the initial problem.
of the initial problem.
The gradient method, in which the vectors 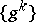 are in some way expressed in terms of the vectors
are in some way expressed in terms of the vectors 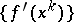 , is a method of descent. One of the most common cases is when
, is a method of descent. One of the most common cases is when
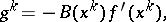 |
where  is a symmetric matrix satisfying
is a symmetric matrix satisfying
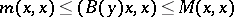 |
for any two vectors  and
and 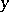 , with certain constants
, with certain constants  . Under additional restrictions (see [3]) on
. Under additional restrictions (see [3]) on 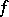 and by a special selection of
and by a special selection of 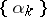 , the gradient method ensures the convergence of
, the gradient method ensures the convergence of  to a solution
to a solution 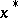 of the initial problem with the rate of an arithmetical progression with ratio
of the initial problem with the rate of an arithmetical progression with ratio 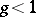 . A special case of the gradient method is the method of steepest descent (cf. Steepest descent, method of), in which the matrix
. A special case of the gradient method is the method of steepest descent (cf. Steepest descent, method of), in which the matrix 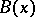 is the unit matrix.
is the unit matrix.
References
| [1] | L.V. Kantorovich, G.P. Akilov, "Functionalanalysis in normierten Räumen" , Akademie Verlag (1964) (Translated from Russian) |
| [2] | G. Zoutendijk, "Methods of feasible directions" , Elsevier (1970) |
| [3] | B.N. Pshenichnyi, Yu.M. Danilin, "Numerical methods in extremal problems" , MIR (1978) (Translated from Russian) |
| [4] | B.T. Polyak, "Gradient methods for the minimization of functionals" USSR Comp. Math. Math. Physics , 3 : 4 (1963) pp. 864–878 Zh. Vychisl. Mat. i Mat. Fiz. , 3 : 4 (1963) pp. 643–654 |
Comments
See also Coordinate-wise descent method.
References
| [a1] | J.M. Ortega, W.C. Rheinboldt, "Iterative solution of non-linear equations in several variables" , Acad. Press (1970) |
Descent, method of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Descent,_method_of&oldid=11500