Coordinate-wise descent method
One of the methods for minimizing a function of several variables based only on the values of the function to be minimized. The method is used when the function is not differentiable or if a calculation of the derivatives involves a large amount of computation. Below the use of the coordinate-wise descent method for minimizing a function 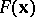 on a set
on a set
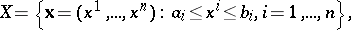 |
where 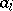 and
and 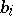 are given numbers,
are given numbers, 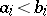 , is described and the cases where all or some of the
, is described and the cases where all or some of the 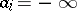 or
or 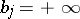 are not excluded. Let
are not excluded. Let 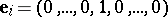 be the coordinate vector in which the
be the coordinate vector in which the 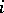 -th coordinate is equal to 1 and the other coordinates are equal to zero. One specifies an initial approximation
-th coordinate is equal to 1 and the other coordinates are equal to zero. One specifies an initial approximation 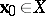 ,
, 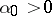 . Assume that the
. Assume that the  -th approximation
-th approximation 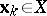 is known and that
is known and that 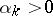 , for some
, for some 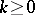 . Take
. Take 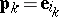 , where
, where 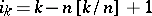 and
and 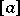 is the integer part of
is the integer part of  . Then
. Then
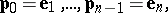 |
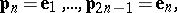 |
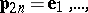 |
i.e. one performs a cyclic selection of the coordinate vectors  . First one checks if the conditions
. First one checks if the conditions
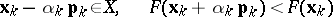 | (1) |
are fulfilled. If (1) is fulfilled, one sets  ,
, 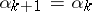 . If on the other hand (1) is not fulfilled, one checks the condition
. If on the other hand (1) is not fulfilled, one checks the condition
 | (2) |
If (2) is fulfilled, one sets 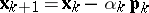 ,
,  . If conditions (1) and (2) are both not fulfilled, one sets
. If conditions (1) and (2) are both not fulfilled, one sets 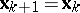 ,
,
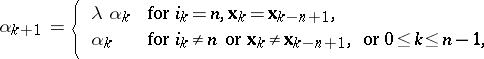 | (3) |
where 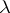 is the parameter of the method,
is the parameter of the method, 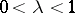 . Condition (3) means that if at least one of the conditions (1) and (2) is fulfilled in a single cycle of
. Condition (3) means that if at least one of the conditions (1) and (2) is fulfilled in a single cycle of  iterations involving a selection of all coordinate vectors
iterations involving a selection of all coordinate vectors  with step
with step 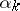 , then the length of the step
, then the length of the step 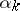 is not reduced and is retained at least during the following cycle of
is not reduced and is retained at least during the following cycle of  iterations; if on the other hand neither (1) nor (2) is ever fulfilled in the subsequent
iterations; if on the other hand neither (1) nor (2) is ever fulfilled in the subsequent  iterations, the step
iterations, the step  is reduced.
is reduced.
Let 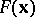 be convex and continuously differentiable on
be convex and continuously differentiable on  , let the set
, let the set 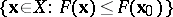 be bounded and let
be bounded and let 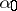 be a positive number. Then the methods (1)–(3) converge, i.e.
be a positive number. Then the methods (1)–(3) converge, i.e.
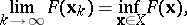 |
and the sequence 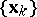 converges to the set of minima for
converges to the set of minima for 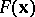 in
in  . If
. If 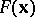 is not differentiable on
is not differentiable on  , the method need not converge [1], [2].
, the method need not converge [1], [2].
References
| [1] | F.P. Vasil'ev, "Numerical methods for solving extremum problems" , Moscow (1980) (In Russian) |
| [2] | V.G. Karmanov, "Mathematical programming" , Moscow (1975) (In Russian) |
Comments
References
| [a1] | W.I. Zangwill, "Nonlinear programming: a unified approach" , Prentice-Hall (1969) |
Coordinate-wise descent method. F.P. Vasil'ev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coordinate-wise_descent_method&oldid=18950