Cotorsion-free group
An Abelian group is cotorsion-free if it does not contain any non-zero cotorsion group. More explicitly, this means that it contains no subgroup isomorphic to the additive group  of rational numbers, or to the additive group of
of rational numbers, or to the additive group of  -adic integers for any prime
-adic integers for any prime  , and contains no cyclic group of prime order (thus, it is torsion-free). Equivalently, an Abelian group
, and contains no cyclic group of prime order (thus, it is torsion-free). Equivalently, an Abelian group  is cotorsion-free if and only if
is cotorsion-free if and only if  , where
, where  denotes the completion of the group
denotes the completion of the group  of integers in its
of integers in its  -adic topology. Cotorsion-free rings are rings (cf. Ring) whose additive groups are cotorsion-free Abelian groups. These rings play a distinguished role in the realization of rings as endomorphism rings of Abelian groups.
-adic topology. Cotorsion-free rings are rings (cf. Ring) whose additive groups are cotorsion-free Abelian groups. These rings play a distinguished role in the realization of rings as endomorphism rings of Abelian groups.
The celebrated theorem of Corner [a1] states that any countable cotorsion-free ring  with identity is isomorphic to the endomorphism ring of a countable reduced torsion-free Abelian group
with identity is isomorphic to the endomorphism ring of a countable reduced torsion-free Abelian group  . Moreover, if the additive group of
. Moreover, if the additive group of  has finite rank
has finite rank  , then
, then  can be chosen to have rank at most
can be chosen to have rank at most  . Corner's theorem has been generalized in various directions, notably to rings of arbitrary cardinality. The best result is due to R. Göbel and S. Shelah [a3]: Let
. Corner's theorem has been generalized in various directions, notably to rings of arbitrary cardinality. The best result is due to R. Göbel and S. Shelah [a3]: Let 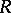 be a cotorsion-free ring with identity and
be a cotorsion-free ring with identity and  a cardinal number such that
a cardinal number such that  . There are
. There are 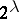 cotorsion-free groups
cotorsion-free groups  of cardinality
of cardinality  whose endomorphism rings are isomorphic to
whose endomorphism rings are isomorphic to  such that
such that 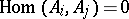 for
for 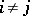 .
.
These results have several applications to the construction of counterexamples for torsion-free Abelian groups, e.g. to Kaplansky's test problems. Another consequence is the existence of arbitrarily large indecomposable Abelian groups. There is a topological version of the above theorem. If the endomorphism ring of an Abelian group  is equipped with the finite topology, then it becomes a complete Hausdorff topological ring (cf. also Hausdorff space). The Corner–Göbel theorem [a2] states that a topological ring
is equipped with the finite topology, then it becomes a complete Hausdorff topological ring (cf. also Hausdorff space). The Corner–Göbel theorem [a2] states that a topological ring  with identity is isomorphic to the finitely topologized endomorphism ring of a cotorsion-free Abelian group
with identity is isomorphic to the finitely topologized endomorphism ring of a cotorsion-free Abelian group  if and only if
if and only if  is complete Hausdorff in its topology and admits a base of neighbourhoods of
is complete Hausdorff in its topology and admits a base of neighbourhoods of  consisting of left ideals
consisting of left ideals  such that
such that  is cotorsion-free (the endomorphisms act on the left). The Göbel–Shelah theorem [a3] generalizes to cotorsion-free algebras over commutative domains. The proof relies on the most useful black box principle.
is cotorsion-free (the endomorphisms act on the left). The Göbel–Shelah theorem [a3] generalizes to cotorsion-free algebras over commutative domains. The proof relies on the most useful black box principle.
References
| [a1] | A.L.S. Corner, "Every countable reduced torsion-free ring is an endomorphism ring" Proc. London Math. Soc. , 13 (1963) pp. 687–710 |
| [a2] | A.L.S. Corner, R. Göbel, "Prescribing endomorphism algebras, a unified treatment" Proc. London Math. Soc. , 50 (1985) pp. 447–479 |
| [a3] | R. Göbel, S. Shelah, "Modules over arbitrary domains" Math. Z. , 188 (1985) pp. 325–337 |
Cotorsion-free group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cotorsion-free_group&oldid=18619