Convergence, types of
One of the basic concepts of mathematical analysis, signifying that a mathematical object has a limit. In this sense one speaks of the convergence of a sequence of elements, convergence of a series, convergence of an infinite product, convergence of a continued fraction, convergence of an integral, etc. The concept of convergence arises, for example, in the study of mathematical objects and their approximation by simpler objects. Thus, in order to calculate the area of a circle, a sequence of areas of regular polygons inscribed in this circle is used; for the approximate calculation of integrals of functions, approximations are used involving piecewise-linear functions or, more generally, splines (cf. Spline), etc. One can say that mathematical analysis begins at the moment when the concept of convergence has been introduced on a set of elements.
I. Convergence of sequences.
Various concepts of convergence of elements of a set can be applied to one and the same set of elements, depending on the problem under consideration. The concept of convergence plays an important role in the solution of various equations (algebraic, differential, integral, etc.) and particularly in finding approximate numerical solutions for them. For example, the method of sequential approximation (cf. Sequential approximation, method of) makes it possible to obtain a sequence of functions that converges to the solution of a given ordinary differential equation, and to thereby simultaneously prove, given specific conditions, the existence of a solution and to provide a method that makes it possible to calculate this solution with the required accuracy. Both for ordinary and partial differential equations there are various convergent difference methods for their numerical solution, which are suitable for use in modern computers.
If a concept of convergence of sequences of elements of a set 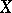 is introduced, i.e. a class is defined within the totality of all given sequences, every
is introduced, i.e. a class is defined within the totality of all given sequences, every  of which is said to be a convergent sequence, while every convergent sequence corresponds to a certain element of
of which is said to be a convergent sequence, while every convergent sequence corresponds to a certain element of 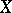 , called its limit, then the set
, called its limit, then the set 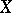 itself is called a space with convergence.
itself is called a space with convergence.
It is usually required of a concept of convergence of sequences that it possess the following properties:
1) every sequence of elements of 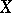 can have at most one limit;
can have at most one limit;
2) every stationary sequence 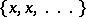 ,
, 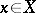 , is convergent and the element
, is convergent and the element  is its limit;
is its limit;
3) every subsequence of a convergent sequence is also convergent and has the same limit as the whole sequence.
When these conditions are fulfilled, the space 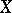 is often called a space with convergence in the sense of Fréchet. An example of such a space is any topological Hausdorff space, and consequently any metric space, especially any countably-normed space, and therefore any normed space (although by no means every semi-normed space). In order for a sequence to converge in a complete metric space it is necessary and sufficient that it be a fundamental sequence.
is often called a space with convergence in the sense of Fréchet. An example of such a space is any topological Hausdorff space, and consequently any metric space, especially any countably-normed space, and therefore any normed space (although by no means every semi-normed space). In order for a sequence to converge in a complete metric space it is necessary and sufficient that it be a fundamental sequence.
An example of a non-metrizable space with convergence in the sense of Fréchet is the space of all real functions defined on the number axis 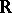 , where the convergence of a sequence
, where the convergence of a sequence 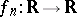 ,
, 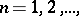 signifies its convergence for every fixed
signifies its convergence for every fixed 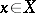 .
.
If for every subset  in the space
in the space 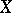 with convergence in the sense of Fréchet one defines the closure
with convergence in the sense of Fréchet one defines the closure 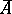 as the totality of all points of
as the totality of all points of 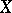 that are limits of sequences of points belonging to
that are limits of sequences of points belonging to 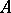 , then
, then 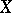 may prove not to be a topological space, since the closure
may prove not to be a topological space, since the closure 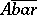 of the closure
of the closure 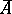 of every set
of every set 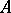 in the given definition need not coincide with
in the given definition need not coincide with 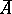 .
.
If two definitions of convergence are introduced on the same set, and if every sequence that converges in the sense of the first definition also converges in the sense of the second, then one says that the second convergence is stronger than the first. In every space  with convergence it is possible to introduce a stronger convergence such that the operation of closure thus generated makes
with convergence it is possible to introduce a stronger convergence such that the operation of closure thus generated makes 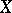 a topological space, or, more concisely, every space with convergence can be imbedded in a topological space consisting of the same points.
a topological space, or, more concisely, every space with convergence can be imbedded in a topological space consisting of the same points.
On every topological space, the concept of convergence of sequences of points of the space is defined, but this definition is insufficient, generally speaking, to describe the closure of an arbitrary set in this space, i.e. to define the points of contact of the set; consequently, it is insufficient to describe the topology of the given space completely. In order for this to be possible, the concept of a convergent generalized sequence is introduced.
A partially ordered set 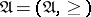 is called a directed set if for any two elements there is an element following both of them. A mapping
is called a directed set if for any two elements there is an element following both of them. A mapping 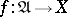 of a directed set
of a directed set 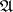 into a set
into a set 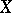 is called a generalized sequence, a net or a directionality in
is called a generalized sequence, a net or a directionality in 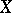 . A generalized sequence
. A generalized sequence 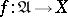 in a topological space
in a topological space 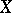 is said to be convergent to a point
is said to be convergent to a point 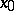 in
in 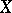 if for every neighbourhood
if for every neighbourhood  of
of 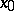 there is an
there is an 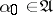 such that for all
such that for all 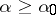 ,
,  , the inclusion
, the inclusion 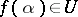 holds. In this case one says that the limit of the generalized sequence
holds. In this case one says that the limit of the generalized sequence 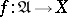 exists and is equal to
exists and is equal to 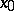 ; this is denoted by
; this is denoted by 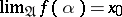 .
.
In these terms, the closure of a set lying in a topological space 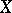 is described in the following way: In order for a point
is described in the following way: In order for a point  to belong to the closure
to belong to the closure  of a set
of a set 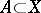 it is necessary and sufficient that a certain generalized sequence of points in
it is necessary and sufficient that a certain generalized sequence of points in 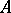 converges to
converges to  ; for a topological space to be a Hausdorff space, it is necessary and sufficient that every generalized sequence of points of it has at most one limit.
; for a topological space to be a Hausdorff space, it is necessary and sufficient that every generalized sequence of points of it has at most one limit.
In terms of convergence of generalized sequences, it is also possible to formulate a criterion for the continuity of a mapping 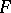 of a topological space
of a topological space 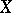 into a topological space
into a topological space 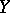 : For such a mapping
: For such a mapping 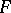 to be continuous at a point
to be continuous at a point 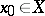 it is necessary and sufficient that for every generalized sequence
it is necessary and sufficient that for every generalized sequence 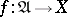 for which
for which 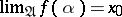 , the condition
, the condition 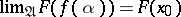 is fulfilled.
is fulfilled.
II. Convergence of sequences and series of numbers.
The simplest examples illustrating the concept of convergence are convergent sequences of numbers, i.e. sequences of complex numbers 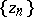 that have finite limits, and convergent series of numbers, i.e. series for which the sequence of partial sums converges. Convergent sequences and series of numbers are often used to obtain various estimates, while in numerical methods they are used for the approximate calculation of the values of functions and constants. In problems of this type, it is important to know the "rate" at which a given sequence converges to its limit. For example, the number
that have finite limits, and convergent series of numbers, i.e. series for which the sequence of partial sums converges. Convergent sequences and series of numbers are often used to obtain various estimates, while in numerical methods they are used for the approximate calculation of the values of functions and constants. In problems of this type, it is important to know the "rate" at which a given sequence converges to its limit. For example, the number 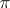 can be represented in the form of a sum of series in the following two ways:
can be represented in the form of a sum of series in the following two ways:
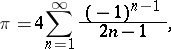 |
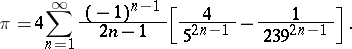 |
It is clear that for the approximate calculation of the number 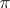 with a sufficient degree of accuracy, it is advisable to use the second formula (Machin's formula), since it is possible, using the second formula, to achieve the same degree of accuracy in the calculation using a smaller number of terms of the series.
with a sufficient degree of accuracy, it is advisable to use the second formula (Machin's formula), since it is possible, using the second formula, to achieve the same degree of accuracy in the calculation using a smaller number of terms of the series.
In order to compare the convergence of two series, the following definition is used. Let there be given two convergent series with non-negative terms
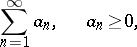 | (1) |
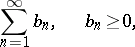 | (2) |
and let 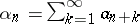 ,
,  be their remainders of order
be their remainders of order 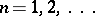 . The series (1) is said to converge faster than the series (2), or the series (2) is said to converge more slowly than the series (1), which is equivalent, if
. The series (1) is said to converge faster than the series (2), or the series (2) is said to converge more slowly than the series (1), which is equivalent, if 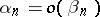 as
as 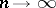 , i.e. if a null sequence
, i.e. if a null sequence 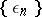 exists such that
exists such that 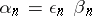 ,
,  .
.
If the series (1) and (2) are divergent and 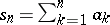 ,
,  are their partial sums of order
are their partial sums of order 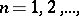 then (1) is said to diverge faster than (2), or (2) is said to diverge more slowly than (1), if
then (1) is said to diverge faster than (2), or (2) is said to diverge more slowly than (1), if 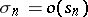 as
as 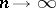 .
.
For every convergent series with non-negative terms there is a series, also with non-negative terms, that converges more slowly, while for every divergent series, there is one that diverges more slowly. Methods exist that make it possible to transform a given convergent series into one that converges faster without altering its sum. This can be done using, for example, the Abel transformation.
In addition to the ordinary concept of the sum of a series, indicated above, there are other, more general definitions of its sum, which are based on different methods of summation of series. By these methods some sequences consisting of the terms of a series are constructed instead of the sequence of partial sums. These sequences can be convergent in cases where the sequence of partial sums is divergent. The limits of these sequences are called generalized sums of the series.
The concept of faster convergence and divergence is also used for improper integrals, where one of the most widespread methods of acceleration of convergence (divergence) of integrals is the method of integration by parts. There are also other methods of averaging improper integrals that are analogous to methods of summation of series, and that make it possible to give a definition of generalized convergence for certain divergent integrals.
III. Convergence of series and sequences of functions.
In the case of sequences of functions
 | (3) |
under corresponding assumptions on the sets 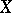 and
and 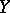 , various concepts of convergence exist illustrating the wide variety of concrete realizations of this concept. If
, various concepts of convergence exist illustrating the wide variety of concrete realizations of this concept. If 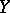 is a topological space, and if the sequence (3) converges for every fixed
is a topological space, and if the sequence (3) converges for every fixed 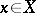 , then it is said to be (pointwise) convergent on the set
, then it is said to be (pointwise) convergent on the set 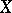 . If
. If 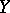 is a uniform space (in particular, a metric space or a topological group), then it is possible to introduce the concept of a uniformly-convergent sequence (see Uniform convergence).
is a uniform space (in particular, a metric space or a topological group), then it is possible to introduce the concept of a uniformly-convergent sequence (see Uniform convergence).
Let 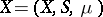 be a measure space (i.e.
be a measure space (i.e. 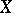 a set,
a set, 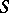 a
a  -algebra of subsets of
-algebra of subsets of 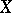 , and
, and 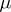 a real-valued measure on
a real-valued measure on 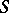 ), let
), let 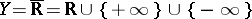 be the extended set of real numbers
be the extended set of real numbers 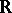 , and let the functions
, and let the functions
 | (4) |
be almost-everywhere finite and measurable.
The sequence (4) is said to be almost-everywhere convergent to a function 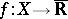 if there exists a set
if there exists a set 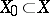 of measure zero such that the restrictions of the functions (4) to
of measure zero such that the restrictions of the functions (4) to 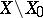 converge on this set to the restriction of
converge on this set to the restriction of  to it. If the sequence (4) converges almost-everywhere to a function
to it. If the sequence (4) converges almost-everywhere to a function 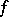 , then this function is also almost-everywhere finite and measurable. The link between almost-everywhere convergence of a sequence and uniform convergence is established by the Egorov theorem.
, then this function is also almost-everywhere finite and measurable. The link between almost-everywhere convergence of a sequence and uniform convergence is established by the Egorov theorem.
The sequence (4) is said to converge in measure on the set 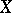 to a measurable function
to a measurable function  if, for any
if, for any 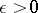 , the condition
, the condition
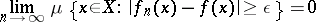 |
is fulfilled.
If the sequence (4) converges almost-everywhere to a function  and
and  , then it converges to
, then it converges to 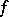 in measure as well, while if the sequence (4) converges to
in measure as well, while if the sequence (4) converges to 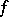 in measure, then there exists a subsequence of (4) that converges to
in measure, then there exists a subsequence of (4) that converges to 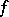 almost-everywhere.
almost-everywhere.
For a function 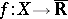 , let
, let
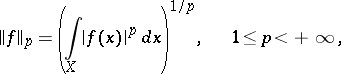 | (5) |
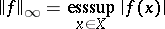 | (6) |
and let 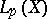 be the space of functions
be the space of functions 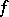 for which
for which
 | (7) |
These spaces are usually called Lebesgue spaces. On equivalence classes relative to the measure 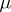 of functions for which condition (7) is fulfilled, the functional
of functions for which condition (7) is fulfilled, the functional 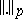 is a norm (see Convergence in norm).
is a norm (see Convergence in norm).
If the sequence (4) converges in the norm (6) to a function, then it converges to this function almost-everywhere. If a sequence 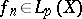 ,
, 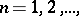 converges in the norm
converges in the norm 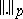 ,
, 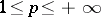 , to a function
, to a function 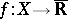 , then
, then 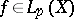 and the given sequence is said to be convergent to
and the given sequence is said to be convergent to 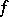 in the space
in the space 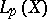 . Convergence in the norm
. Convergence in the norm 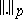 ,
, 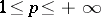 , is also called strong convergence in the space
, is also called strong convergence in the space 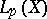 , or, when
, or, when 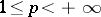 , convergence in the mean of order
, convergence in the mean of order 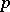 ; in more detail, when
; in more detail, when 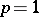 , it is called convergence in the mean, and when
, it is called convergence in the mean, and when 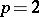 , convergence in the sense of the quadratic mean. An example of sequences of functions converging in the sense of the quadratic mean are sequences of partial sums of Fourier series of functions belonging to the space
, convergence in the sense of the quadratic mean. An example of sequences of functions converging in the sense of the quadratic mean are sequences of partial sums of Fourier series of functions belonging to the space 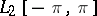 .
.
If the sequence (4) converges in 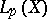 ,
, 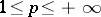 , to a function
, to a function  , then it converges to
, then it converges to 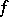 on the set
on the set 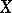 in measure as well, and it is therefore possible to extract a subsequence from (4) that will converge to
in measure as well, and it is therefore possible to extract a subsequence from (4) that will converge to 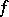 almost-everywhere on
almost-everywhere on 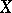 . If
. If 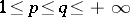 , if
, if 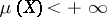 and if the sequence (4) converges in
and if the sequence (4) converges in 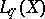 , then it also converges in
, then it also converges in 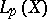 .
.
A sequence (4) of functions 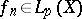 ,
,  , is said to be weakly convergent in
, is said to be weakly convergent in  to a function
to a function 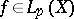 if for every function
if for every function 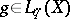 , where
, where 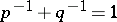 ,
,
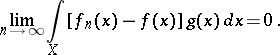 |
If a sequence 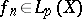 ,
, 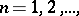 converges strongly in
converges strongly in 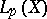 ,
, 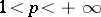 , then it also converges weakly to the same function; but there exist weakly-convergent sequences in
, then it also converges weakly to the same function; but there exist weakly-convergent sequences in 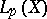 that do not converge strongly. For example, the sequence of functions
that do not converge strongly. For example, the sequence of functions 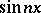 ,
, 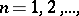 converges weakly to zero in
converges weakly to zero in 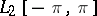 , but does not converge strongly. In fact, for every function
, but does not converge strongly. In fact, for every function 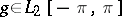 the integrals
the integrals
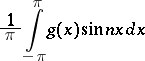 |
are the Fourier coefficients of 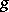 with respect to the system
with respect to the system 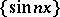 and therefore tend to zero as
and therefore tend to zero as 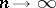 ; however,
; however, 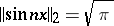 ,
, 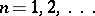 .
.
The limits of sequences of functions that converge almost-everywhere, or in measure, or in the sense of strong or weak convergence in 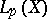 , are, in the case of a complete measure
, are, in the case of a complete measure  , defined uniquely up to functions that are equivalent relative to
, defined uniquely up to functions that are equivalent relative to  .
.
Generalizations of the Lebesgue space 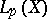 include the spaces of Nikol'skii, Sobolev, Orlicz (cf. Nikol'skii space; Orlicz space; Sobolev space), and a number of others.
include the spaces of Nikol'skii, Sobolev, Orlicz (cf. Nikol'skii space; Orlicz space; Sobolev space), and a number of others.
The concept of strong and weak convergence can be generalized to include more general spaces, in particular normed linear spaces.
Other concepts of convergence of a sequence of functions arise in the theory of generalized functions. For example, let 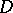 be the space of test functions, which consists of infinitely-differentiable functions
be the space of test functions, which consists of infinitely-differentiable functions 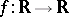 with compact support. A sequence
with compact support. A sequence 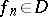 ,
, 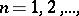 is said to be convergent to
is said to be convergent to 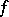 in the space
in the space 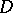 if there exists an interval
if there exists an interval 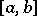 such that the supports of all functions
such that the supports of all functions 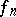 ,
, 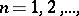 and
and 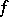 are contained in it, while the sequences
are contained in it, while the sequences 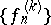 of the functions
of the functions 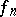 themselves and all their derivatives converge uniformly on
themselves and all their derivatives converge uniformly on 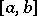 respectively to
respectively to 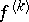 ,
, 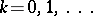 . In the study of the Fourier transforms of generalized functions, other spaces of test functions with convergence are examined.
. In the study of the Fourier transforms of generalized functions, other spaces of test functions with convergence are examined.
The different forms of convergence listed above are used in studying various questions of mathematical analysis. Thus, the concept of uniform convergence makes it possible to formulate conditions under which continuity is retained in a limit transition. For example, if 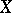 is a topological space and
is a topological space and 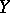 is a metric space, if the terms of the sequence (3) are continuous on
is a metric space, if the terms of the sequence (3) are continuous on  , and the sequence (3) converges uniformly on
, and the sequence (3) converges uniformly on 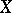 , then the limit function is also continuous on
, then the limit function is also continuous on 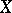 . In terms of the concept of almost-everywhere convergence or convergence in the mean of order
. In terms of the concept of almost-everywhere convergence or convergence in the mean of order 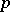 , it is possible to formulate conditions for limit transition under the integral sign. If
, it is possible to formulate conditions for limit transition under the integral sign. If 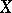 is a space with a measure
is a space with a measure 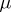 , if
, if 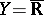 , if the sequence
, if the sequence 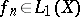 ,
, 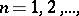 converges almost-everywhere on
converges almost-everywhere on 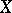 , and if a function
, and if a function 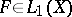 exists such that for almost-all
exists such that for almost-all 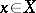 and all
and all 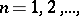 the inequality
the inequality 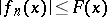 is fulfilled, then
is fulfilled, then
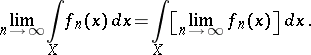 | (8) |
If 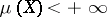 ,
, 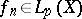 ,
, 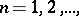
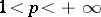 , and if the sequence
, and if the sequence 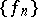 converges weakly (strongly) in
converges weakly (strongly) in 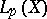 , then formula (8) holds.
, then formula (8) holds.
In probability theory one uses for sequences of random variables the phrase "almost-sure convergencealmost-certain convergence28A20almost-certain (or almost-sure) convergence" (convergence with probability one, cf. Convergence, almost-certain), for almost-everywhere convergence; convergence in probability, for convergence in measure; and the concept of convergence in distribution.
A generalization of the concept of convergence of a sequence of functions is convergence with respect to a certain parameter of a family of functions belonging to a certain topological space.
Mathematicians in ancient times (Euclid, Archimedes) used the concept of convergence in using series to find areas and volumes. They reasoned that by the method of exhaustion, they could prove the convergence of series. The term "convergence" was introduced in the context of series in 1668 by J. Gregory in his research on the methods of calculating the area of a disc and of a hyperbolic sector. Mathematicians in the 17th century usually had a fairly clear picture of the convergence of the series they used, but they could not produce proofs of this convergence that are strict in the modern sense. In the 18th century, the deliberate use of divergent series became widespread in mathematical analysis (especially in the work of L. Euler). This resulted, on the one hand, in many misunderstandings and errors which were not eliminated until a clear theory of convergence was developed, and on the other hand, in an early version of the modern theory of summation of divergent series. Strict methods for studying the convergence of series were worked out in the 19th century by A.L. Cauchy, N.H. Abel, B. Bolzano, K. Weierstrass, and others. The concept of uniform convergence was formulated in the work of Abel (1826), P. Seidel (1847–1848), G. Stokes (1847–1848) and Cauchy (1853), and began to be used systematically in Weierstrass' lectures on mathematical analysis in the late 1850's. Further extensions of the concept of convergence arose in the development of function theory, functional analysis and topology.
References
| [1] | P.S. [P.S. Aleksandrov] Aleksandroff, "Einführung in die Mengenlehre und in die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [3] | J.L. Kelley, "General topology" , Springer (1975) |
| [4] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [5] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1–2 , Moscow (1981) (In Russian) |
| [6] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
Comments
The statement under which (8) is fulfilled is generally known as Lebesgue's dominated convergence theorem.
For the notion of fundamental sequence see Cauchy sequence.
A null sequence is a sequence converging to zero. The essential supremum of a non-negative measurable function  (
(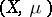 a measure space) is the infimum of the set
a measure space) is the infimum of the set 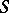 of all
of all 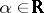 such that
such that
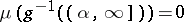 |
(if 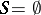 , one puts
, one puts 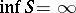 ). The essential supremum,
). The essential supremum, 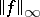 , of an arbitrary (complex-valued) measurable function
, of an arbitrary (complex-valued) measurable function 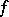 on
on 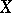 is the essential supremum of
is the essential supremum of 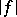 (cf. [a2]).
(cf. [a2]).
References
| [a1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [a2] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24 |
Convergence, types of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convergence,_types_of&oldid=18194