Continuous function
A basic concept in mathematical analysis.
Let 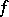 be a real-valued function defined on a subset
be a real-valued function defined on a subset 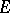 of the real numbers
of the real numbers 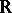 , that is,
, that is, 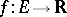 . Then
. Then 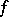 is said to be continuous at a point
is said to be continuous at a point  (or, in more detail, continuous at
(or, in more detail, continuous at 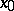 with respect to
with respect to 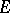 ) if for any
) if for any 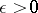 there exists a
there exists a 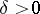 such that for all
such that for all 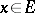 with
with 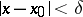 the inequality
the inequality
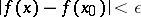 |
is valid. If one denotes by
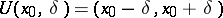 |
and
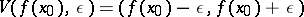 |
the 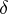 - and
- and  -neighbourhoods of
-neighbourhoods of  and
and 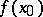 , respectively, then the definition above can be rephrased as follows:
, respectively, then the definition above can be rephrased as follows: 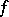 is called continuous at a point
is called continuous at a point  if for each
if for each  -neighbourhood
-neighbourhood  of
of 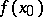 there is a
there is a 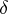 -neighbourhood
-neighbourhood 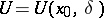 of
of 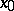 such that
such that 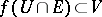 .
.
By using the concept of a limit one can say that 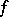 is continuous at a point
is continuous at a point 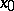 if its limit with respect to the set
if its limit with respect to the set 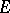 exists at that point and if this limit is equal to
exists at that point and if this limit is equal to 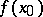 :
:
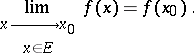 |
This is equivalent to
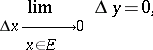 |
where 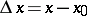 ,
, 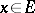 , and
, and 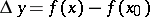 ; that is, to an infinitely small increment of the argument at
; that is, to an infinitely small increment of the argument at 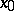 corresponds an infinitely small increment of the function.
corresponds an infinitely small increment of the function.
In terms of the limit of a sequence, the definition of continuity of a function at 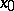 is:
is: 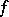 is continuous at
is continuous at 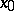 if for every sequence of points
if for every sequence of points 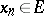 ,
, 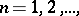 for which
for which 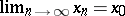 , one has
, one has
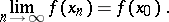 |
All these definitions of a function being continuous at a point are equivalent.
If 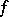 is continuous at
is continuous at 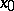 with respect to the set
with respect to the set 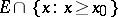 (or
(or 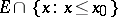 ), then
), then 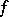 is said to be continuous on the right (or left) at
is said to be continuous on the right (or left) at 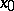 .
.
All basic elementary functions are continuous at all points of their domains of definition. An important property of continuous functions is that their class is closed under the arithmetic operations and under composition of functions. More accurately, if two real-valued functions 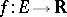 and
and 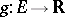 ,
,  , are continuous at
, are continuous at 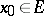 , then so is their sum
, then so is their sum 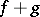 , difference
, difference 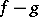 and product
and product 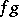 , and when
, and when 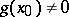 , also their quotient
, also their quotient 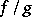 (which is necessarily defined in the intersection of
(which is necessarily defined in the intersection of 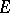 with a certain neighbourhood of
with a certain neighbourhood of 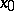 ). If, as before,
). If, as before,  is continuous at
is continuous at 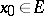 and
and 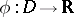 ,
, 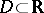 , is such that
, is such that 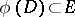 , so that the composite
, so that the composite 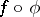 makes sense, if there is a
makes sense, if there is a 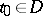 such that
such that 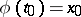 and if
and if 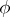 is continuous at
is continuous at 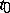 , then
, then 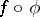 is also continuous at
is also continuous at 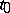 . Thus, in this case
. Thus, in this case
 |
that is, in this sense the operation of limit transition commutes with the operation of applying a continuous function. From these properties of continuous functions it follows that not only the basic, but also arbitrary elementary functions are continuous in their domains of definition. The property of continuity is also preserved under a uniform limit transition: If a sequence of functions  converges uniformly on a set
converges uniformly on a set 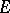 and if every
and if every 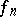 is continuous at
is continuous at 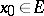 ,
, 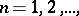 then
then
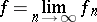 |
is continuous at 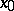 .
.
If a function 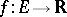 is continuous at every point of
is continuous at every point of 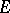 , then
, then 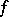 is said to be continuous on the set
is said to be continuous on the set 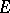 . If
. If 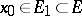 and
and 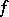 is continuous at
is continuous at 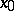 , then the restriction of
, then the restriction of 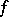 to
to 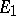 is also continuous at
is also continuous at 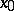 . The converse is not true, in general. For example, the restriction of the Dirichlet function either to the set of rational numbers or to the set of irrational numbers is continuous, but the Dirichlet function itself is discontinuous at all points.
. The converse is not true, in general. For example, the restriction of the Dirichlet function either to the set of rational numbers or to the set of irrational numbers is continuous, but the Dirichlet function itself is discontinuous at all points.
An important class of real-valued continuous functions of a single variable consists of those functions that are continuous on intervals. They have the following properties.
Weierstrass' first theorem: A function that is continuous on a closed interval is bounded on that interval.
Weierstrass' second theorem: A function that is continuous on a closed interval assumes on that interval a largest and a smallest value.
Cauchy's intermediate value theorem: A function that is continuous on a closed interval assumes on it any value between those at the end points.
The inverse function theorem: If a function is continuous and strictly monotone on an interval, then it has a single-valued inverse function, which is also defined on an interval and is strictly monotone and continuous on it.
Cantor's theorem on uniform continuity: A function that is continuous on a closed interval is uniformly continuous on it.
Every function that is continuous on a closed interval can be uniformly approximated on it with arbitrary accuracy by an algebraic polynomial, and every function  that is continuous on
that is continuous on 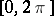 and is such that
and is such that 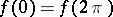 can be uniformly approximated on
can be uniformly approximated on 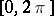 with arbitrary accuracy by trigonometric polynomials (see Weierstrass theorem on the approximation of functions).
with arbitrary accuracy by trigonometric polynomials (see Weierstrass theorem on the approximation of functions).
The concept of a continuous function can be generalized to wider forms of functions, above all, to functions of several variables. The definition above is preserved formally if one understands by 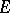 a subset of an
a subset of an  -dimensional Euclidean space
-dimensional Euclidean space 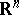 , by
, by 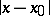 the distance between two points
the distance between two points 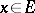 and
and 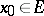 , by
, by 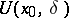 the
the 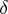 -neighbourhood of
-neighbourhood of 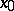 in
in 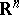 , and by
, and by
 |
the limit of a sequence of points in 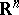 . A function
. A function 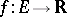 ,
, 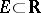 , of several variables
, of several variables  that is continuous at a point
that is continuous at a point  is also called continuous at this point
is also called continuous at this point 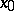 jointly in the variables
jointly in the variables  , in contrast to functions of several variables that are continuous in the variables individually. A function
, in contrast to functions of several variables that are continuous in the variables individually. A function 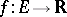 ,
, 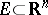 , is called continuous at a point
, is called continuous at a point 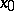 in, say, the variable
in, say, the variable 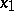 if the restriction of
if the restriction of 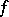 to the set
to the set
 |
is continuous at 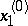 , that is, if the function
, that is, if the function 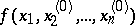 of the single variable
of the single variable 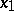 is continuous at
is continuous at 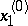 . A function
. A function 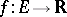 ,
, 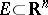 ,
, 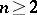 , can be continuous at
, can be continuous at  in every variable
in every variable  , but need not be continuous at this point jointly in the variables.
, but need not be continuous at this point jointly in the variables.
The definition of a continuous function goes over directly to complex-valued functions. Only one has to interpret  in the definition above as the norm of the complex number
in the definition above as the norm of the complex number 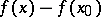 and
and
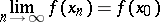 |
as the limit in the complex plane.
All these definitions are special cases of the more general concept of a continuous function 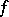 with as domain of definition a certain topological space
with as domain of definition a certain topological space 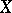 and with values in a certain topological space
and with values in a certain topological space 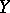 (see Continuous mapping).
(see Continuous mapping).
Many properties of real-valued continuous functions of a single variable carry over to continuous mappings between topological spaces. A generalization of Weierstrass' theorem mentioned above: The continuous image of a compact topological space in a Hausdorff space is compact. A generalization of Cauchy's intermediate value theorem for a continuous function on a closed interval: A continuous image of a connected topological space in a topological space is also connected. A generalization of the theorem on the inverse function of a strictly monotone continuous function: A continuous one-to-one mapping of a compactum onto a Hausdorff space is a homeomorphism. A generalization of the theorem on the limit of a uniformly-convergent sequence of continuous functions: If 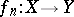 is a uniformly-convergent sequence of mappings of a topological space
is a uniformly-convergent sequence of mappings of a topological space 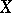 into a metric space
into a metric space 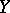 that are continuous (at a point
that are continuous (at a point 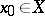 ) then the limit mapping
) then the limit mapping 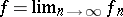 is also continuous (at
is also continuous (at 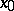 ). A generalization of Weierstrass' theorem on the approximation of functions that are continuous on a closed interval is the Stone–Weierstrass theorem.
). A generalization of Weierstrass' theorem on the approximation of functions that are continuous on a closed interval is the Stone–Weierstrass theorem.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [4] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
Comments
The topics discussed above can be found in almost any introductory book on real analysis. Proofs of all statements can be found in, e.g., [a5], Chapt. 3.
References
| [a1] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1957) |
| [a2] | R.G. Bartle, "The elements of real analysis" , Wiley (1976) |
| [a3] | G.H. Hardy, "A course of pure mathematics" , Cambridge Univ. Press (1975) |
| [a4] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 75–78 |
| [a5] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
| [a6] | R.P Boas jr., "A primer of real functions" , Math. Assoc. Amer. (1960) |
Continuous function. L.D. Kudryavtsev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_function&oldid=15327