Colombeau generalized function algebras
Let  be an open subset of
be an open subset of 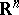 , and let
, and let 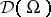 be the algebra of compactly supported smooth functions. In the original definition, J.F. Colombeau [a2] started from the space
be the algebra of compactly supported smooth functions. In the original definition, J.F. Colombeau [a2] started from the space 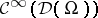 of infinitely Silva-differentiable mappings from
of infinitely Silva-differentiable mappings from 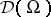 into
into 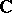 . The space of distributions
. The space of distributions 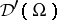 is just the subspace of linear mappings
is just the subspace of linear mappings 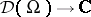 . Let
. Let
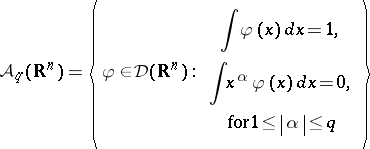 |
and let
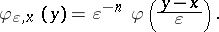 |
The subalgebra 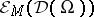 is defined by those members
is defined by those members  such that for all compact subsets
such that for all compact subsets  and for all multi-indices
and for all multi-indices 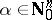 there is an
there is an 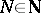 such that for all
such that for all 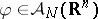 , the supremum of
, the supremum of 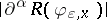 over
over 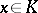 is of order
is of order 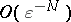 as
as 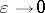 . The ideal
. The ideal 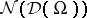 is defined by those members
is defined by those members 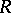 such that for all compact subsets
such that for all compact subsets 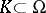 and all
and all 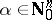 there is an
there is an 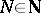 such that for all
such that for all 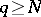 and
and 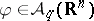 , the supremum of
, the supremum of 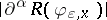 over
over 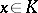 is of order
is of order 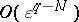 as
as 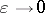 . The Colombeau generalized function algebra is the factor algebra
. The Colombeau generalized function algebra is the factor algebra  . It contains the space of distributions
. It contains the space of distributions 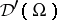 with derivatives faithfully extended (cf. also Generalized function, derivative of a). The asymptotic decay property expressed in
with derivatives faithfully extended (cf. also Generalized function, derivative of a). The asymptotic decay property expressed in 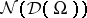 together with an argument using Taylor expansion shows that
together with an argument using Taylor expansion shows that 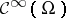 is a faithful subalgebra.
is a faithful subalgebra.
Later, Colombeau [a3], [a4] replaced the construction by a reduced power of 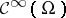 with index set
with index set 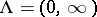 : Let
: Let 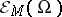 be the algebra of all nets
be the algebra of all nets  such that for all compact subsets
such that for all compact subsets 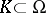 and all multi-indices
and all multi-indices 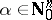 there is an
there is an 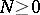 such that the supremum of
such that the supremum of 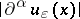 over
over 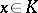 is of order
is of order  as
as 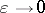 (cf. also Net (directed set)). Let
(cf. also Net (directed set)). Let  be the ideal therein given by those
be the ideal therein given by those 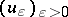 such that for all compact subsets
such that for all compact subsets 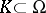 , all
, all 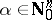 and all
and all 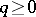 , the supremum of
, the supremum of 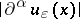 over
over 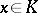 is of order
is of order 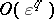 as
as 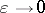 . Then set
. Then set 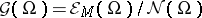 . There exist versions with the infinite-order Sobolev space
. There exist versions with the infinite-order Sobolev space 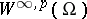 in the place of
in the place of 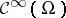 ,
, 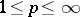 , or with other topological algebras.
, or with other topological algebras.
It is possible to enlarge the class of mollifiers (hence the index set 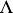 in the reduced power construction) to produce a version for which smooth coordinate changes commute with the imbedding of distributions. This way Colombeau generalized functions can be defined intrinsically on manifolds. Generalized stochastic processes with paths in
in the reduced power construction) to produce a version for which smooth coordinate changes commute with the imbedding of distributions. This way Colombeau generalized functions can be defined intrinsically on manifolds. Generalized stochastic processes with paths in 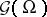 have been introduced as well.
have been introduced as well.
The subalgebra 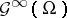 is defined by interchanging quantifiers: For all compact sets
is defined by interchanging quantifiers: For all compact sets 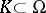 there is an
there is an  such that for all
such that for all 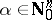 , the supremum of
, the supremum of 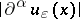 on
on 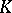 is of order
is of order 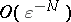 as
as 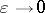 . One has that
. One has that 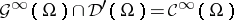 , and
, and 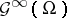 plays the same role in regularity theory here as
plays the same role in regularity theory here as 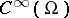 does in distribution theory (for example,
does in distribution theory (for example, 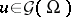 and
and 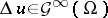 implies
implies 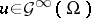 , where
, where 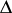 denotes the Laplace operator).
denotes the Laplace operator).
For applications in a variety of fields of non-linear analysis and physics, see [a1], [a4], [a5], [a6], [a7].
See also Generalized function algebras.
References
| [a1] | H.A. Biagioni, "A nonlinear theory of generalized functions" , Springer (1990) |
| [a2] | J.F. Colombeau, "New generalized functions and multiplication of distributions" , North-Holland (1984) |
| [a3] | J.F. Colombeau, "Elementary introduction to new generalized functions" , North-Holland (1985) |
| [a4] | J.F. Colombeau, "Multiplication of distributions. A tool in mathematics, numerical engineering and theoretical physics" , Springer (1992) |
| [a5] | "Nonlinear theory of generalized functions" M. Grosser (ed.) G. Hörmann (ed.) M. Kunzinger (ed.) M. Oberguggenberger (ed.) , Chapman and Hall/CRC (1999) |
| [a6] | M. Nedeljkov, S. Pilipović, D. Scarpalézos, "The linear theory of Colombeau generalized functions" , Longman (1998) |
| [a7] | M. Oberguggenberger, "Multiplication of distributions and applications to partial differential equations" , Longman (1992) |
Colombeau generalized function algebras. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Colombeau_generalized_function_algebras&oldid=17873