Code with correction of arithmetical errors

code for correction of arithmetic errors, code that corrects arithmetic errors, arithmetic code

A code intended for the control of the functioning of an adder. When adding numbers represented in the binary number system, a single slip in the functioning of the adder leads, as a rule, to a change in the result by some power of 2. In this connection, a (single) arithmetic error in the ring of integers $\mathbf Z$ is defined as a transformation of a number $N$ to a number $N ^ { \prime } = N \pm 2 ^ {i}$, $i = 0, 1 , . . .$. The function $\rho ( N _ {1} , N _ {2} )$ on $\mathbf Z \times \mathbf Z$, defined as the minimum number of arithmetic errors taking $N _ {1}$ to $N _ {2}$, is a metric. An arbitrary finite subset (a code) $K \subset \mathbf Z$ is characterized by its minimum distance

$$\rho ( K) = \ \min \rho ( N _ {1} , N _ {2} ),$$

where the minimum is taken over all distinct $N _ {1} , N _ {2} \in K$. The sets of $t$ or fewer arithmetic errors transform a number $N$ into a metric ball of radius $t$ and centre $N$. Therefore if the metric balls of radius $t$ described around any two numbers of a code do not intersect (that is, if the minimum distance of the code is greater than $2t$), then the code is said to be a code that corrects $t$ arithmetic errors. If the metric ball of radius $s$ described around any number of the code contains no other numbers of the code (that is, if the minimum distance of the code is greater than $s$), then the code is called a code that detects $s$ arithmetic errors. The metric $\rho$ has the following alternative description:

$$\rho ( N _ {1} , N _ {2} ) = \ w ( N _ {1} - N _ {2} ),$$

where $w ( N)$ is the (arithmetic) weight of $N$, i.e. the smallest possible number of non-zero coefficients in the representations

$$\tag{* } N = \sum _ {i = 0 } ^ { k } N _ {i} 2 ^ {i} ,\ \ N _ {i} = 0, \pm 1; \ \ k = 0, 1 , . . . .$$

For each $N$ there is a unique representation (*) on which $N _ {k} \neq 0$, $N _ {i} N _ {i + 1 } = 0$, $i = 0 \dots k - 1$, and the number of non-zero coefficients in the representation is $w ( N)$. For example, $23 = 2 ^ {4} + 2 ^ {2} + 2 ^ {1} + 2 ^ {0} = 2 ^ {5} - 2 ^ {3} - 2 ^ {0}$ and $w ( 23) = 3$. Since $\rho ( N _ {1} + N, N _ {2} + N) = \rho ( N _ {1} , N _ {2} )$ for any $N _ {1} , N _ {2} , N \in \mathbf Z$, one restricts attention to codes that do not contain negative numbers. By the length of a code $K$ one means the quantity $[ \mathop{\rm log} _ {2} B ( K)] + 1$, where $B ( K)$ is the largest number of the code $K$. There corresponds to an arbitrary number $B$ of a code of length $n$ a unique word $\beta ( B) = b _ {n - 1 } \dots b _ {0}$ over the alphabet $\{ 0, 1 \}$ such that $B = \sum _ {i = 0 } ^ {n - 1 } b _ {i} 2 ^ {i}$. If the code $K \subset \mathbf Z$ corrects $t$ arithmetic errors, then the code $\{ {\beta ( B) } : {B \in K } \}$ corrects $t$ errors (of substitution type) by virtue of the fact that $d ( \beta ( B _ {1} ), \beta ( B _ {2} )) \geq \rho ( B _ {1} , B _ {2} )$, where $d ( \cdot , \cdot )$ is the Hamming metric (see Error-correcting code). In the study of problems of control of an adder one usually considers an encoding $f: \{ 0 \dots M - 1 \} \rightarrow \mathbf Z$( see Coding and decoding) such that $f ( i + j) = f ( i) + f ( j)$ for $i + j < M$( which is equivalent to $f ( i) = A \cdot i$, where $A = f ( 1)$). In this case, the coding operation consists in the multiplication of the number to be encoded by $A$, while the detection of errors in the functioning of the adder consists in verifying that the result of the addition is divisible by $A$. The code $K _ {A,M} = \{ 0, A \dots A ( M - 1) \}$ is called an $AM$- code. The minimum distance of an $AM$- code is the minimum of the $w ( A \cdot i)$, $i = 1 \dots M - 1$. For example, the minimum distance of a $3M$- code is equal to 2; the code detects single arithmetic errors and is often applied in computers (in the form of a control modulo 3). The best studied are (cyclic and negacyclic) $AM$- codes with $M = ( 2 ^ {n} \pm 1)/A$; they are characterized by the property that whenever the number $B = \sum _ {i = 0 } ^ {n - 1 } b _ {i} 2 ^ {i}$, $b _ {i} = 0, 1$, belongs to the code, then so does the number $B ^ { \prime } = \pm b _ {n - 1 } + \sum _ {i = 1 } ^ {n - 1 } b _ {i} 2 ^ {i}$. Such codes, called $( n, A)$- codes, can be conveniently regarded as subsets of the metric space $\mathbf N _ {m} = \{ {0 \dots m - 1 } : {m = 2 ^ {n} \pm 1 } \}$, with metric $\rho _ {m} ( x, y) = w _ {m} ( x - y) = \min \{ w ( x - y), w ( x - y - m) \}$. The minimum distances of an $( n, A)$- code in the metrics $\rho$ and $\rho _ {m}$ are equal. To each $( n, A)$- code there is associated the $( n, A ^ {*} )$- code where $AA ^ {*} = m$; it is called the dual code. If 2 or $- 2$ are primitive roots modulo a prime number $p$, then the $(( p - 1)/2, p)$- code corrects single arithmetic errors and is perfect in the metric $\rho _ {m}$, that is, the metric balls of radius 1 described around the numbers of the code are not only pairwise disjoint but also fill out the whole of $\mathbf N _ {m}$. In the dual code, all distances between different numbers of the code are equal to $\left ] ( p + 1)/6 \right [$. The results listed above for codes are analogues of results for binary linear cyclic error-correcting codes. Meanwhile, there are no known arithmetic analogues of B.C.H. (Bose–Chaudhury–Hocquenghem)-codes; nor are there any known upper bounds for the size of codes with given length and distance, analogous to the best bound for error-correcting codes. Codes correcting $q$- ary arithmetic errors $( q > 2)$ possess even more characteristics (a $q$- ary arithmetical error is a transformation of a number $N$ to a number $N ^ { \prime } = N \pm aq ^ {i}$, $a = 1 \dots q - 1$; $i = 0, 1 , . . .$). Interest in such codes has increased with the development of computing techniques. Thus, in contrast to error-correcting codes, there are no perfect $AM$- codes with $q = 2 ^ {l}$( $l > 1$) that correct single $q$- ary arithmetic errors; for $q = 6$ there are examples known of such codes. Existence conditions for perfect $AM$- codes are of a number-theoretic character and are connected with the study of reciprocity laws in number fields.

References

[1]	Yu.G. Dadaev, "The theory of arithmetic codes" , Moscow (1981) (In Russian)
[2]	E. Weldon jr., "Error-correcting codes" , M.I.T. (1972)
[3]	J.L. Massey, O.N. Garcia, , Advances in information systems science , 4 , New York-London (1972) pp. 273–326
[4]	I.M. Boyarinov, G.A. Kabatyanskii, "Perfect single-error-correcting arithmetic 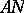-codes" Problemy Peredachi Informatsii , 12 : 1 (1976) pp. 16–23 (In Russian)