Category
A concept formalizing a number of algebraic properties of collections of morphism between mathematical objects of the same type (sets, topological spaces, groups, etc.) under the condition that these collections contain the identity mappings and are closed with respect to successive composition (or product) of mappings. A category 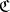 consists of a class
consists of a class 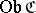 , whose elements are called objects of the category, and a class
, whose elements are called objects of the category, and a class 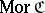 , the elements of which are called morphisms of the category. These classes must satisfy the following conditions:
, the elements of which are called morphisms of the category. These classes must satisfy the following conditions:
1) to each ordered pair of objects 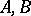 is associated a set
is associated a set 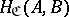 (also denoted by
(also denoted by 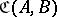 ,
,  , or
, or 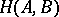 ) of members of
) of members of 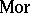 . If
. If 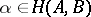 , then
, then 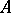 is called the source, or domain (of definition), of the morphism
is called the source, or domain (of definition), of the morphism 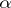 , and
, and 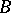 the target, or range (of values), or codomain of
the target, or range (of values), or codomain of 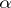 ; instead of
; instead of 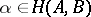 one often writes
one often writes 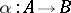 or
or 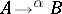 ;
;
2) each morphism of the category 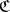 belongs to only one set
belongs to only one set 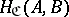 ;
;
3) in the class 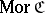 , the following partial composition (product) rule is given: The product of two morphisms
, the following partial composition (product) rule is given: The product of two morphisms 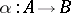 and
and 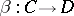 is defined if and only if
is defined if and only if 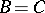 , in which case it belongs to
, in which case it belongs to 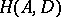 ; the product of
; the product of  and
and 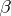 is denoted by
is denoted by 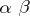 , or, depending on one's choice of conventions, by
, or, depending on one's choice of conventions, by 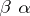 ;
;
4) for any morphisms 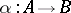 ,
, 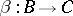 and
and  , the associativity law holds:
, the associativity law holds:
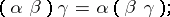 |
5) each set 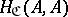 contains a (distinguished) morphism
contains a (distinguished) morphism 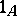 such that
such that  and
and 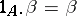 for any morphisms
for any morphisms 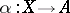 and
and 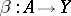 ; the morphisms
; the morphisms 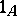 are called units, identities or ones.
are called units, identities or ones.
The notion of a class occurring in the definition of a category presupposes the use of axioms from set theory which distinguish between sets and classes. The most commonly used is the axiom scheme of Gödel–Bernays–von Neumann.
Sometimes, in the definition of a category, it is not required that the classes  be sets. Sometimes, instead of using classes, one assumes the existence of a universal set and requires that the classes
be sets. Sometimes, instead of using classes, one assumes the existence of a universal set and requires that the classes 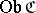 and
and 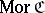 belong to a fixed universal set.
belong to a fixed universal set.
Since there is a bijective correspondence between the identities of a category 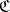 and the class
and the class 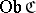 , a category
, a category 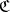 can be defined as a class of morphisms with a partial product satisfying additional conditions (see, for example, [6], [9]).
can be defined as a class of morphisms with a partial product satisfying additional conditions (see, for example, [6], [9]).
The notion of a category was introduced in 1945 [8]. The origins of category theory and the initial stimulus for its development came from algebraic topology. Subsequent investigation revealed the unifying role of the notion of a category and the notion of a functor related to it for many branches of mathematics.
Examples of categories.
1) The category of sets 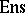 . The class
. The class 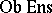 consists of all sets; the class
consists of all sets; the class 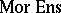 consists of all functions between sets; composition of morphism is composition of functions (see Sets, category of).
consists of all functions between sets; composition of morphism is composition of functions (see Sets, category of).
2) The category of topological spaces 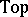 (or
(or 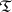 ). The class
). The class 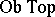 consists of all topological spaces, the class
consists of all topological spaces, the class 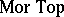 of all continuous mappings, while composition is again composition of mappings.
of all continuous mappings, while composition is again composition of mappings.
3) The category of groups 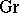 (or
(or 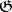 ). The class
). The class 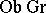 consists of all groups, the class
consists of all groups, the class 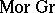 of all group homomorphisms, and composition again is composition of homomorphisms (see Category of groups). One defines in a similar fashion the categories of vector spaces over some field, the category of rings, etc.
of all group homomorphisms, and composition again is composition of homomorphisms (see Category of groups). One defines in a similar fashion the categories of vector spaces over some field, the category of rings, etc.
4) The category of binary relations between sets 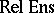 (or
(or 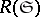 ). The class of objects of this category is
). The class of objects of this category is 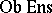 , but as morphisms from
, but as morphisms from  to
to 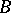 one takes all binary relations, that is, all subsets of the Cartesian product
one takes all binary relations, that is, all subsets of the Cartesian product 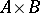 ; composition is composition of binary relations (cf. Binary relation).
; composition is composition of binary relations (cf. Binary relation).
5) A semi-group with identity is a category with a single object; conversely, every category consisting of a single object is a semi-group with identity.
6) A pre-ordered set 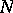 can be regarded as a category
can be regarded as a category 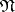 for which
for which 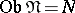 ,
, 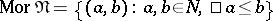 , while the product is defined by the equality
, while the product is defined by the equality 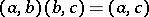 .
.
All categories listed above admit an "isomorphic imbedding" into the category of sets. A category with this property is called a concrete category. Not every category is concrete; for example, the category with as objects all topological spaces and whose morphisms are defined to be homotopy classes of continuous mappings [10].
The number of examples of categories can be considerably enlarged by means of various constructions; foremost, by means of functors of categories or categories of diagrams.
A mapping  between two categories
between two categories 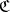 ,
, 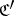 is called a covariant functor (cf. also Functor) if for each object
is called a covariant functor (cf. also Functor) if for each object  ,
, 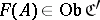 , for each morphism
, for each morphism 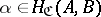 , its image
, its image 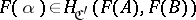 , if
, if 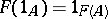 , and if, finally,
, and if, finally, 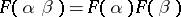 whenever the product
whenever the product 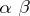 is defined. If the objects of
is defined. If the objects of 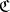 constitute a set, then one can construct the category of diagrams
constitute a set, then one can construct the category of diagrams 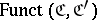 or
or 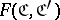 , the objects of which are all covariant functors from
, the objects of which are all covariant functors from 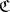 to
to 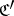 and with as morphisms all natural transformations of these functors.
and with as morphisms all natural transformations of these functors.
To each category  one can associate its dual category
one can associate its dual category 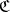 , or
, or 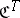 , or
, or 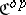 , for which
, for which 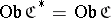 and
and  for any
for any  . A covariant functor from
. A covariant functor from 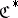 to
to 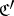 is called a contravariant functor from
is called a contravariant functor from 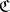 to
to 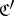 . Along with functors of one argument one can consider many-placed functors or functors of several arguments; cf. Functor.
. Along with functors of one argument one can consider many-placed functors or functors of several arguments; cf. Functor.
For each statement in category theory there is a dual statement, obtained by a formal "reversal of the arrows" . In this connection the so-called duality principle holds: A statement 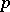 is true in category theory if and only if the dual statement
is true in category theory if and only if the dual statement 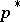 is true.
is true.
Many concepts and results in mathematics turn out to be dual to others from a category-theoretic point of view: injectivity and projectivity, nilpotency and the notion of category of a topological space in the sense of Lyusternik–Shnirel'man, varieties and radicals in algebra, etc.
A category-theoretic analysis of the foundations of homology theory led to the introduction in the mid-fifties of so-called Abelian categories (cf. Abelian category). Within this framework it proved possible to realize the basic constructions of homological algebra [2]. In the 1960s, interest in non-Abelian categories grew, as a result of problems in logic, general algebra, topology, and algebraic geometry. An intensive development of universal algebra and the axiomatic construction of homotopy theory marked the beginnings of various lines of investigation: the category-theoretic study of varieties of universal algebras, the theory of isomorphisms of direct decompositions, the theory of adjoint functors, and the theory of duality of functors. The latter development uncovered the existence of relations between these areas of study. As a result of the recent theory of relative categories, which makes wide use of the techniques of adjoint functors and closed categories, a duality has been established between homotopy theory and the theory of universal algebras; this is based on the interpretation of the categoric definitions of a monoid and a comonoid in suitable categories of functors (see, for example, [7]). Along with the development of the general theory of relative categories special classes of such categories were introduced:  -categories or formal categories; categories with an involution or
-categories or formal categories; categories with an involution or 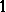 -categories, including, in particular, the category of binary relations; etc. A special case of
-categories, including, in particular, the category of binary relations; etc. A special case of  -categories is the category of small categories, which can be placed at the basis of an axiomatic construction of mathematics.
-categories is the category of small categories, which can be placed at the basis of an axiomatic construction of mathematics.
The classes of categories listed above are characterized by the fact that their sets of morphisms 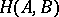 possess an additional structure. Another method of introducing an additional structure in a category is to provide the category with a Grothendieck topology and to construct the category of sheaves over the topologized category (so-called topoi; cf. Topos).
possess an additional structure. Another method of introducing an additional structure in a category is to provide the category with a Grothendieck topology and to construct the category of sheaves over the topologized category (so-called topoi; cf. Topos).
References
| [1] | I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968) |
| [2] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tôhoku Math. J. , 9 (1957) pp. 119–221 |
| [3] | A.G. Kurosh, A.Kh. Livshits, E.G. Shul'geifer, "Foundations of category theory" Uspekhi Mat. Nauk , 15 : 6 (1960) pp. 3–52 (In Russian) |
| [4] | Itogi Nauk. Algebra. Topol. 1962 (1963) pp. 90–106 |
| [5] | Itogi Nauk. Algebra. Topol. Geom. 1967 (1969) pp. 9–57 |
| [6] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
| [7] | M.C. Bunge, "Relative functor categories and categories of algebras" J. of Algebra , 11 (1969) pp. 64–101 |
| [8] | S. Eilenberg, S. MacLane, Trans. Amer. Math. Soc. , 58 (1945) pp. 231–294 |
| [9] | P. Freyd, "Abelian categories: An introduction to the theory of functors" , Harper & Row (1964) |
| [10] | P. Freyd, "On the concreteness of certain categories" , Symp. Math. , 4 , Acad. Press (1970) pp. 431–456 |
| [11] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
| [12] | H. Schubert, "Categories" , 1–2 , Springer (1972) |
| [13] | B. Mitchell, "Theory of categories" , Acad. Press (1965) |
Comments
The notion of a category was introduced in 1942 by S. Eilenberg and S. MacLane [a1], and has since found numerous applications in algebra, topology and the foundations of mathematics. The intuitive idea is that a category consists of all the objects in some "universe of mathematical discourse" together with all the mappings between them. By identifying an object with its identity morphism it is possible to define the notion of a category in terms of morphisms alone. It is intuitively clearer and also more customary to use both objects and morphisms. The two approaches are mixed-up to some extent in the article above. The object and morphism definition is as follows. A category 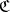 consists of
consists of
A1) a class 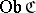 whose elements are called objects of
whose elements are called objects of 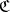 , and a class
, and a class 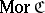 whose elements are called morphisms or arrows of
whose elements are called morphisms or arrows of 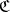 ;
;
A2) operations assigning to each morphism 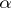 of
of 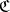 a pair of objects
a pair of objects 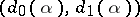 , called the domain and codomain (or source and target) of
, called the domain and codomain (or source and target) of  . One writes "a: A B" or "AaB" to mean "a is a morphism with domain A and codomain B" ; this rephrases 1) above;
. One writes "a: A B" or "AaB" to mean "a is a morphism with domain A and codomain B" ; this rephrases 1) above;
A3) an operation assigning to each object 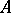 of
of 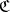 a morphism
a morphism 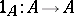 , called the identity morphism on
, called the identity morphism on 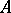 ; this is the precise meaning of part of 5) above;
; this is the precise meaning of part of 5) above;
A4) a partial (binary) product operation for morphisms, the product 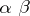 (called the composite of
(called the composite of 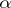 and
and 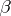 ) being defined if and only if
) being defined if and only if 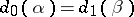 , and satisfying
, and satisfying 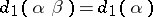 and
and 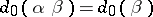 whenever it is defined; this rephrases 3);
whenever it is defined; this rephrases 3);
these data being subject to the axioms
A5) composition is associative, i.e.  whenever both sides are defined; this rephrases 4) above;
whenever both sides are defined; this rephrases 4) above;
A6) identity morphisms are units for composition, i.e. 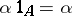 and
and 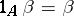 whenever the composites are defined; this and A3) rephrase 5).
whenever the composites are defined; this and A3) rephrase 5).
The classes  and
and 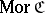 are not required to be sets, and in many of the leading examples (see, e.g. the main text above and the examples (A1)–(A4), (A7) below) they are not sets. However, most examples have the property that, for each pair of objects
are not required to be sets, and in many of the leading examples (see, e.g. the main text above and the examples (A1)–(A4), (A7) below) they are not sets. However, most examples have the property that, for each pair of objects 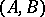 , the collection of morphisms
, the collection of morphisms 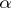 with
with 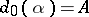 and
and  forms a set (usually denoted by
forms a set (usually denoted by  or
or 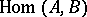 ); such categories are sometimes called locally small, although other writers include this condition as part of the definition of a category. A category
); such categories are sometimes called locally small, although other writers include this condition as part of the definition of a category. A category 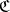 is said to be small if
is said to be small if 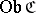 and
and 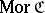 are sets (cf. Small category); it turns out that many of the fundamental mathematical structures may be regarded as small categories (e.g. (A6) and (A7) below).
are sets (cf. Small category); it turns out that many of the fundamental mathematical structures may be regarded as small categories (e.g. (A6) and (A7) below).
It follows from the definition that each object in a category has a unique identity morphism; thus it is possible to identify objects with their identity morphisms, leading to an axiomatization of categories in which "morphism" and "composite" are the only primitive notions (see [9]).
Examples of categories.
(A1) See the main article. The category 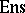 of sets is more often denoted by
of sets is more often denoted by  .
.
(A3) Next to the category  one may consider the categories
one may consider the categories 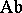 of Abelian groups,
of Abelian groups, 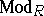 of (right) modules over a fixed ring
of (right) modules over a fixed ring  , etc.
, etc.
(A4) The category of binary relations between sets is usually denoted by 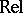 .
.
(A5) A semi-group with identity 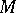 is also called a monoid. It defines a category with one object
is also called a monoid. It defines a category with one object  , the elements of
, the elements of  being interpreted as morphisms
being interpreted as morphisms  .
.
(A6) A partially ordered set 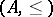 defines a category whose objects are the elements of
defines a category whose objects are the elements of 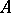 , and whose morphisms are the instances of the order-relation: that is, there is just one morphism
, and whose morphisms are the instances of the order-relation: that is, there is just one morphism 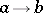 if
if  , and none otherwise.
, and none otherwise.
(A7) Similarly, an oriented graph (or diagram scheme) can be interpreted as a category of which the objects are the vertices and the morphism from 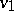 to
to 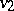 are the oriented paths from
are the oriented paths from 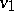 to
to  including the trivial identity paths from
including the trivial identity paths from  to
to  for all vertices. Inversely a category can be seen as a (very large) oriented graph with loops and multiple edges together with an equivalence relation identifying certain paths, cf. [11], Section II.7.
for all vertices. Inversely a category can be seen as a (very large) oriented graph with loops and multiple edges together with an equivalence relation identifying certain paths, cf. [11], Section II.7.
(A8) The homotopy category 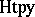 or
or 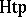 has the same objects as
has the same objects as  , but its morphisms are homotopy classes of continuous mappings. This category can be proved to be nonconcrete.
, but its morphisms are homotopy classes of continuous mappings. This category can be proved to be nonconcrete.
In the study of categories, functors (morphisms of categories) play an essential role. A functor 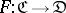 consists of two functions, one assigning to each object
consists of two functions, one assigning to each object 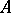 of
of 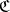 an object
an object 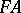 of
of 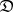 , and the other assigning to each morphism
, and the other assigning to each morphism 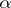 of
of  a morphism
a morphism 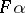 of
of 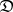 , in such a way that the categorical structure is preserved:
, in such a way that the categorical structure is preserved: 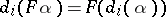
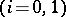 ,
, 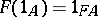 and
and 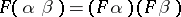 whenever
whenever  is defined. There is also a third level of structure: if
is defined. There is also a third level of structure: if 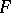 and
and 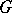 are both functors
are both functors 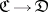 , a natural transformation (or functorial morphism
, a natural transformation (or functorial morphism 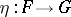 is a function assigning to each object
is a function assigning to each object 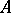 of
of 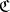 a morphism
a morphism  in
in 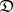 , such that for every
, such that for every 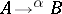 in
in 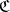 the diagram
the diagram
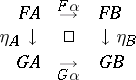 |
commutes (i.e. 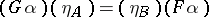 ). Functors may be composed (and every category has an identity functor); thus there is a category
). Functors may be composed (and every category has an identity functor); thus there is a category 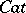 of (small) categories and functors between them. Natural transformations may be composed; thus, given two categories
of (small) categories and functors between them. Natural transformations may be composed; thus, given two categories 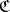 and
and 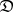 , there is a category
, there is a category 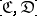 (or
(or 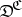 ) of functors
) of functors 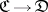 and natural transformations between them. This is one important way in which new categories are constructed from existing ones. The resulting categories are called categories of functors or categories of diagrams. The latter name is especially understandable if
and natural transformations between them. This is one important way in which new categories are constructed from existing ones. The resulting categories are called categories of functors or categories of diagrams. The latter name is especially understandable if 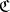 is the category corresponding to a diagram scheme (oriented graph). Indeed, then a functor
is the category corresponding to a diagram scheme (oriented graph). Indeed, then a functor 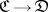 "is" a diagram in
"is" a diagram in 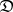 . Other important constructions to obtain new categories are: taking quotients (cf. Quotient category), taking localizations (cf. Localization in categories) and constructing relative and comma categories. The important notion of a derived category involves several of these constructions. If
. Other important constructions to obtain new categories are: taking quotients (cf. Quotient category), taking localizations (cf. Localization in categories) and constructing relative and comma categories. The important notion of a derived category involves several of these constructions. If 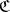 is a category and
is a category and 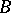 an object of
an object of 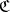 , then the relative category
, then the relative category 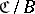 of objects over
of objects over 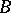 has as objects all morphisms
has as objects all morphisms 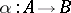 of
of 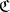 into
into 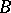 and a morphism in
and a morphism in 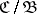 of
of 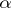 to
to  is a morphism
is a morphism 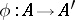 such that
such that 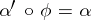 . Dually there is the notion of the relative category of objects in
. Dually there is the notion of the relative category of objects in 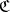 under a given object. Intuitively an object
under a given object. Intuitively an object  of
of 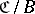 is a family of objects of
is a family of objects of 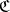 parametrized by
parametrized by 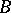 or a fibre object (fibred object). The systematic consideration of these relative objects, i.e. fibre objects (and their duals) combined with base change and deformation ideas has become a most important technique in many parts of mathematics, especially in algebra (notably homological algebra), algebraic and differential geometry, topology, and differential and algebraic topology. It is especially important to find the right fibrewise versions of definitions, theorems and concepts. (A second additional not unrelated major trend involves finding the right equivariant versions in those case in which there is a group of symmetries present (as well).)
or a fibre object (fibred object). The systematic consideration of these relative objects, i.e. fibre objects (and their duals) combined with base change and deformation ideas has become a most important technique in many parts of mathematics, especially in algebra (notably homological algebra), algebraic and differential geometry, topology, and differential and algebraic topology. It is especially important to find the right fibrewise versions of definitions, theorems and concepts. (A second additional not unrelated major trend involves finding the right equivariant versions in those case in which there is a group of symmetries present (as well).)
The idea of a comma category generalizes that of categories of objects over or under a given object. Let there be given three categories 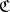 ,
, 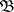 ,
, 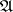 and two functors
and two functors 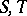 arranged as follows
arranged as follows
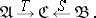 |
Then the comma category 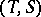 or
or 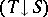 has as objects all triples
has as objects all triples 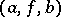 consisting of an object
consisting of an object 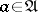 , an object
, an object 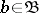 and a morphism
and a morphism  in
in 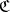 . A morphism
. A morphism  from
from 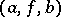 to
to  consists of a pair of morphisms
consists of a pair of morphisms 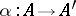 and
and 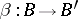 such that
such that 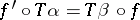 .
.
Examples of functors. ITEM {(A9} The forgetful functor 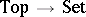 sends each topological space to its underlying set, and each continuous function to itself ( "forgetting" the continuity). Similarly, one has forgetful functors
sends each topological space to its underlying set, and each continuous function to itself ( "forgetting" the continuity). Similarly, one has forgetful functors  ,
, 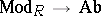 , etc.
, etc.
(A10) If 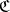 is a locally small category, then for each
is a locally small category, then for each 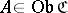 there is a functor
there is a functor 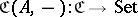 sending
sending 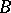 to the set
to the set 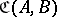 and
and 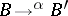 to the function which sends
to the function which sends 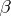 to
to 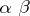 . Such functors (or functors isomorphic to them in
. Such functors (or functors isomorphic to them in 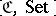 ) are called representable (cf. Representable functor).
) are called representable (cf. Representable functor).
(A11) There is a functor  sending a set
sending a set  to the free group generated by
to the free group generated by 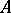 , and a function
, and a function 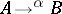 to the unique homomorphism
to the unique homomorphism 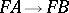 sending the generator
sending the generator  of
of 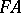 to
to 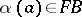 , for each
, for each 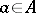 .
.
(A12) The (singular) homology groups of spaces (cf. Homology group) define functors 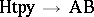 (one for each dimension
(one for each dimension  ).
).
(A13) A functor between monoids, considered as categories, is just a monoid homomorphism.
(A14) A functor between partially ordered sets, considered as categories, is just an order-preserving mapping.
(A15) If 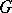 is a group, considered as a category, a functor
is a group, considered as a category, a functor 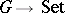 (respectively,
(respectively, 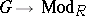 ) is a permutation (respectively, an
) is a permutation (respectively, an 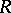 -linear representation) of
-linear representation) of 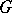 (cf. Representation of a group).
(cf. Representation of a group).
A functor 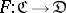 is said to be faithful (cf. Faithful functor) if it is "injective on Hom-sets" ; i.e. if, given two morphisms
is said to be faithful (cf. Faithful functor) if it is "injective on Hom-sets" ; i.e. if, given two morphisms 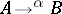 and
and  with the same domain and codomain in
with the same domain and codomain in 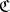 ,
, 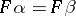 implies
implies 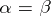 .
. 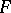 is said to be full if it is "surjective on Hom-sets" in a similar sense. Forgetful functors (as in (A9) above) are always faithful. The property that a category
is said to be full if it is "surjective on Hom-sets" in a similar sense. Forgetful functors (as in (A9) above) are always faithful. The property that a category 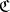 be concrete can now be rephrased as: There is a faithful functor
be concrete can now be rephrased as: There is a faithful functor 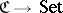 .
.
Given a category 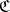 , one can form its opposite or dual category
, one can form its opposite or dual category 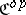 by keeping the same objects as
by keeping the same objects as 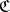 and reversing all the morphisms. The category
and reversing all the morphisms. The category 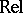 is isomorphic to its opposite, though most familiar categories are not. A functor
is isomorphic to its opposite, though most familiar categories are not. A functor 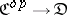 is sometimes called a contravariant functor from
is sometimes called a contravariant functor from 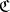 to
to 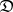 ; for emphasis, functors
; for emphasis, functors 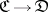 are then called covariant. (For example, if
are then called covariant. (For example, if  is locally small, one may define a contravariant functor
is locally small, one may define a contravariant functor 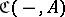 from
from 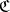 to
to 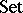 , by analogy with the covariant functor
, by analogy with the covariant functor 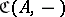 of example (A10) above.) The duality principle for categories is essentially the assertion that something which is true for all categories is true for the duals of all categories.
of example (A10) above.) The duality principle for categories is essentially the assertion that something which is true for all categories is true for the duals of all categories.
S. MacLane [a4] introduced the idea that Cartesian products can be characterized in categorical terms, by a universal property; this gave rise to the general categorical notion of limit (and the dual notion of colimit), which includes products as a special case (cf. Limit and Universal problems).
The key notion of adjunction came latter [a5]: given functors 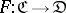 and
and 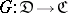 , one says that
, one says that 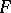 is left adjoint to
is left adjoint to 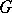 (written
(written 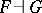 ) if there is a bijection between morphisms
) if there is a bijection between morphisms  and morphisms
and morphisms 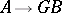 which is natural in
which is natural in 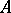 and
and 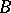 ; this is equivalent to the existence of natural transformations
; this is equivalent to the existence of natural transformations 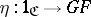 and
and 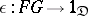 satisfying certain identities [11] (cf. Adjoint functor). For example, the free group functor (example (A11) above) is left adjoint to the forgetful functor
satisfying certain identities [11] (cf. Adjoint functor). For example, the free group functor (example (A11) above) is left adjoint to the forgetful functor 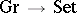 ; Galois connections (cf. Galois correspondence) are examples of (contravariant) adjunctions between partially ordered sets. A functor which has a left adjoint preserves all limits; the converse implication is valid under suitable "smallness conditions" (the adjoint functor theorem, see [9]).
; Galois connections (cf. Galois correspondence) are examples of (contravariant) adjunctions between partially ordered sets. A functor which has a left adjoint preserves all limits; the converse implication is valid under suitable "smallness conditions" (the adjoint functor theorem, see [9]).
Given an adjunction 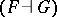 as above, the composite functor
as above, the composite functor 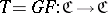 is equipped with natural transformations
is equipped with natural transformations 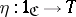 and
and 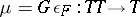 satisfying certain identities; these data define the notion of a monad or triple on a category, which played a central role in much categorical research in the 1960's and later years.
satisfying certain identities; these data define the notion of a monad or triple on a category, which played a central role in much categorical research in the 1960's and later years.
The identities which a triple 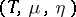 on a category
on a category 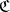 is required to satisfy are the following:
is required to satisfy are the following: 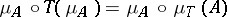 ,
, 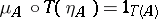 ,
, 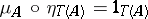 . An algebra for the triple
. An algebra for the triple 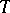 , or
, or 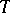 -algebra, is an object
-algebra, is an object 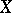 of
of 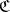 together with a morphism
together with a morphism 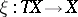 such that the following identities hold:
such that the following identities hold: 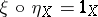 ,
, 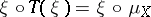 . It is a good idea to write out these requirements in terms of commutative diagrams. They are reminiscent of associativity and unit requirements.
. It is a good idea to write out these requirements in terms of commutative diagrams. They are reminiscent of associativity and unit requirements.
Dually, i.e. reversing all arrows, there is the notion of a cotriple and the corresponding notion of a co-algebra over such a cotriple. An important example of a cotriple in the category  of commutative rings with unit element is the functor
of commutative rings with unit element is the functor  of the big Witt vectors together with the structure of a special
of the big Witt vectors together with the structure of a special 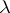 -ring on
-ring on 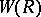 . The co-algebras for this cotriple are precisely the special
. The co-algebras for this cotriple are precisely the special 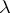 -algebras (cf. Witt vector and
-algebras (cf. Witt vector and 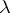 -ring).
-ring).
Important examples of triples arise from adjunctions involving forgetful functors. For example, let 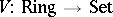 be the forgetful functor from the category of commutative rings with unit element to the category of sets. This one has an adjoint
be the forgetful functor from the category of commutative rings with unit element to the category of sets. This one has an adjoint 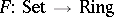 which assigns to a set
which assigns to a set 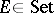 the free commutative ring with generator
the free commutative ring with generator 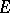 , i.e. the ring
, i.e. the ring 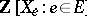 of commutative polynomials over
of commutative polynomials over 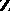 in the variables
in the variables 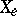 ,
, 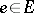 . The freeness property of
. The freeness property of 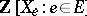 , i.e. the property that for every ring
, i.e. the property that for every ring 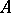 and every collection of elements
and every collection of elements 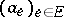 of
of 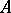 there is precisely one homomorphism of rings
there is precisely one homomorphism of rings  such that
such that 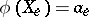 for all
for all 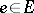 , precisely expresses the fact that
, precisely expresses the fact that 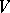 and
and 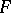 are adjoint functors:
are adjoint functors: 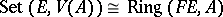 . The corresponding natural transformation
. The corresponding natural transformation 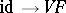 is given by
is given by 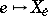 (cf. also Adjoint functor).
(cf. also Adjoint functor).
Every monad and comonad can be induced by an adjunction; in fact there is a "best possible" such adjunction, in which 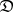 is taken to be the category of (Eilenberg–Moore) algebras for the monad, [a7]. A general adjunction
is taken to be the category of (Eilenberg–Moore) algebras for the monad, [a7]. A general adjunction 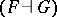 is said to be monadic (or
is said to be monadic (or 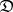 is said to be monadic over
is said to be monadic over 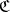 ) if
) if 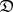 is (canonically) equivalent to the category of algebras for the induced monad on
is (canonically) equivalent to the category of algebras for the induced monad on 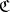 . The adjunction between the
. The adjunction between the 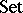 and
and 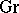 , mentioned above, is monadic; more generally, the categories which are monadic over
, mentioned above, is monadic; more generally, the categories which are monadic over 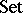 can be characterized [a8] as those which arise from varieties of universal algebras (provided one allows infinitary as well as finitary algebraic operations; the finitary case can also be characterized in categorical terms [9], using the notion of algebraic theory). See also Variety of universal algebras.
can be characterized [a8] as those which arise from varieties of universal algebras (provided one allows infinitary as well as finitary algebraic operations; the finitary case can also be characterized in categorical terms [9], using the notion of algebraic theory). See also Variety of universal algebras.
Another phrase that is used to denote a triple 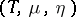 is algebraic theory (in monad form) over the category
is algebraic theory (in monad form) over the category 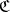 . It is so to speak the theory of the category of
. It is so to speak the theory of the category of 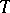 -algebras. There are, at least, two more equivalent ways in which this notion is approached. One is as follows [a6]. An algebraic theory in clone form
-algebras. There are, at least, two more equivalent ways in which this notion is approached. One is as follows [a6]. An algebraic theory in clone form 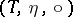 consists of an "object assignment function"
consists of an "object assignment function" 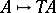 (
(
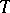 -terms with variables in
-terms with variables in 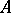 ) for all objects
) for all objects 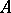 , an "insertion of variables mapping"
, an "insertion of variables mapping" 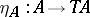 for all
for all 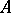 and a "clone-composition function"
and a "clone-composition function" 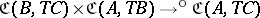 for each ordered triple
for each ordered triple  of objects of
of objects of  . For each
. For each 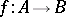 in
in 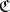 let
let 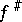 be the composite
be the composite 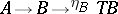 . Then the data
. Then the data 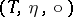 are supposed to satisfy the following axioms. For all
are supposed to satisfy the following axioms. For all 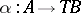 ,
, 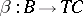 ,
, 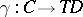 and
and 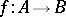 ,
,
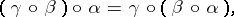 |
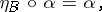 |
 |
This defines a new category 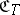 , the Kleishi category of
, the Kleishi category of 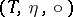 . The objects of
. The objects of 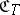 are the objects of
are the objects of 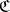 ,
,  , composition is given by
, composition is given by  , and the identity morphisms are the
, and the identity morphisms are the 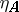 in
in 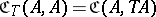 .
.
A simple example of an algebraic theory in clone form is as follows. Let 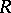 be a ring with unit. For a set
be a ring with unit. For a set 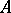 let
let 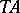 be the vector space
be the vector space  . A matrix with columns indexed by
. A matrix with columns indexed by 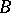 and rows indexed by
and rows indexed by  is a mapping
is a mapping 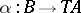 , i.e. a morphism in
, i.e. a morphism in 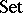 ;
; 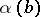 is the
is the 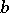 -th column of the matrix. Given an
-th column of the matrix. Given an 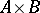 matrix
matrix 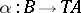 and a
and a 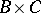 matrix
matrix  , define their composite
, define their composite 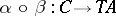 by the usual matrix product, i.e.
by the usual matrix product, i.e. 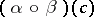 is the
is the 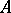 -vector with components
-vector with components
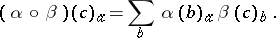 |
The insertion of variables assignment  is defined by
is defined by  where
where 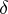 denotes the Kronecker delta (cf. Kronecker symbol). It is easily checked that the axioms above are satisfied.
denotes the Kronecker delta (cf. Kronecker symbol). It is easily checked that the axioms above are satisfied.
Let 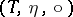 be an algebraic theory in clone form. For
be an algebraic theory in clone form. For 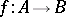 in
in 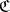 define
define 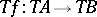 as the composite
as the composite 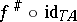 . It follows readily that
. It follows readily that 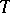 is then a functor and that
is then a functor and that 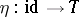 is a natural transformation. Further define
is a natural transformation. Further define 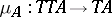 as the composite
as the composite 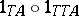 . Then
. Then 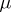 is also a natural transformation and
is also a natural transformation and 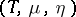 is a triple. Moreover, this construction yielding a triple for each algebraic theory in clone form is a bijection. For a discussion of the algebraic theories (in clone and monad form) coming from a universal algebra and a third categorical way of viewing universal algebras see Universal algebra.
is a triple. Moreover, this construction yielding a triple for each algebraic theory in clone form is a bijection. For a discussion of the algebraic theories (in clone and monad form) coming from a universal algebra and a third categorical way of viewing universal algebras see Universal algebra.
The language of categories and functors was originally introduced to meet the needs of algebraic topology and homological algebra [a1], [a4]. In the 1950's and early 1960's much attention was focused on Abelian categories (cf. Abelian category), which may be defined as categories satisfying all the elementary properties of 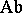 ; it was shown in [2] that they provide an adequate foundation for the development of homological algebra, and in [a11] that every small Abelian category admits a full imbedding, preserving finite limits and colimits, into
; it was shown in [2] that they provide an adequate foundation for the development of homological algebra, and in [a11] that every small Abelian category admits a full imbedding, preserving finite limits and colimits, into 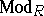 for some
for some  .
.
In an Abelian category 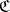 , the "Hom-sets"
, the "Hom-sets" 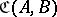 have a natural Abelian group structure; this observation provided one of the incentives for developing the theory of enriched (or relative) categories [a12], that is, categories whose "Hom-sets" are objects of some "base category"
have a natural Abelian group structure; this observation provided one of the incentives for developing the theory of enriched (or relative) categories [a12], that is, categories whose "Hom-sets" are objects of some "base category" 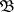 . Categories enriched over themselves (such as
. Categories enriched over themselves (such as  and
and 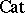 ) are called closed categories [a13] (cf. Closed category); an important class of closed categories (including
) are called closed categories [a13] (cf. Closed category); an important class of closed categories (including 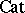 but not
but not 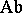 ) consists of those where the closed structure (the "internal Hom" ) is related by an adjunction to the categorical product structure — such categories are called Cartesian closed. The notion of a Cartesian closed category played an important role in F.W. Lawvere's axiomatization of the category of small categories as a foundation for mathematics [a14], and in his latter development with M. Tierney of the notion of an elementary topos, which has dominated much of categorical research in the 1970's and 1980's (see [a15]). Cartesian closed categories are also of importance in logic, since they provide models for the (typed)
) consists of those where the closed structure (the "internal Hom" ) is related by an adjunction to the categorical product structure — such categories are called Cartesian closed. The notion of a Cartesian closed category played an important role in F.W. Lawvere's axiomatization of the category of small categories as a foundation for mathematics [a14], and in his latter development with M. Tierney of the notion of an elementary topos, which has dominated much of categorical research in the 1970's and 1980's (see [a15]). Cartesian closed categories are also of importance in logic, since they provide models for the (typed) 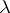 -calculus (see [a16]).
-calculus (see [a16]).
Categories enriched over 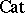 (commonly called
(commonly called  -categories) have also received a good deal of attention in recent years. They are distinguished from the general run of enriched categories by the possibility of considering diagrams within them which commute "up to isomorphism" but not exactly; the weaker notion of a bicategory [a17] is a further expression of this idea.
-categories) have also received a good deal of attention in recent years. They are distinguished from the general run of enriched categories by the possibility of considering diagrams within them which commute "up to isomorphism" but not exactly; the weaker notion of a bicategory [a17] is a further expression of this idea.  -categories and higher-dimensional categories have also been studied, and have proved to be of importance in the algebraic study of homotopy types [a18]. In these areas of category theory coherence theorems play an important part: these are theorems which allow one to deduce the commutativity of a large class of diagrams from that of certain particular diagrams (see [a19], for example).
-categories and higher-dimensional categories have also been studied, and have proved to be of importance in the algebraic study of homotopy types [a18]. In these areas of category theory coherence theorems play an important part: these are theorems which allow one to deduce the commutativity of a large class of diagrams from that of certain particular diagrams (see [a19], for example).
Further areas of category theory in which much work has been done in recent years include the theory of fibred categories [a2] (which, together with enriched category theory, is an expression of the idea that 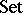 can be replaced by some more general base category as a foundation for much of mathematics), and the theory of topological categories [a3] (which is concerned with the study of concrete categories whose forgetful functors to
can be replaced by some more general base category as a foundation for much of mathematics), and the theory of topological categories [a3] (which is concerned with the study of concrete categories whose forgetful functors to 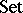 have good infinitary properties, similar to those of the forgetful functor
have good infinitary properties, similar to those of the forgetful functor 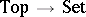 , see also Topologized category).
, see also Topologized category).
In addition to the books [9] and [11], [12] and [13] may also be recommended as general accounts of category theory.
References
| [a1] | S. Eilenberg, S. MacLane, "Natural isomorphisms in group theory" Proc. Nat. Sci. USA , 28 (1942) pp. 537–543 |
| [a2] | J. Bénabou, "Fibred categories and the foundations of naive category theory" J. Symbolic Logic , 50 (1985) pp. 10–37 |
| [a3] | G.C.L. Brümmer, "Topological categories" Topology Appl. , 18 (1984) pp. 27–41 |
| [a4] | S. MacLane, "Duality for groups" Bull. Amer. Math. Soc. , 56 (1950) pp. 485–516 |
| [a5] | D.M. Kan, "Adjoint functors" Trans. Amer. Math. Soc. , 87 (1958) pp. 294–329 |
| [a6] | E.G. Manes, "Algebraic theories" , Springer (1976) |
| [a7] | S. Eilenberg, J.C. Moore, "Adjoint functors and triples" Ill. J. Math. , 9 (1965) pp. 381–398 |
| [a8] | F.E.J. Linton, "Some aspects of equational categories" S. Eilenberg (ed.) et al. (ed.) , Proc. conf. categorical algebra (La Jolla, 1965) , Springer (1966) pp. 84–94 |
| [a9] | F.W. Lawvere, "Functorial semantics of algebraic theories" Proc. Nat. Acad. Sci. USA , 50 (1963) pp. 869–872 |
| [a10] | B. Pareigis, "Categories and functors" , Acad. Press (1970) |
| [a11] | B. Mitchell, "The full imbedding theorem" Amer. J. Math. , 86 (1964) pp. 619–637 |
| [a12] | G.M. Kelly, "Basic concepts of enriched category theory" , Cambridge Univ. Press (1982) |
| [a13] | G.M. Kelly, "Closed categories" S. Eilenberg (ed.) et al. (ed.) , Proc. conf. categorical algebra (La Jolla, 1965) , Springer (1966) pp. 421–562 |
| [a14] | F.W. Lawvere, "The category of categories as a foundation for mathematics" S. Eilenberg (ed.) et al. (ed.) , Proc. conf. categorical algebra (La Jolla, 1965) , Springer (1966) pp. 1–20 |
| [a15] | P.T. Johnstone, "Topos theory" , Acad. Press (1977) |
| [a16] | J. Lambek, P.J. Scott, "Introduction to higher-order categorical logic" , Cambridge Univ. Press (1986) |
| [a17] | J. Bénabou, "Introduction to bicategories" , Reports of the Midwest Category Seminar I , Lect. notes in math. , 47 , Springer (1967) pp. 1–77 |
| [a18] | R. Brown, P.J. Higgins, "The equivalence of  -groupoids and crossed complexes" Cahiers Top. et Géom. Diff. , 22 (1981) pp. 371–386 -groupoids and crossed complexes" Cahiers Top. et Géom. Diff. , 22 (1981) pp. 371–386 |
| [a19] | S. MacLane, "Why commutative diagrams coincide with equivalent proofs" , Algebraists' Homage , Contemp. Math. , 13 , Amer. Math. Soc. (1982) pp. 387–401 |
Category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Category&oldid=19164