Buchsbaum ring
The notion of a Buchsbaum ring (and module) is a generalization of that of a Cohen–Macaulay ring (respectively, module). Let 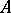 denote a Noetherian local ring (cf. also Noetherian ring) with maximal ideal
denote a Noetherian local ring (cf. also Noetherian ring) with maximal ideal 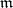 and
and  . Let
. Let 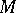 be a finitely-generated
be a finitely-generated  -module with
-module with 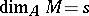 . Then
. Then 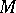 is called a Buchsbaum module if the difference
is called a Buchsbaum module if the difference
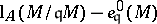 |
is independent of the choice of a parameter ideal 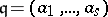 of
of 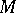 , where
, where  is a system of parameters of
is a system of parameters of 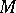 and
and 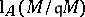 (respectively,
(respectively, 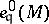 ) denotes the length of the
) denotes the length of the 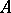 -module
-module  (respectively, the multiplicity of
(respectively, the multiplicity of 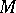 with respect to
with respect to 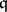 ). When this is the case, the difference
). When this is the case, the difference
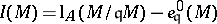 |
is called the Buchsbaum invariant of 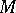 . The
. The 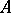 -module
-module 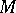 is a Cohen–Macaulay module if and only if
is a Cohen–Macaulay module if and only if 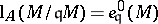 for some (and hence for any) parameter ideal
for some (and hence for any) parameter ideal 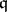 of
of 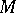 , so that
, so that 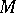 is a Cohen–Macaulay
is a Cohen–Macaulay 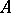 -module if and only if
-module if and only if 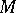 is a Buchsbaum
is a Buchsbaum 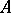 -module with
-module with 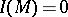 . The ring
. The ring 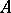 is said to be a Buchsbaum ring if
is said to be a Buchsbaum ring if 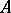 is a Buchsbaum module over itself. If
is a Buchsbaum module over itself. If 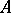 is a Buchsbaum ring, then
is a Buchsbaum ring, then 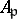 is a Cohen–Macaulay ring with
is a Cohen–Macaulay ring with 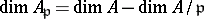 for every
for every 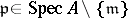 .
.
A typical example of Buchsbaum rings is as follows. Let
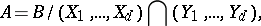 |
where 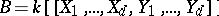 , with
, with 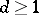 , denotes the formal power series ring in
, denotes the formal power series ring in 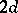 variables over a field
variables over a field 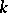 . Then
. Then 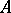 is a Buchsbaum ring with
is a Buchsbaum ring with 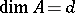 and
and 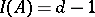 .
.
A, not necessarily local, Noetherian ring 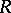 is said to be a Buchsbaum ring if the local rings
is said to be a Buchsbaum ring if the local rings 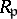 are Buchsbaum for all
are Buchsbaum for all 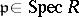 .
.
The theory of Buchsbaum rings and modules dates back to a question raised in 1965 by D.A. Buchsbaum [a3]. He asked whether the difference 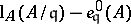 , with
, with 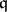 a parameter ideal, is an invariant for any Noetherian local ring
a parameter ideal, is an invariant for any Noetherian local ring 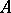 . This is, however, not the case and a counterexample was given in [a28]. Thereafter, in 1973 J. Stückrad and W. Vogel published the classic paper [a29], from which the history of Buchsbaum rings and modules started. In [a29] they gave a characterization of Buchsbaum rings in terms of the following property of systems of parameters: A
. This is, however, not the case and a counterexample was given in [a28]. Thereafter, in 1973 J. Stückrad and W. Vogel published the classic paper [a29], from which the history of Buchsbaum rings and modules started. In [a29] they gave a characterization of Buchsbaum rings in terms of the following property of systems of parameters: A 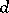 -dimensional Noetherian local ring
-dimensional Noetherian local ring 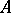 with maximal ideal
with maximal ideal 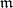 is Buchsbaum if and only if every system
is Buchsbaum if and only if every system  of parameters for
of parameters for 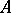 forms a weak
forms a weak 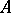 -sequence, that is, the equality
-sequence, that is, the equality
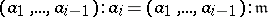 |
holds for all 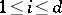 . Therefore, systems
. Therefore, systems  of parameters in a Buchsbaum local ring need not be regular sequences, but the differences
of parameters in a Buchsbaum local ring need not be regular sequences, but the differences
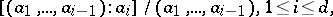 |
are very small and only finite-dimensional vector spaces over the residue class field 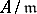 of
of 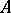 . Weak sequences are closely related to
. Weak sequences are closely related to 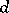 -sequences introduced by C. Huneke [a21]. Actually,
-sequences introduced by C. Huneke [a21]. Actually, 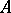 is a Buchsbaum ring if and only if every system
is a Buchsbaum ring if and only if every system  of parameters for
of parameters for 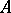 forms a
forms a 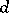 -sequence, that is, the equality
-sequence, that is, the equality
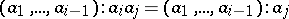 |
holds for all 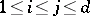 .
.
One of the fundamental results on Buchsbaum rings and modules is the surjectivity criterion. Let
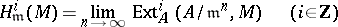 |
denote the 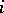 th local cohomology of
th local cohomology of 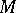 with respect to the maximal ideal
with respect to the maximal ideal 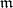 . If
. If 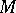 is a Buchsbaum
is a Buchsbaum 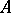 -module, then
-module, then 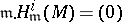 for all
for all 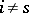 and the equality
and the equality
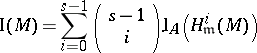 |
holds, where 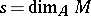 .
.
Unfortunately, the vanishing does not characterize Buchsbaum modules. Modules  with
with 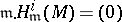 for all
for all 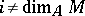 are called quasi-Buchsbaum and constitute a class which is strictly larger than that of Buchsbaum modules. However, if the canonical homomorphism
are called quasi-Buchsbaum and constitute a class which is strictly larger than that of Buchsbaum modules. However, if the canonical homomorphism
 |
is surjective for all 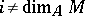 , then
, then 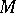 is a Buchsbaum
is a Buchsbaum 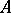 -module. The converse is also true if the base ring
-module. The converse is also true if the base ring 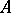 is regular (cf. also Regular ring (in commutative algebra)).
is regular (cf. also Regular ring (in commutative algebra)).
After the establishment of the surjectivity criterion, by Stückrad and Vogel [a30] in 1978, the development of the theory became rather rapid. The ubiquity of Buchsbaum normal local rings was established by S. Goto [a6] as an application of the Evans–Griffith construction [a5]. Namely, let 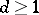 and
and 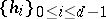 be integers. Then there exists a Buchsbaum local ring
be integers. Then there exists a Buchsbaum local ring 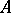 with
with 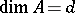 and
and 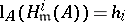 for
for 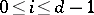 . If
. If 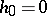 (respectively,
(respectively, 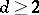 and
and 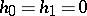 ), one may choose the ring
), one may choose the ring 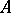 so that
so that  is an integral domain (respectively, a normal ring). See [a1] for progress in the research about the ubiquity of Buchsbaum homogeneous integral domains. Besides, Buchsbaum local rings of multiplicity
is an integral domain (respectively, a normal ring). See [a1] for progress in the research about the ubiquity of Buchsbaum homogeneous integral domains. Besides, Buchsbaum local rings of multiplicity  have been classified [a8]. Also, certain famous isolated singularities are Buchsbaum (cf. [a23]).
have been classified [a8]. Also, certain famous isolated singularities are Buchsbaum (cf. [a23]).
The theory of Buchsbaum rings and modules is closely related to that of Cohen–Macaulayness in blowing-ups. Let 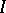 be an ideal of positive height in a Noetherian local ring
be an ideal of positive height in a Noetherian local ring 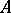 . Let
. Let 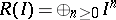 and call it the Rees algebra of
and call it the Rees algebra of 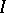 . Then the canonical morphism
. Then the canonical morphism 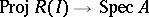 is the blowing-up of
is the blowing-up of 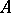 with centre
with centre 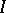 (cf. also Blow-up algebra). If the ring
(cf. also Blow-up algebra). If the ring 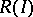 is Cohen–Macaulay, then the scheme
is Cohen–Macaulay, then the scheme 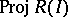 naturally is locally Cohen–Macaulay. The problem when the Rees algebra
naturally is locally Cohen–Macaulay. The problem when the Rees algebra 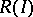 is Cohen–Macaulay has been intensively studied from the 1980s onwards ([a18], [a38], [a16], [a39], [a17]).
is Cohen–Macaulay has been intensively studied from the 1980s onwards ([a18], [a38], [a16], [a39], [a17]).
The ring 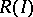 is Cohen–Macaulay if the ideal
is Cohen–Macaulay if the ideal 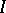 is generated by a regular sequence and if the base ring
is generated by a regular sequence and if the base ring 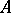 is Cohen–Macaulay [a2]. However, the converse is not true even for parameter ideals
is Cohen–Macaulay [a2]. However, the converse is not true even for parameter ideals 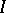 . Actually,
. Actually, 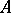 is a Buchsbaum ring if and only if the Rees algebra
is a Buchsbaum ring if and only if the Rees algebra 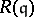 is a Cohen–Macaulay ring for every parameter ideal
is a Cohen–Macaulay ring for every parameter ideal 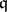 in
in 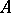 , provided that
, provided that 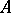 is an integral domain with
is an integral domain with 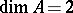 . This insightful result of Y. Shimoda [a35] in 1979 opened the door towards a further development of the theory. Firstly, Goto and Shimoda [a19] showed that a Noetherian local ring
. This insightful result of Y. Shimoda [a35] in 1979 opened the door towards a further development of the theory. Firstly, Goto and Shimoda [a19] showed that a Noetherian local ring 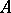 is a Buchsbaum ring with
is a Buchsbaum ring with 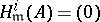 (
(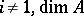 ) if and only if the Rees algebra
) if and only if the Rees algebra 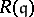 is a Cohen–Macaulay ring for every parameter ideal
is a Cohen–Macaulay ring for every parameter ideal 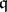 in
in 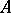 . When this is the case, the Rees algebras
. When this is the case, the Rees algebras 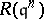 are also Cohen–Macaulay for all
are also Cohen–Macaulay for all 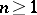 . In 1981, Buchsbaum rings were characterized in terms of the blowing-ups of parameter ideals. Let
. In 1981, Buchsbaum rings were characterized in terms of the blowing-ups of parameter ideals. Let 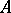 be a Noetherian local ring with maximal ideal
be a Noetherian local ring with maximal ideal 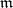 and
and 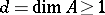 . Then
. Then 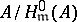 is a Buchsbaum ring if and only if the scheme
is a Buchsbaum ring if and only if the scheme 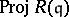 is locally Cohen–Macaulay for every parameter ideal
is locally Cohen–Macaulay for every parameter ideal 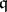 in
in 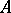 [a7]. Subsequently, Goto [a10] proved that the associated graded rings
[a7]. Subsequently, Goto [a10] proved that the associated graded rings 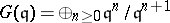 of parameter ideals
of parameter ideals 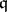 in a Buchsbaum local ring are always Buchsbaum. In addition, Stückrad showed that
in a Buchsbaum local ring are always Buchsbaum. In addition, Stückrad showed that 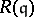 is a Buchsbaum ring for every parameter ideal
is a Buchsbaum ring for every parameter ideal 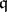 in a Buchsbaum local ring [a36]. The systems of parameters in Buchsbaum local rings behave very well and enjoy the monomial property [a10].
in a Buchsbaum local ring [a36]. The systems of parameters in Buchsbaum local rings behave very well and enjoy the monomial property [a10].
Buchsbaum rings are yet (2000) the only non-trivial case for which the monomial conjecture, raised by M. Hochster, has been solved affirmatively (except for the equi-characteristic case). See [a31] for these results, together with geometric applications and concrete examples. See [a31] for researches on the Buchsbaum property in affine semi-group rings and Stanley–Reisner rings of simplicial complexes.
Let 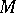 be a Buchsbaum module over a Noetherian local ring
be a Buchsbaum module over a Noetherian local ring 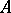 . Then
. Then 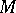 is said to be maximal if
is said to be maximal if 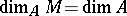 . Noetherian local rings possessing only finitely many isomorphism classes of indecomposable maximal Buchsbaum modules are said to have finite Buchsbaum-representation type. Buchsbaum representation theory was studied by Goto and K. Nishida [a15], [a11], [a13], and the Cohen–Macaulay local rings
. Noetherian local rings possessing only finitely many isomorphism classes of indecomposable maximal Buchsbaum modules are said to have finite Buchsbaum-representation type. Buchsbaum representation theory was studied by Goto and K. Nishida [a15], [a11], [a13], and the Cohen–Macaulay local rings 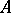 of finite Buchsbaum-representation type have been classified under certain mild conditions. If
of finite Buchsbaum-representation type have been classified under certain mild conditions. If 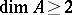 , then
, then 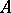 must be regular [a15]. The situation is a little more complicated if
must be regular [a15]. The situation is a little more complicated if 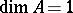 [a13]. In [a11] (not necessarily Cohen–Macaulay) surface singularities of finite Buchsbaum-representation type are classified.
[a13]. In [a11] (not necessarily Cohen–Macaulay) surface singularities of finite Buchsbaum-representation type are classified.
Suppose that 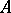 is a regular local ring with
is a regular local ring with 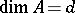 and let
and let  be a maximal Buchsbaum
be a maximal Buchsbaum 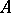 -module. Then
-module. Then 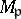 is a free
is a free 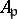 -module for all
-module for all 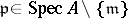 , so that the
, so that the 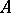 -module
-module 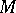 defines a vector bundle on the punctured spectrum
defines a vector bundle on the punctured spectrum 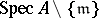 of
of 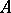 . Thanks to the surjectivity criterion, one can prove the structure theorem of maximal Buchsbaum modules over regular local rings: Every maximal Buchsbaum
. Thanks to the surjectivity criterion, one can prove the structure theorem of maximal Buchsbaum modules over regular local rings: Every maximal Buchsbaum 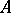 -module
-module 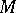 has the form
has the form
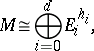 |
where 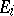 denotes the
denotes the 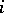 th syzygy module of the residue class field
th syzygy module of the residue class field 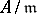 of
of 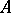 ,
, 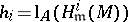 (
(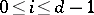 ), and
), and 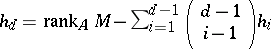 , if
, if 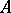 is a regular local ring ([a4], [a12]). This result has been generalized by Y. Yoshino [a40] and T. Kawasaki [a24]. They showed a similar decomposition theorem of a special kind of maximal Buchsbaum modules over Gorenstein local rings; see [a32] for the characterization of Buchsbaum rings and modules in terms of dualizing complexes. (It should be noted here that the main result in [a32] contains a serious mistake, which has been repaired in [a40].)
is a regular local ring ([a4], [a12]). This result has been generalized by Y. Yoshino [a40] and T. Kawasaki [a24]. They showed a similar decomposition theorem of a special kind of maximal Buchsbaum modules over Gorenstein local rings; see [a32] for the characterization of Buchsbaum rings and modules in terms of dualizing complexes. (It should be noted here that the main result in [a32] contains a serious mistake, which has been repaired in [a40].)
A local ring 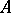 satisfying the condition that all the local cohomology modules
satisfying the condition that all the local cohomology modules  (
( ) are finitely generated is said to be an FLC ring (or a generalized Cohen–Macaulay ring). The class of FLC rings includes Buchsbaum rings as typical examples. In fact, a Noetherian local ring
) are finitely generated is said to be an FLC ring (or a generalized Cohen–Macaulay ring). The class of FLC rings includes Buchsbaum rings as typical examples. In fact, a Noetherian local ring 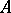 is FLC if and only if it contains at least one system
is FLC if and only if it contains at least one system  (
(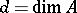 ) of parameters such that the sequence
) of parameters such that the sequence 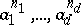 forms a
forms a 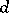 -sequence in any order for all integers
-sequence in any order for all integers 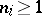 . Such a sequence is called an unconditioned strong
. Such a sequence is called an unconditioned strong 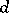 -sequence (for short, USD-sequence or
-sequence (for short, USD-sequence or 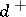 -sequence); they have been intensively studied [a27], [a37], [a20]. Recently (1999), Kawasaki [a25] used the results in [a20] to establish the arithmetic Cohen–Macaulayfications of Noetherian local rings. Namely, every unmixed local ring
-sequence); they have been intensively studied [a27], [a37], [a20]. Recently (1999), Kawasaki [a25] used the results in [a20] to establish the arithmetic Cohen–Macaulayfications of Noetherian local rings. Namely, every unmixed local ring 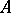 contains an ideal
contains an ideal 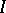 of positive height with the Cohen–Macaulay Rees algebra
of positive height with the Cohen–Macaulay Rees algebra 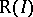 , provided
, provided 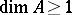 and all the formal fibres of
and all the formal fibres of 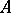 are Cohen–Macaulay. Hence, the Sharp conjecture [a34] concerning the existence of dualizing complexes is solved affirmatively.
are Cohen–Macaulay. Hence, the Sharp conjecture [a34] concerning the existence of dualizing complexes is solved affirmatively.
Let 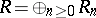 be a Noetherian graded ring with
be a Noetherian graded ring with  a field and let
a field and let 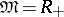 . Then
. Then 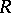 is a Buchsbaum ring if and only if the local ring
is a Buchsbaum ring if and only if the local ring 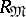 is Buchsbaum. When this is the case, the local cohomology modules
is Buchsbaum. When this is the case, the local cohomology modules 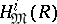 (
( ) are finite-dimensional vector spaces over the field
) are finite-dimensional vector spaces over the field 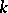 . The vanishing of certain homogeneous components
. The vanishing of certain homogeneous components 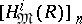 of
of 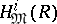 may affect the Buchsbaumness in graded algebras
may affect the Buchsbaumness in graded algebras 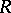 . For example, if there exist integers
. For example, if there exist integers 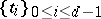 (
(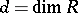 ) such that
) such that 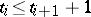 for all
for all 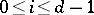 and if
and if
 |
for all 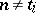 and
and 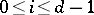 , then
, then 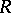 is a Buchsbaum ring [a9]. Therefore
is a Buchsbaum ring [a9]. Therefore 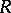 is a Buchsbaum ring if
is a Buchsbaum ring if 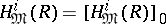 for all
for all 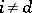 [a33]. Hence the scheme
[a33]. Hence the scheme 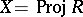 is arithmetically Buchsbaum if
is arithmetically Buchsbaum if 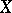 is locally Cohen–Macaulay, provided that
is locally Cohen–Macaulay, provided that 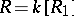 and
and 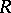 is equi-dimensional. See [a22] for the bounds of Castelnuovo–Mumford regularities of Buchsbaum schemes
is equi-dimensional. See [a22] for the bounds of Castelnuovo–Mumford regularities of Buchsbaum schemes 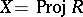 .
.
Researches of the Buchsbaumness in Rees algebras recently (1999) started again, although the progress remains tardy (possibly because of the lack of characterizations of Trung–Ikeda type [a38] for Buchsbaumness). In [a14] the Buchsbaumness in Rees algebras  of certain
of certain 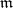 -primary ideals
-primary ideals 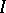 in Cohen–Macaulay local rings is closely studied in connection with the Buchsbaumness in the associated graded rings
in Cohen–Macaulay local rings is closely studied in connection with the Buchsbaumness in the associated graded rings 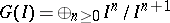 and that of the extended Rees algebras
and that of the extended Rees algebras 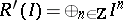 . In [a26], [a41], [a42], Buchsbaumness in graded rings associated to certain
. In [a26], [a41], [a42], Buchsbaumness in graded rings associated to certain 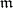 -primary ideals in Buchsbaum local rings is explored. Especially, the Rees algebra
-primary ideals in Buchsbaum local rings is explored. Especially, the Rees algebra 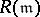 of the maximal ideal
of the maximal ideal 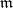 in a Buchsbaum local ring
in a Buchsbaum local ring 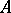 of maximal embedding dimension (that is, a Buchsbaum local ring
of maximal embedding dimension (that is, a Buchsbaum local ring 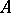 for which the equality
for which the equality 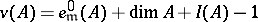 holds) is again a Buchsbaum ring [a42].
holds) is again a Buchsbaum ring [a42].
References
| [a1] | M. Amasaki, "Existence of homogeneous prime ideals fitting into long Bourbaki sequences" , Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999 (1999) pp. 104–111 |
| [a2] | J. Barshay, "Graded algebras of powers of ideals generated by A-sequences" J. Algebra , 25 (1973) pp. 90–99 |
| [a3] | D.A. Buchsbaum, "Complexes in local ring theory" , Some Aspects of Ring Theory , C.I.M.E. Roma (1965) pp. 223–228 |
| [a4] | G. Eisenbud, S. Goto, "Linear free resolutions and minimal multiplicity" J. Algebra , 88 (1984) pp. 89–133 |
| [a5] | E.G. Evans Jr., P.A. Griffith, "Local cohomology modules for normal domains" J. London Math. Soc. , 19 (1979) pp. 277–284 |
| [a6] | S. Goto, "On Buchsbaum rings" J. Algebra , 67 (1980) pp. 272–279 |
| [a7] | S. Goto, "Blowing-up of Buchsbaum rings" , Commutative Algebra , Lecture Notes , 72 , London Math. Soc. (1981) pp. 140–162 |
| [a8] | S. Goto, "Buchsbaum rings with multiplicity 2" J. Algebra , 74 (1982) pp. 494–508 |
| [a9] | S. Goto, "Buchsbaum rings of maximal embedding dimension" J. Algebra , 76 (1982) pp. 383–399 |
| [a10] | S. Goto, "On the associated graded rings of parameter ideals in Buchsbaum rings" J. Algebra , 85 (1983) pp. 490–534 |
| [a11] | S. Goto, "Surface singularities of finite Buchsbaum-representation type" , Commutative Algebra: Proc. Microprogram June 15–July 2 , Springer (1987) pp. 247–263 |
| [a12] | S. Goto, "Maximal Buchsbaum modules over regular local rings and a structure theorem for generalized Cohen–Macaulay modules" M. Nagata (ed.) H. Matsumura (ed.) , Commutative Algebra and Combinatorics , Adv. Stud. Pure Math. , 11 , Kinokuniya (1987) pp. 39–46 |
| [a13] | S. Goto, "Curve singularities of finite Buchsbaum-representation type" J. Algebra , 163 (1994) pp. 447–480 |
| [a14] | S. Goto, "Buchsbaumness in Rees algebras associated to ideals of minimal multiplicity" J. Algebra , 213 (1999) pp. 604–661 |
| [a15] | S. Goto, K. Nishida, "Rings with only finitely many isomorphism classes of indecomposable maximal Buchsbaum modules" J. Math. Soc. Japan , 40 (1988) pp. 501–518 |
| [a16] | S. Goto, K. Nishida, "The Cohen–Macaulay and Gorenstein Rees algebras associated to filtrations" , Memoirs , 526 , Amer. Math. Soc. (1994) |
| [a17] | S. Goto, Y. Nakamura, K. Nishida, "Cohen–Macaulay graded rings associated ideals" Amer. J. Math. , 118 (1996) pp. 1197–1213 |
| [a18] | S. Goto, Y. Shimoda, "On the Rees algebras of Cohen–Macaulay local rings" R.N. Draper (ed.) , Commutative Algebra, Analytic Methods , Lecture Notes in Pure Applied Math. , 68 , M. Dekker (1982) pp. 201–231 |
| [a19] | S. Goto, Y. Shimoda, "On Rees algebras over Buchsbaum rings" J. Math. Kyoto Univ. , 20 (1980) pp. 691–708 |
| [a20] | S. Goto, K. Yamagishi, "The theory of unconditioned strong 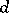 -sequences and modules of finite local cohomology" Preprint (1978) -sequences and modules of finite local cohomology" Preprint (1978) |
| [a21] | C. Huneke, "The theory of d-sequences and powers of ideals" Adv. Math. , 46 (1982) pp. 249–279 |
| [a22] | L.T. Hoa, C. Miyazaki, "Bounds on Castelnuovo–Mumford regularity for generalized Cohen–Macaulay graded rings" Math. Ann. , 301 (1995) pp. 587–598 |
| [a23] | M.-N. Ishida, "Tsuchihashi's cusp singularities are Buchsbaum singularities" Tôhoku Math. J. , 36 (1984) pp. 191–201 |
| [a24] | T. Kawasaki, "Local cohomology modules of indecomposable surjective–Buchsbaum modules over Gorenstein local rings" J. Math. Soc. Japan , 48 (1996) pp. 551–566 |
| [a25] | T. Kawasaki, "Arithmetic Cohen–Macaulayfications of local rings" , Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999 (1999) pp. 88–92 |
| [a26] | Y. Nakamura, "On the Buchsbaum property of associated graded rings" J. Algebra , 209 (1998) pp. 345–366 |
| [a27] | P. Schenzel, N.V. Trung, N.T. Cuong, "Verallgemeinerte Cohen–Macaulay-Moduln" Math. Nachr. , 85 (1978) pp. 57–73 |
| [a28] | J. Stückrad, W. Vogel, "Ein Korrekturglied in der Multiplizitätstheorie von D.G. Northcott und Anwendungen" Monatsh. Math. , 76 (1972) pp. 264–271 |
| [a29] | J. Stückrad, W. Vogel, "Eine Verallgemeinerung der Cohen–Macaulay-Ringe und Anwendungen auf ein Problem der Multiplitätstheorie" J. Math. Kyoto Univ. , 13 (1973) pp. 513–528 |
| [a30] | J. Stückrad, W. Vogel, "Toward a theory of Buchsbaum singularities" Amer. J. Math. , 100 (1978) pp. 727–746 |
| [a31] | J. Stückrad, W. Vogel, "Buchsbaum rings and applications" , Springer (1986) |
| [a32] | P. Schenzel, "Dualisierende Komplexe in der lokalen Algebra und Buchsbaum–Ringe" , Lecture Notes in Mathematics , 907 , Springer (1982) |
| [a33] | P. Schenzel, "On Veronesean embeddings and projections of Veronesean varieties" Archiv Math. , 30 (1978) pp. 391–397 |
| [a34] | R.Y. Sharp, "Necessary conditions for the existence of dualizing complexes in commutative algebra" , Lecture Notes in Mathematics , 740 , Springer (1979) pp. 213–229 |
| [a35] | Y. Shimoda, "A note on Rees algebras of two-dimensional local domains" J. Math. Kyoto Univ. , 19 (1979) pp. 327–333 |
| [a36] | J. Stückrad, "On the Buchsbaum property of Rees and form modules" Beitr. Algebra Geom. , 19 (1985) pp. 83–103 |
| [a37] | N.V. Trung, "Toward a theory of generalized Cohen–Macaulay modules" Nagoya Math. J. , 102 (1986) pp. 1–49 |
| [a38] | N.V. Trung, S. Ikeda, "When is the Rees algebra Cohen–Macaulay?" Commun. Algebra , 17 (1989) pp. 2893–2922 |
| [a39] | W. Vasconcelos, "Arithmetic of blowup algebras" , London Math. Soc. Lecture Notes , 195 , Cambridge Univ. Press (1994) |
| [a40] | Y. Yoshino, "Maximal Buchsbaum modules of finite projective dimension" J. Algebra , 159 (1993) pp. 240–264 |
| [a41] | K. Yamagishi, "The associated graded modules of Buchsbaum modules with respect to 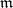 -primary ideals in equi-I-invariant case" J. Algebra , 225 (2000) pp. 1–27 -primary ideals in equi-I-invariant case" J. Algebra , 225 (2000) pp. 1–27 |
| [a42] | K. Yamagishi, "Buchsbaumness in Rees algebras associated to 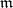 -primary ideals of minimal multiplicity in Buchsbaum local rings" , Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999 (1999) pp. 39–45 -primary ideals of minimal multiplicity in Buchsbaum local rings" , Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999 (1999) pp. 39–45 |
Buchsbaum ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buchsbaum_ring&oldid=16254