Brauer characterization of characters
Let 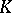 be a field, let
be a field, let 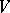 be a finite-dimensional vector space over
be a finite-dimensional vector space over 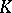 and let
and let 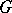 be a finite group. A representation of
be a finite group. A representation of 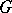 over
over 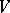 is a group homomorphism
is a group homomorphism 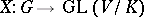 (the group of
(the group of 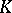 -linear automorphisms of
-linear automorphisms of 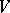 ) or, equivalently, a module action of the group algebra
) or, equivalently, a module action of the group algebra 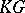 on
on 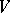 (the equivalence is defined by:
(the equivalence is defined by: 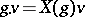 for all
for all 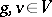 ; cf. also Representation of a group). The character
; cf. also Representation of a group). The character 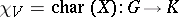 is defined by:
is defined by: 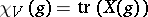 for all
for all 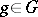 . Since
. Since 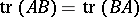 for any two
for any two 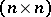 -matrices
-matrices 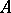 ,
, 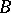 over
over 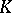 , one finds that
, one finds that 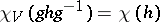 for all
for all 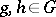 , and hence
, and hence 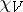 is a class function on
is a class function on 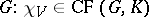 . Equivalent representations have the same character and
. Equivalent representations have the same character and 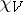 is the sum of the characters of the quotient
is the sum of the characters of the quotient 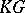 -modules in any
-modules in any 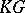 -filtration of
-filtration of 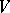 . If
. If 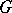 acts irreducibly on
acts irreducibly on 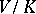 , then
, then 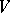 is said to be an irreducible
is said to be an irreducible  -module and
-module and 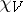 is said to be an irreducible character.
is said to be an irreducible character.
If 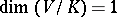 , then
, then 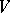 is said to be a linear representation of
is said to be a linear representation of 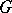 , and
, and 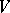 is an irreducible
is an irreducible 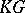 -module;
-module; 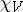 is said to be a linear character. There are at most
is said to be a linear character. There are at most 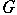 inequivalent types of irreducible representations of
inequivalent types of irreducible representations of 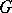 over
over 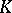 . Let
. Let 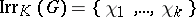 be the set of irreducible characters of
be the set of irreducible characters of 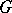 over
over 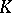 . Then
. Then 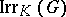 is
is 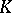 -linearly independent in
-linearly independent in 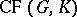 and every character of
and every character of 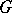 over
over 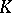 is a sum of elements of
is a sum of elements of 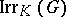 .
.
Let 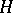 be a subgroup of
be a subgroup of 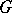 and let
and let 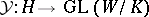 be a representation of
be a representation of 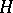 . Clearly, the restriction to
. Clearly, the restriction to 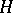 ,
, 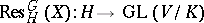 , is a representation of
, is a representation of 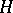 and induction to
and induction to 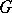 ,
, 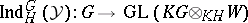 , is a representation of
, is a representation of 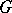 (cf. also Induced representation). If
(cf. also Induced representation). If 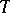 is a transversal for the right cosets of
is a transversal for the right cosets of 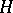 in
in 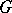 , then, for
, then, for 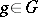 ,
,
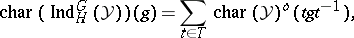 |
where 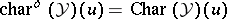 if
if  and
and 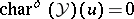 if
if 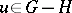 .
.
If 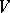 and
and 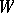 are
are 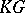 -modules, then
-modules, then 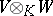 is a
is a 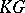 -module defined by "diagonal action" :
-module defined by "diagonal action" :
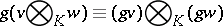 |
for all 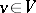 ,
, 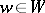 and
and 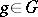 , and
, and 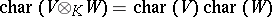 .
.
Assume that 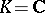 , the field of complex numbers. Then
, the field of complex numbers. Then 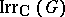 is a
is a 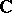 -basis of
-basis of 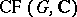 . Also, every
. Also, every 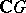 -module
-module 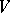 is completely reducible (i.e., a direct sum of irreducible submodules). Also,
is completely reducible (i.e., a direct sum of irreducible submodules). Also, 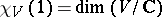 ,
, 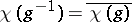 (complex conjugate) and
(complex conjugate) and 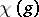 is a sum of
is a sum of 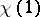
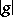 -th roots of unity for all
-th roots of unity for all 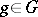 . Also, there is a non-singular symmetric scalar product
. Also, there is a non-singular symmetric scalar product 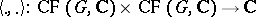 defined by:
defined by:
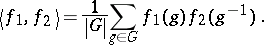 |
Here, 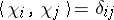 (the Kronecker delta) for all
(the Kronecker delta) for all 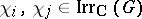 and if
and if 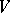 and
and 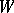 are two finite-dimensional
are two finite-dimensional 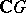 -modules, then
-modules, then 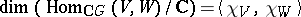 and hence the isomorphism type of
and hence the isomorphism type of 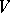 is determined by
is determined by 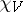 .
.
If 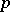 is a prime integer, then a finite group that is the direct product of a cyclic group and a
is a prime integer, then a finite group that is the direct product of a cyclic group and a 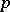 -group (or equivalently of a cyclic
-group (or equivalently of a cyclic 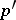 -group and a
-group and a  -group) is called a
-group) is called a 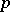 -elementary group. Any subgroup or quotient of such a group is also
-elementary group. Any subgroup or quotient of such a group is also 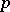 -elementary. A finite group is called elementary if it is
-elementary. A finite group is called elementary if it is 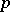 -elementary for some prime number
-elementary for some prime number 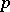 . It is well-known that each irreducible character
. It is well-known that each irreducible character 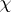 of an elementary group
of an elementary group  is of the form
is of the form 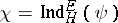 for some subgroup
for some subgroup  of
of 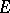 and some linear character
and some linear character 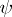 of
of 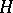 (cf. [a8], Thm. 16).
(cf. [a8], Thm. 16).
For a finite group 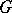 , let
, let  be the additive subgroup of
be the additive subgroup of 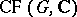 generated by all characters of
generated by all characters of 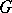 . The elements of
. The elements of 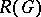 are called virtual or generalized characters of
are called virtual or generalized characters of 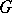 and
and 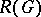 is a ring and also a free Abelian group with free basis
is a ring and also a free Abelian group with free basis 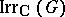 . Clearly,
. Clearly,
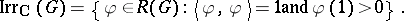 |
In [a2], R. Brauer proved the following assertions:
1) Every character 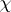 of a finite group
of a finite group 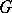 is a linear combination with integer coefficients of characters induced from linear characters of elementary subgroups of
is a linear combination with integer coefficients of characters induced from linear characters of elementary subgroups of 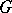 .
.
Brauer used this result in [a2] to prove that Artin  -functions of virtual characters have a meromorphic extension to the entire complex plane. Then, in [a3], he proved that this assertion is equivalent to what is known as the Brauer characterization of characters:
-functions of virtual characters have a meromorphic extension to the entire complex plane. Then, in [a3], he proved that this assertion is equivalent to what is known as the Brauer characterization of characters:
2) A class function 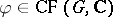 lies in
lies in 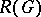 if and only if
if and only if 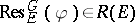 for every elementary subgroup
for every elementary subgroup 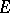 of
of 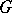 .
.
An immediate consequence (cf. [a8], Thm 22 and Corollary) is:
3) A class function 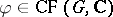 lies in
lies in 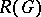 if and only if for each elementary subgroup
if and only if for each elementary subgroup 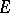 of
of 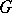 and each linear character
and each linear character  of
of 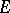 ,
,
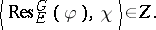 |
A sort of converse of 1) was given by J. Green ([a8], Thm. 23{}). There are numerous applications of these results (cf. [a7], Lemma 8.14; Thm. 8.24, [a6], V, Hauptsatz 19.11, [a8], Sect. 11.2; Chap. 12).
Significant improvements to the proofs of these results have been obtained by several authors [a4], [a7], Chap. 8, [a8], Chaps. 10, 11, [a6], V, Sect. 19.
Let 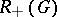 denote the free Abelian group whose free basis is given by the
denote the free Abelian group whose free basis is given by the  -conjugacy classes
-conjugacy classes 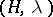 , where
, where 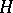 is a subgroup of
is a subgroup of 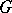 and
and 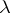 is a linear character of
is a linear character of  . Clearly
. Clearly 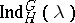 is a character of
is a character of  and hence induction induces an Abelian group homomorphism
and hence induction induces an Abelian group homomorphism 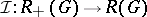 , which is surjective by 1). Some interesting recent results in [a9] and [a1] give explicit (functorial) splittings of
, which is surjective by 1). Some interesting recent results in [a9] and [a1] give explicit (functorial) splittings of 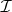 (i.e., an explicit group homomorphism
(i.e., an explicit group homomorphism  such that
such that 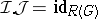 ).
).
Clearly, 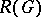 is the Grothendieck group of the category of finitely generated
is the Grothendieck group of the category of finitely generated 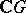 -modules. Consequently, 1) can be viewed as proving the surjectivity of the induction mapping from one Grothendieck group into another. By changing the coefficient ring
-modules. Consequently, 1) can be viewed as proving the surjectivity of the induction mapping from one Grothendieck group into another. By changing the coefficient ring 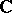 , or by considering the modular context, etc., many important analogues of these results emerge, cf. [a8], Chaps. 12, 16, 17, [a5], Thm. 2, [a10].
, or by considering the modular context, etc., many important analogues of these results emerge, cf. [a8], Chaps. 12, 16, 17, [a5], Thm. 2, [a10].
References
| [a1] | R. Boltje, "A canonical Brauer induction formula" Asterisque , 181/2 (1990) pp. 31–59 |
| [a2] | R. Brauer, "On Artin's  -series with general group characters" Ann. of Math. , 48 (1947) pp. 502–514 -series with general group characters" Ann. of Math. , 48 (1947) pp. 502–514 |
| [a3] | R. Brauer, "A characterization of the characters of a group of finite order" Ann. of Math. , 57 (1953) pp. 357–377 |
| [a4] | R. Brauer, J. Tate, "On the characters of finite groups" Ann. of Math. , 62 (1955) pp. 1–7 |
| [a5] | M. Broué, "Sur l'induction des modules indecomposables et la projectraité relative" Math. Z. , 149 (1976) pp. 227–245 |
| [a6] | B. Huppert, "Endliche Gruppen" , I , Springer (1967) pp. Chapt. V |
| [a7] | I.M. Isaacs, "Character theory of finite groups" , Acad. Press (1976) |
| [a8] | J.-P. Serre, "Linear representations of finite groups" , Springer (1977) (Translated from French) |
| [a9] | V. Snaith, "Explicit Brauer induction" Invent. Math. , 94 (1988) pp. 455–478 |
| [a10] | X. Zhou, "On the decomposition map of Grothendieck groups" Math. Z. , 206 (1991) pp. 533–534 |
Brauer characterization of characters. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brauer_characterization_of_characters&oldid=18401