In 1949, while studying the Betti number of a Kähler manifold, S. Bochner [a1] (see also [a26]), ad hoc and without giving any intrinsic geometric interpretation for its meaning or origin, introduced a new tensor as an analogue of the Weyl conformal curvature tensor in a Riemannian manifold. In a complex local coordinate system in a 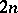 -dimensional Kählerian manifold
-dimensional Kählerian manifold 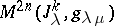 , it is defined as follows:
, it is defined as follows:
where 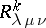 ,
, 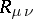 and
and 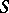 are the Riemannian curvature tensor (cf. Riemann tensor), the Ricci tensor, and the scalar curvature tensor, respectively. This tensor is nowadays called the Bochner curvature tensor.
are the Riemannian curvature tensor (cf. Riemann tensor), the Ricci tensor, and the scalar curvature tensor, respectively. This tensor is nowadays called the Bochner curvature tensor.
In 1967, S. Tachibana [a16] gave a tensorial expression for 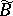 in a real coordinate system in a complex
in a real coordinate system in a complex  -dimensional (
-dimensional (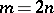 ) Kähler manifold
) Kähler manifold 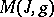 , as follows:
, as follows:
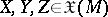 (here,
(here, 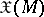 denotes the Lie algebra of vector fields on
denotes the Lie algebra of vector fields on 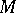 ), where
), where 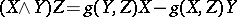 , and
, and 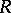 ,
, 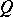 and
and 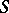 are the Riemannian curvature tensor, the Ricci operator, and the scalar curvature on
are the Riemannian curvature tensor, the Ricci operator, and the scalar curvature on 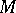 , respectively. Bochner proved that
, respectively. Bochner proved that 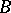 has the components of
has the components of 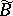 with respect to complex local coordinates. So,
with respect to complex local coordinates. So, 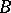 is also called the Bochner curvature tensor. Since then the tensors
is also called the Bochner curvature tensor. Since then the tensors 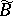 and
and 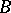 have been intensively studied on Kähler manifolds; see, e.g., [a3], [a16], [a17], [a22], [a23], [a24], [a25], [a26], [a27], [a28] (in particular, in [a22]
have been intensively studied on Kähler manifolds; see, e.g., [a3], [a16], [a17], [a22], [a23], [a24], [a25], [a26], [a27], [a28] (in particular, in [a22]  is identified with the fourth-order Chern–Moser tensor [a4] for CR-manifolds.)
is identified with the fourth-order Chern–Moser tensor [a4] for CR-manifolds.)
Generalization.
M. Sitaramayya [a15] and H. Mori [a12] obtained a generalized Bochner curvature tensor 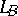 as a component in its curvature tensor
as a component in its curvature tensor 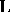 by considering the decomposition theory of spaces of the generalized curvature tensor
by considering the decomposition theory of spaces of the generalized curvature tensor 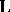 on a real
on a real 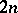 -dimensional Kählerian vector space
-dimensional Kählerian vector space  , using the method of I.M. Singer and J.A. Thorpe [a14] (see also [a13]). If
, using the method of I.M. Singer and J.A. Thorpe [a14] (see also [a13]). If  is a Kähler manifold and
is a Kähler manifold and 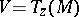 , then
, then 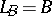 .
.
F. Tricerri and L. Vanhecke [a21] generalized this notion, that is, they succeeded in defining the generalized Bochner curvature tensor 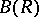 as a component of the element of spaces of arbitrary generalized curvature tensors
as a component of the element of spaces of arbitrary generalized curvature tensors 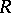 on a real
on a real 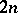 -dimensional Hermitian vector space
-dimensional Hermitian vector space 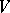 . Of course, when
. Of course, when 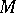 is a Kähler manifold and
is a Kähler manifold and 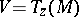 ,
, 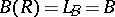 . Moreover, they also showed that, like the case of the Weyl tensor,
. Moreover, they also showed that, like the case of the Weyl tensor, 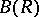 is invariant under conformal changes (
is invariant under conformal changes (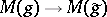 ,
, 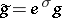 , where
, where 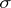 is a
is a 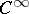 -function on
-function on 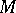 ) in an arbitrary almost-Hermitian manifold
) in an arbitrary almost-Hermitian manifold 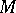 . In this context it means that they gave a geometrical interpretation of the Bochner curvature tensor. These results also show
. In this context it means that they gave a geometrical interpretation of the Bochner curvature tensor. These results also show 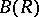 to be a complete generalization of the Bochner curvature tensor on Kählerian manifolds to Hermitian manifolds (cf. also Hermitian structure). Some interesting applications for
to be a complete generalization of the Bochner curvature tensor on Kählerian manifolds to Hermitian manifolds (cf. also Hermitian structure). Some interesting applications for 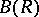 have also been given.
have also been given.
Bochner curvature tensor on contact metric manifolds.
In 1969, M. Matsumoto and G. Chūman [a11] (see also [a25]) defined on a 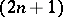 -dimensional Sasakian manifold
-dimensional Sasakian manifold 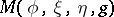 the contact Bochner curvature tensor, which is constructed from the Bochner curvature tensor in a Kählerian manifold by considering the Boothby–Wang fibering [a2]. It is as follows:
the contact Bochner curvature tensor, which is constructed from the Bochner curvature tensor in a Kählerian manifold by considering the Boothby–Wang fibering [a2]. It is as follows:
where  ,
, 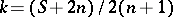 . They called this tensor the
. They called this tensor the 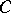 -Bochner tensor. Then they also proved that the
-Bochner tensor. Then they also proved that the 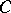 -Bochner tensor is invariant under
-Bochner tensor is invariant under 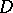 -homothetic deformations
-homothetic deformations 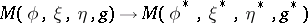 ,
, 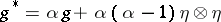 ,
, 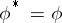 ,
, 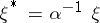 ,
, 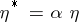 ,
, 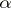 a positive constant (see [a19]), on a Sasakian manifold. After that many papers about
a positive constant (see [a19]), on a Sasakian manifold. After that many papers about 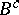 on Sasakian manifolds were published; see, e.g., [a5], [a11], [a25], [a28].
on Sasakian manifolds were published; see, e.g., [a5], [a11], [a25], [a28].
The tensor 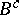 is generally not invariant under
is generally not invariant under 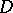 -homothetic deformations in more general manifolds, for example
-homothetic deformations in more general manifolds, for example 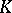 -contact Riemannian manifolds and contact metric manifolds. So, a natural problem arises here: Is it possible to construct a "Bochner curvature tensor" for manifolds of more general classes than Sasakian manifolds?
-contact Riemannian manifolds and contact metric manifolds. So, a natural problem arises here: Is it possible to construct a "Bochner curvature tensor" for manifolds of more general classes than Sasakian manifolds?
In 1991, H. Endo [a6] defined on a 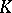 -contact Riemannian manifold the
-contact Riemannian manifold the 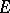 -contact Bochner curvature tensor, constructed from
-contact Bochner curvature tensor, constructed from 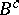 . The
. The 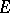 -contact Bochner curvature tensor is invariant under
-contact Bochner curvature tensor is invariant under 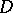 -homothetic deformations on a
-homothetic deformations on a 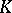 -contact Riemannian manifold and becomes
-contact Riemannian manifold and becomes 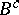 on a Sasakian manifold. He also showed that a
on a Sasakian manifold. He also showed that a 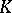 -contact Riemannian manifold with vanishing
-contact Riemannian manifold with vanishing 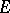 -contact Bochner curvature tensor is Sasakian. Moreover, in 1993 he constructed [a7] on a manifold of more general class than
-contact Bochner curvature tensor is Sasakian. Moreover, in 1993 he constructed [a7] on a manifold of more general class than 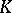 -contact Riemannian manifolds (to wit, a contact metric manifold), an extended contact Bochner curvature tensor by using a new tensor
-contact Riemannian manifolds (to wit, a contact metric manifold), an extended contact Bochner curvature tensor by using a new tensor 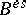 which modified
which modified 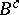 . It is called the
. It is called the 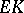 -contact Bochner curvature tensor. Of course, the
-contact Bochner curvature tensor. Of course, the 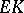 -contact Bochner curvature tensor coincides with
-contact Bochner curvature tensor coincides with 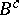 on a Sasakian manifold and is invariant under
on a Sasakian manifold and is invariant under 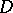 -homothetic deformations on a contact metric manifold. Furthermore, he proved that contact metric manifolds with vanishing
-homothetic deformations on a contact metric manifold. Furthermore, he proved that contact metric manifolds with vanishing 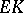 -contact Bochner curvature tensor are Sasakian (see [a8] for another study on
-contact Bochner curvature tensor are Sasakian (see [a8] for another study on 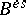 ).
).
Bochner curvature tensor on almost-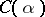 manifolds.
manifolds.
D. Janssens and L. Vanhecke [a10] defined a Bochner curvature tensor on a class of almost-contact metric manifolds, i.e., almost-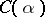 manifolds, containing Sasakian manifolds, Kemmotsu manifolds, and co-symplectic manifolds (cf. [a10]) with a decomposition theory of spaces of a class of the generalized curvature tensor on a real vector space. Some geometrical applications were also given.
manifolds, containing Sasakian manifolds, Kemmotsu manifolds, and co-symplectic manifolds (cf. [a10]) with a decomposition theory of spaces of a class of the generalized curvature tensor on a real vector space. Some geometrical applications were also given.
Modified contact Bochner curvature tensor on almost co-symplectic manifolds.
Endo [a9] considered a tensor which modifies 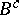 and introduced a new modified contact Bochner curvature tensor which is invariant with respect to
and introduced a new modified contact Bochner curvature tensor which is invariant with respect to 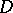 -homothetic deformations on an almost co-symplectic manifold
-homothetic deformations on an almost co-symplectic manifold 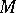 . He called it the
. He called it the 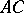 -contact Bochner curvature tensor. If
-contact Bochner curvature tensor. If 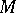 is a co-symplectic manifold, the
is a co-symplectic manifold, the 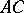 -contact Bochner curvature turns into the main part of
-contact Bochner curvature turns into the main part of 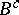 . He also studied almost co-symplectic manifolds with vanishing
. He also studied almost co-symplectic manifolds with vanishing 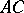 -contact Bochner curvature tensor.
-contact Bochner curvature tensor.
Bochner-type curvature tensor on the space defined by 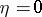 .
.
In 1988, S. Tanno [a20] defined on a contact metric manifold 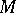 the Bochner-type curvature tensor (
the Bochner-type curvature tensor (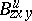 ) for the space defined by
) for the space defined by 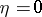 , in such a way that its change under gauge transformations (
, in such a way that its change under gauge transformations (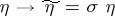 ,
, 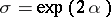 is a positive function on
is a positive function on  ) is natural; it has a generalized form of the Chern–Moser–Tanaka invariant [a4], [a18] (
) is natural; it has a generalized form of the Chern–Moser–Tanaka invariant [a4], [a18] (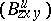 is not a tensor on
is not a tensor on 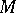 ). From this he obtained a relation between
). From this he obtained a relation between 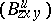 and the
and the 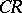 -structure corresponding to
-structure corresponding to 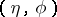 .
.
References
| [a1] | S. Bochner, "Curvature and Betti numbers II" Ann. of Math. , 50 (1949) pp. 77–93 |
| [a2] | W.M. Boothby, H.C. Wang, "On contact manifolds" Ann. of Math. , 68 (1958) pp. 721–734 |
| [a3] | B.Y. Chen, K. Yano, "Manifolds with vanishing Weyl or Bochner curvature tensor" J. Math. Soc. Japan , 27 (1975) pp. 106–112 |
| [a4] | S.S. Chern, J.K. Moser, "Real hypersurfaces in complex manifolds" Acta Math. , 133 (1974) pp. 219–271 |
| [a5] | H. Endo, "On anti-invariant submanifolds in Sasakian manifolds with vanishing contact Bochner curvature tensor" Publ. Math. Debrecen , 38 (1991) pp. 263–271 |
| [a6] | H. Endo, "On 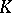 -contact Riemannian manifolds with vanishing -contact Riemannian manifolds with vanishing 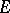 -contact Bochner curvature tensor" Colloq. Math. , 62 (1991) pp. 293–297 -contact Bochner curvature tensor" Colloq. Math. , 62 (1991) pp. 293–297 |
| [a7] | H. Endo, "On an extended contact Bochner curvature tensor on contact metric manifolds" Colloq. Math. , 65 (1993) pp. 33–41 |
| [a8] | H. Endo, "On certain tensor fields on contact metric manifolds. II" Publ. Math. Debrecen , 44 (1994) pp. 157–166 |
| [a9] | H. Endo, "On the 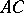 -contact Bochner curvature tensor field on almost cosymplectic manifolds" Publ. Inst. Math. (Beograd) (N.S.) , 56 (1994) pp. 102–110 -contact Bochner curvature tensor field on almost cosymplectic manifolds" Publ. Inst. Math. (Beograd) (N.S.) , 56 (1994) pp. 102–110 |
| [a10] | D. Janssens, L. Vanhecke, "Almost contact structures and curvature tensors" Kodai Math. J. , 4 (1981) pp. 1–27 |
| [a11] | M. Matsumoto, G. Chūman, "On the 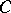 -Bochner curvature tensor" TRU. Math. , 5 (1967) pp. 21–30 -Bochner curvature tensor" TRU. Math. , 5 (1967) pp. 21–30 |
| [a12] | H. Mori, "On the decomposition of generalized 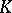 -curvature tensor fields" Tôhoku Math. J. , 25 (1973) pp. 225–235 -curvature tensor fields" Tôhoku Math. J. , 25 (1973) pp. 225–235 |
| [a13] | K. Nomizu, "On the decomposition of generalized curvature tensor fields" , Differential Geometry (In Honour of K. Yano) , Kinokuniya (1972) pp. 335–345 |
| [a14] | I.M. Singer, J.A. Thorpe, "The curvature of 4-dimensional Einstein spaces" , Global Analysis (In Honour of K. Kodaira) , Univ. Tokyo Press (1969) pp. 355–365 |
| [a15] | M. Sitaramayya, "Curvature tensors in Kähler manifolds" Trans. Amer. Math. Soc. , 183 (1973) pp. 341–353 |
| [a16] | S. Tachibana, "On the Bochner curvature tensor" Natur. Sci. Rep. Ochanomizu Univ. , 18 (1967) pp. 15–19 |
| [a17] | S. Tachibana, R.C. Liu, "Notes on Kaehlerian metrics with vanishing Bochner curvature tensor" Kōdai Math. Sem. Rep. , 22 (1970) pp. 313–321 |
| [a18] | N. Tanaka, "On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections" Japan. J. Math. (N.S.) , 2 (1976) pp. 131–190 |
| [a19] | S. Tanno, "Partially conformal transformations with respect to 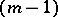 -dimensional distributions of -dimensional distributions of 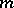 -dimensional Riemannian manifolds" Tôhoku Math. J. , 17 (1965) pp. 358–409 -dimensional Riemannian manifolds" Tôhoku Math. J. , 17 (1965) pp. 358–409 |
| [a20] | S. Tanno, "The Bochner type curvature tensor of contact Riemannian structure" Hokkaido Math. J. , 19 (1990) pp. 55–66 |
| [a21] | F. Tricerri, L. Vanhecke, "Curvature tensors on almost Hermitian manifolds" Trans. Amer. Math. Soc. , 267 (1981) pp. 365–398 |
| [a22] | S.M. Webster, "On the pseudo-conformal geometry of a Kaehler manifold" Math. Z. , 157 (1977) pp. 265–270 |
| [a23] | K. Yano, "Manifolds and submanifolds with vanishing Weyl or Bochner curvature tensor" , Proc. Symp. Pure Math. , 27 , Amer. Math. Soc. (1975) pp. 253–262 |
| [a24] | K. Yano, "Differential geometry of totally real submanifolds" , Topics in Differential Geometry , Acad. Press (1976) pp. 173–184 |
| [a25] | K. Yano, "Anti-invariant submanifolds of a Sasakian manifold with vanishing contact Bochner curvature tensor" J. Diff. Geom. , 12 (1977) pp. 153–170 |
| [a26] | K. Yano, S. Bochner, "Curvature and Betti numbers" , Annals of Math. Stud. , 32 , Princeton Univ. Press (1953) |
| [a27] | K. Yano, S. Ishihara, "Kaehlerian manifolds with constant scalar curvature whose Bochner curvature tensor vanishes" Hokkaido Math. J. , 3 (1974) pp. 297–304 |
| [a28] | K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984) |
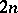 -dimensional Kählerian manifold
-dimensional Kählerian manifold 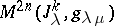 , it is defined as follows:
, it is defined as follows:
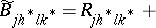

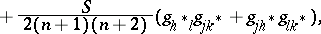
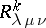 ,
, 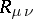 and
and 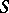 are the Riemannian curvature tensor (cf. Riemann tensor), the Ricci tensor, and the scalar curvature tensor, respectively. This tensor is nowadays called the Bochner curvature tensor.
are the Riemannian curvature tensor (cf. Riemann tensor), the Ricci tensor, and the scalar curvature tensor, respectively. This tensor is nowadays called the Bochner curvature tensor.
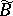 in a real coordinate system in a complex
in a real coordinate system in a complex  -dimensional (
-dimensional (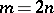 ) Kähler manifold
) Kähler manifold 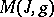 , as follows:
, as follows:
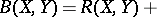
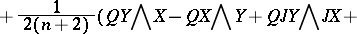
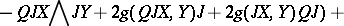
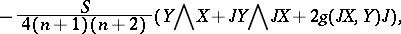
 (here,
(here, 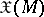 denotes the Lie algebra of vector fields on
denotes the Lie algebra of vector fields on 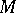 ), where
), where 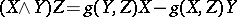 , and
, and 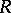 ,
, 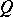 and
and 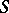 are the Riemannian curvature tensor, the Ricci operator, and the scalar curvature on
are the Riemannian curvature tensor, the Ricci operator, and the scalar curvature on 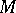 , respectively. Bochner proved that
, respectively. Bochner proved that 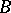 has the components of
has the components of 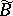 with respect to complex local coordinates. So,
with respect to complex local coordinates. So, 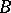 is also called the Bochner curvature tensor. Since then the tensors
is also called the Bochner curvature tensor. Since then the tensors 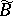 and
and 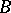 have been intensively studied on Kähler manifolds; see, e.g., [a3], [a16], [a17], [a22], [a23], [a24], [a25], [a26], [a27], [a28] (in particular, in [a22]
have been intensively studied on Kähler manifolds; see, e.g., [a3], [a16], [a17], [a22], [a23], [a24], [a25], [a26], [a27], [a28] (in particular, in [a22]  is identified with the fourth-order Chern–Moser tensor [a4] for CR-manifolds.)
is identified with the fourth-order Chern–Moser tensor [a4] for CR-manifolds.)
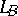 as a component in its curvature tensor
as a component in its curvature tensor 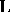 by considering the decomposition theory of spaces of the generalized curvature tensor
by considering the decomposition theory of spaces of the generalized curvature tensor 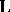 on a real
on a real 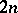 -dimensional Kählerian vector space
-dimensional Kählerian vector space  , using the method of I.M. Singer and J.A. Thorpe [a14] (see also [a13]). If
, using the method of I.M. Singer and J.A. Thorpe [a14] (see also [a13]). If  is a Kähler manifold and
is a Kähler manifold and 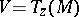 , then
, then 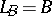 .
.
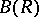 as a component of the element of spaces of arbitrary generalized curvature tensors
as a component of the element of spaces of arbitrary generalized curvature tensors 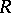 on a real
on a real 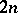 -dimensional Hermitian vector space
-dimensional Hermitian vector space 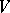 . Of course, when
. Of course, when 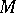 is a Kähler manifold and
is a Kähler manifold and 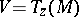 ,
, 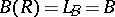 . Moreover, they also showed that, like the case of the Weyl tensor,
. Moreover, they also showed that, like the case of the Weyl tensor, 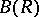 is invariant under conformal changes (
is invariant under conformal changes (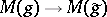 ,
, 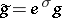 , where
, where 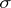 is a
is a 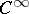 -function on
-function on 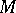 ) in an arbitrary almost-Hermitian manifold
) in an arbitrary almost-Hermitian manifold 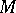 . In this context it means that they gave a geometrical interpretation of the Bochner curvature tensor. These results also show
. In this context it means that they gave a geometrical interpretation of the Bochner curvature tensor. These results also show 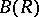 to be a complete generalization of the Bochner curvature tensor on Kählerian manifolds to Hermitian manifolds (cf. also Hermitian structure). Some interesting applications for
to be a complete generalization of the Bochner curvature tensor on Kählerian manifolds to Hermitian manifolds (cf. also Hermitian structure). Some interesting applications for 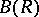 have also been given.
have also been given.
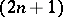 -dimensional Sasakian manifold
-dimensional Sasakian manifold 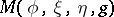 the contact Bochner curvature tensor, which is constructed from the Bochner curvature tensor in a Kählerian manifold by considering the Boothby–Wang fibering [a2]. It is as follows:
the contact Bochner curvature tensor, which is constructed from the Bochner curvature tensor in a Kählerian manifold by considering the Boothby–Wang fibering [a2]. It is as follows:
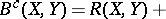
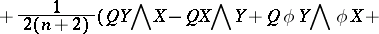
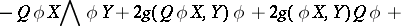
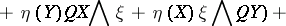
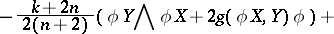

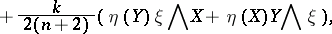
 ,
, 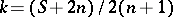 . They called this tensor the
. They called this tensor the 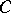 -Bochner tensor. Then they also proved that the
-Bochner tensor. Then they also proved that the 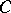 -Bochner tensor is invariant under
-Bochner tensor is invariant under 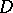 -homothetic deformations
-homothetic deformations 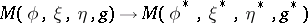 ,
, 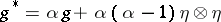 ,
, 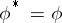 ,
, 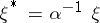 ,
, 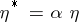 ,
, 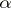 a positive constant (see [a19]), on a Sasakian manifold. After that many papers about
a positive constant (see [a19]), on a Sasakian manifold. After that many papers about 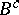 on Sasakian manifolds were published; see, e.g., [a5], [a11], [a25], [a28].
on Sasakian manifolds were published; see, e.g., [a5], [a11], [a25], [a28].
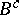 is generally not invariant under
is generally not invariant under 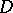 -homothetic deformations in more general manifolds, for example
-homothetic deformations in more general manifolds, for example 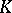 -contact Riemannian manifolds and contact metric manifolds. So, a natural problem arises here: Is it possible to construct a "Bochner curvature tensor" for manifolds of more general classes than Sasakian manifolds?
-contact Riemannian manifolds and contact metric manifolds. So, a natural problem arises here: Is it possible to construct a "Bochner curvature tensor" for manifolds of more general classes than Sasakian manifolds?
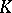 -contact Riemannian manifold the
-contact Riemannian manifold the 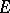 -contact Bochner curvature tensor, constructed from
-contact Bochner curvature tensor, constructed from 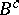 . The
. The 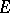 -contact Bochner curvature tensor is invariant under
-contact Bochner curvature tensor is invariant under 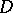 -homothetic deformations on a
-homothetic deformations on a 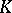 -contact Riemannian manifold and becomes
-contact Riemannian manifold and becomes 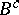 on a Sasakian manifold. He also showed that a
on a Sasakian manifold. He also showed that a 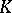 -contact Riemannian manifold with vanishing
-contact Riemannian manifold with vanishing 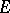 -contact Bochner curvature tensor is Sasakian. Moreover, in 1993 he constructed [a7] on a manifold of more general class than
-contact Bochner curvature tensor is Sasakian. Moreover, in 1993 he constructed [a7] on a manifold of more general class than 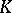 -contact Riemannian manifolds (to wit, a contact metric manifold), an extended contact Bochner curvature tensor by using a new tensor
-contact Riemannian manifolds (to wit, a contact metric manifold), an extended contact Bochner curvature tensor by using a new tensor 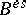 which modified
which modified 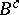 . It is called the
. It is called the 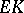 -contact Bochner curvature tensor. Of course, the
-contact Bochner curvature tensor. Of course, the 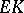 -contact Bochner curvature tensor coincides with
-contact Bochner curvature tensor coincides with 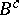 on a Sasakian manifold and is invariant under
on a Sasakian manifold and is invariant under 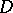 -homothetic deformations on a contact metric manifold. Furthermore, he proved that contact metric manifolds with vanishing
-homothetic deformations on a contact metric manifold. Furthermore, he proved that contact metric manifolds with vanishing 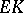 -contact Bochner curvature tensor are Sasakian (see [a8] for another study on
-contact Bochner curvature tensor are Sasakian (see [a8] for another study on 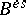 ).
).
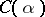 manifolds.
manifolds.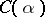 manifolds, containing Sasakian manifolds, Kemmotsu manifolds, and co-symplectic manifolds (cf. [a10]) with a decomposition theory of spaces of a class of the generalized curvature tensor on a real vector space. Some geometrical applications were also given.
manifolds, containing Sasakian manifolds, Kemmotsu manifolds, and co-symplectic manifolds (cf. [a10]) with a decomposition theory of spaces of a class of the generalized curvature tensor on a real vector space. Some geometrical applications were also given.
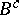 and introduced a new modified contact Bochner curvature tensor which is invariant with respect to
and introduced a new modified contact Bochner curvature tensor which is invariant with respect to 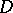 -homothetic deformations on an almost co-symplectic manifold
-homothetic deformations on an almost co-symplectic manifold 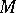 . He called it the
. He called it the 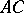 -contact Bochner curvature tensor. If
-contact Bochner curvature tensor. If 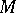 is a co-symplectic manifold, the
is a co-symplectic manifold, the 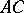 -contact Bochner curvature turns into the main part of
-contact Bochner curvature turns into the main part of 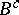 . He also studied almost co-symplectic manifolds with vanishing
. He also studied almost co-symplectic manifolds with vanishing 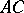 -contact Bochner curvature tensor.
-contact Bochner curvature tensor.
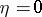 .
.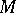 the Bochner-type curvature tensor (
the Bochner-type curvature tensor (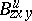 ) for the space defined by
) for the space defined by 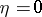 , in such a way that its change under gauge transformations (
, in such a way that its change under gauge transformations (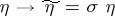 ,
, 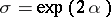 is a positive function on
is a positive function on  ) is natural; it has a generalized form of the Chern–Moser–Tanaka invariant [a4], [a18] (
) is natural; it has a generalized form of the Chern–Moser–Tanaka invariant [a4], [a18] (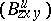 is not a tensor on
is not a tensor on 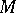 ). From this he obtained a relation between
). From this he obtained a relation between 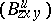 and the
and the 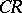 -structure corresponding to
-structure corresponding to 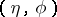 .
.
 -contact Riemannian manifolds with vanishing
-contact Riemannian manifolds with vanishing 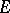 -contact Bochner curvature tensor" Colloq. Math. , 62 (1991) pp. 293–297
-contact Bochner curvature tensor" Colloq. Math. , 62 (1991) pp. 293–297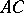 -contact Bochner curvature tensor field on almost cosymplectic manifolds" Publ. Inst. Math. (Beograd) (N.S.) , 56 (1994) pp. 102–110
-contact Bochner curvature tensor field on almost cosymplectic manifolds" Publ. Inst. Math. (Beograd) (N.S.) , 56 (1994) pp. 102–110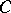 -Bochner curvature tensor" TRU. Math. , 5 (1967) pp. 21–30
-Bochner curvature tensor" TRU. Math. , 5 (1967) pp. 21–30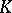 -curvature tensor fields" Tôhoku Math. J. , 25 (1973) pp. 225–235
-curvature tensor fields" Tôhoku Math. J. , 25 (1973) pp. 225–235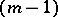 -dimensional distributions of
-dimensional distributions of 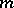 -dimensional Riemannian manifolds" Tôhoku Math. J. , 17 (1965) pp. 358–409
-dimensional Riemannian manifolds" Tôhoku Math. J. , 17 (1965) pp. 358–409