BMO-space

space of functions of bounded mean oscillation

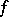Functions of bounded mean oscillation were introduced by F. John and L. Nirenberg [a8], [a12], in connection with differential equations. The definition on reads as follows: Suppose that is integrable over compact sets in 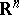, (i.e. ), and that is any ball in 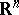, with volume denoted by 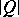. The mean of 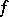over 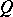will be

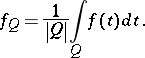By definition, 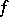belongs to 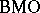if

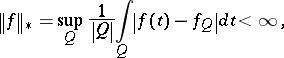where the supremum is taken over all balls 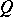. Here, 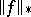is called the 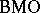-norm of 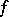, and it becomes a norm on 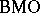after dividing out the constant functions. Bounded functions are in 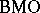and a 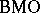-function is locally in 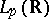for every 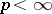. Typical examples of 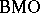-functions are of the form 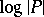with 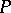a polynomial on .

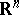The space is very important in modern harmonic analysis. Taking 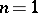, the Hilbert transform 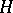, defined by 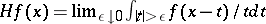, maps 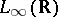to boundedly, i.e.

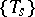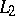The same is true for a large class of singular integral transformations (cf. also Singular integral), including Riesz transformations [a12]. There is a version of the Riesz interpolation theorem (cf. also Riesz interpolation formula) for analytic families of operators , , which besides the -boundedness assumptions on involves the (weak) assumption 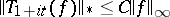instead of the usual assumption 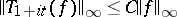, cf. [a12]. However the most famous result is the Fefferman duality theorem, [a6], [a7], [a12]. It states that the dual of 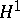is 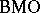. Here, 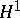denotes the real Hardy space on 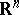(cf. also Hardy spaces). The result is also valid for the usual space 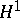on the disc or the upper half-plane, with an appropriate complex multiplication on 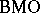, cf. [a5].

Calderón–Zygmund operators on 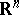form an important class of singular integral operators. A Calderón–Zygmund operator can be defined as a linear operator 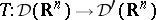with associated Schwarz kernel 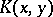defined on 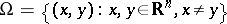with the following properties:

i) 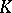is locally integrable on and satisfies ;

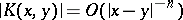ii) there exist constants 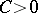and 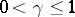such that for 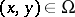and ,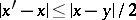

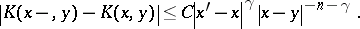Similarly, for 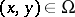and ,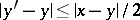

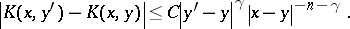iii) 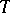can be extended to a bounded linear operator on .

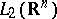This last condition is hard to verify in general. Thus, it is an important result, known as the 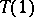-theorem, that if i) and ii) hold, then iii) is equivalent to: 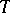is weakly bounded on 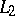and both 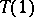and 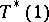are in 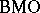, cf. [a3], [a11], [a12]. It is known that diagonal operators with respect to an orthonormal wavelet basis are of Calderón–Zygmund type. This connection with wavelet analysis is treated in [a11].

Many of the results concerning 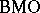-functions have been generalized to the setting of martingales, cf. [a9] (see also Martingale).

The duality result indicates that 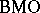plays a role in complex analysis as well. The class of holomorphic functions (cf. Analytic function) on a domain with boundary values in 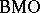is denoted by 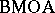, and is called the 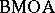-space, i.e., .

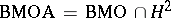Carleson's corona theorem [a5] for the disc states that for given bounded holomorphic functions 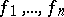such that 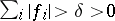there exist bounded holomorphic functions 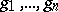such that 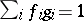. So far (1996), this result could not be extended to the unit ball in 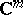, , 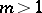but it can be proved if one only requires that 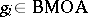, cf. [a13].

The definition of 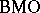makes sense as soon as there are proper notions of integral and ball in a space. Thus, 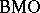can be defined in spaces of homogeneous type, cf. [a1], [a2], [a10]. In the setting of several complex variables, several types of 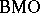-spaces arise on the boundary of (strictly) pseudoconvex domains, depending on whether one considers the isotropic Euclidean balls or the non-isotropic balls that are natural in connection with pseudo-convexity, cf. [a10].

References

[a1]	R.R. Coifman, G. Weiss, "Analyse harmonique non-commutative sur certains espaces homogènes" , Lecture Notes in Mathematics , 242 , Springer (1971)
[a2]	R.R. Coifman, G. Weiss, "Extensions of Hardy spaces and their use in analysis" Bull. Amer. Math. Soc. , 83 (1977) pp. 569–643
[a3]	G. David, J.-L. Journé, "A boundedness criterion for generalized Calderón–Zygmund operators" Ann. of Math. , 120 (1985) pp. 371–397
[a4]	J. Garcia-Cuervas, J.L. Rubio de Francia, "Weighted norm inequalities and related topics" , Math. Stud. , 116 , North-Holland (1985)
[a5]	J. Garnett, "Bounded analytic functions" , Acad. Press (1981)
[a6]	C. Fefferman, "Characterizations of bounded mean oscillation" Bull. Amer. Math. Soc. , 77 (1971) pp. 587–588
[a7]	C. Fefferman, E.M. Stein, "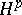 spaces of several variables" Acta Math. , 129 (1974) pp. 137–193
[a8]	F. John, L. Nirenberg, "On functions of bounded mean oscillation" Comm. Pure Appl. Math. , 14 (1961) pp. 415–426
[a9]	N. Kazamaki, "Continuous exponential martingales and BMO" , Lecture Notes in Mathematics , 579 , Springer (1994)
[a10]	S.G. Krantz, "Geometric analysis and function spaces" , CBMS , 81 , Amer. Math. Soc. (1993)
[a11]	Y. Meyer, "Ondelettes et opérateurs II. Opérateurs de Calderón–Zygmund" , Actual. Math. , Hermann (1990)
[a12]	E.M. Stein, "Harmonic analysis: real variable methods, orthogonality, and oscillatory integrals" , Math. Ser. , 43 , Princeton Univ. Press (1993)
[a13]	N.Th. Varopoulos, "BMO functions and the 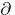equation" Pacific J. Math. , 71 (1977) pp. 221–272