Difference between revisions of "Automorphic form"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a0141601.png | ||
| + | $#A+1 = 14 n = 1 | ||
| + | $#C+1 = 14 : ~/encyclopedia/old_files/data/A014/A.0104160 Automorphic form | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Meromorphic function|meromorphic function]] on a bounded domain $ D $ | |
| + | of the complex space $ \mathbf C ^ {n} $ | ||
| + | that, for some [[Discrete group of transformations|discrete group of transformations]] $ \Gamma $ | ||
| + | operating on this domain, satisfies an equation: | ||
| − | + | $$ | |
| + | f ( \gamma ( x ) ) = j _ \gamma ^ {-m} ( x ) f ( x ) , | ||
| + | \ x \in D , \gamma \in \Gamma , | ||
| + | $$ | ||
| − | converges for large values of | + | Here $ j _ \gamma (x) $ |
| + | is the Jacobian of the mapping $ x \rightarrow \gamma (x) $ | ||
| + | and $ m $ | ||
| + | is an integer known as the weight of the automorphic form. If the group $ \Gamma $ | ||
| + | acts fixed-point free, then automorphic forms define differential forms on the quotient space $ D / \Gamma $ | ||
| + | and vice versa. Automorphic forms may be used in the construction of non-trivial automorphic functions (cf. [[Automorphic function|Automorphic function]]). It has been shown that if $ g(x) $ | ||
| + | is a function that is holomorphic and bounded on a domain $ D $, | ||
| + | then the series | ||
| + | |||
| + | $$ | ||
| + | \sum _ {\gamma \in \Gamma } | ||
| + | g( \gamma (x)) j _ \gamma ^ {m} (x) | ||
| + | $$ | ||
| + | |||
| + | converges for large values of $ m $, | ||
| + | thus representing a non-trivial automorphic function of weight $ m $. | ||
| + | These series are called Poincaré theta-series. | ||
The classical definition of automorphic forms, given above, has recently served as the starting point of a far-reaching generalization in the theory of discrete subgroups of Lie groups and adèle groups. | The classical definition of automorphic forms, given above, has recently served as the starting point of a far-reaching generalization in the theory of discrete subgroups of Lie groups and adèle groups. | ||
| Line 13: | Line 43: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Poincaré, , ''Oeuvres de H. Poincaré'' , Gauthier-Villars (1916–1965)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Poincaré, , ''Oeuvres de H. Poincaré'' , Gauthier-Villars (1916–1965)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 10:01, 25 April 2020
A meromorphic function on a bounded domain $ D $
of the complex space $ \mathbf C ^ {n} $
that, for some discrete group of transformations $ \Gamma $
operating on this domain, satisfies an equation:
$$ f ( \gamma ( x ) ) = j _ \gamma ^ {-m} ( x ) f ( x ) , \ x \in D , \gamma \in \Gamma , $$
Here $ j _ \gamma (x) $ is the Jacobian of the mapping $ x \rightarrow \gamma (x) $ and $ m $ is an integer known as the weight of the automorphic form. If the group $ \Gamma $ acts fixed-point free, then automorphic forms define differential forms on the quotient space $ D / \Gamma $ and vice versa. Automorphic forms may be used in the construction of non-trivial automorphic functions (cf. Automorphic function). It has been shown that if $ g(x) $ is a function that is holomorphic and bounded on a domain $ D $, then the series
$$ \sum _ {\gamma \in \Gamma } g( \gamma (x)) j _ \gamma ^ {m} (x) $$
converges for large values of $ m $, thus representing a non-trivial automorphic function of weight $ m $. These series are called Poincaré theta-series.
The classical definition of automorphic forms, given above, has recently served as the starting point of a far-reaching generalization in the theory of discrete subgroups of Lie groups and adèle groups.
References
| [1] | H. Poincaré, , Oeuvres de H. Poincaré , Gauthier-Villars (1916–1965) |
| [2] | C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955) |
Comments
References [a2] and [a3] can serve to get some idea of modern developments and topics in the theory of automorphic forms and its relations with other parts of mathematics. (Cf. the comments to the article Automorphic function for a more general notion).
References
| [a1] | W.L. Baily jr., "Introductory lectures on automorphic forms" , Iwanami Shoten & Princeton Univ. Press (1973) |
| [a2] | A. Borel (ed.) W. Casselman (ed.) , Automorphic forms, representations and 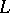 -functions , Proc. Symp. Pure Math. , 33:1–2 , Amer. Math. Soc. (1979) -functions , Proc. Symp. Pure Math. , 33:1–2 , Amer. Math. Soc. (1979) |
| [a3] | S.S. Gelbart, "Automorphic forms on adèle groups" , Princeton Univ. Press (1975) |
Automorphic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Automorphic_form&oldid=45527