Algebraic number theory
The branch of number theory with the basic aim of studying properties of algebraic integers in algebraic number fields 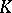 of finite degree over the field
of finite degree over the field 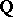 of rational numbers (cf. Algebraic number).
of rational numbers (cf. Algebraic number).
The set of algebraic integers 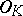 of a field
of a field 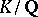 — an extension
— an extension 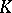 of
of 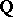 of degree
of degree  (cf. Extension of a field) — can be obtained from an integral basis
(cf. Extension of a field) — can be obtained from an integral basis 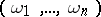 ; this means that each algebraic integer (i.e. element of
; this means that each algebraic integer (i.e. element of 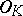 ) can be written in the form
) can be written in the form 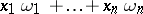 where all the
where all the 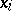 run through the rational integers (i.e.
run through the rational integers (i.e. 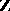 ). Moreover, such a representation is unique for each algebraic integer in
). Moreover, such a representation is unique for each algebraic integer in 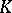 .
.
However, properties of rational integers often do not have obvious analogues for algebraic integers. The first such property is related to units, the invertible elements of 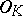 (cf. Unit). The field of rational numbers has only
(cf. Unit). The field of rational numbers has only 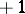 and
and 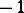 as units, but a general algebraic number field may contain an infinite number of units. E.g. consider the real quadratic field
as units, but a general algebraic number field may contain an infinite number of units. E.g. consider the real quadratic field 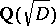 , where
, where 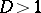 is a rational integer not equal to a square. If, moreover,
is a rational integer not equal to a square. If, moreover, 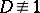
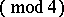 , then
, then 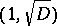 is an integral basis for it. The Pell equation
is an integral basis for it. The Pell equation 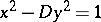 has an infinite number of solutions
has an infinite number of solutions 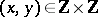 . Any of them gives rise to a unit
. Any of them gives rise to a unit  of
of 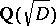 . In fact,
. In fact,
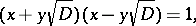 |
and
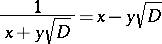 |
is also an algebraic integer in 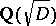 . The units of
. The units of 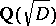 form an infinite multiplicative group (the group of Pell units). The question arises: What is the structure of this group?
form an infinite multiplicative group (the group of Pell units). The question arises: What is the structure of this group?
A second property of rational numbers without an obvious analogue for algebraic numbers is related to the theorem on unique factorization of rational integers  in prime factors:
in prime factors:
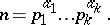 |
For algebraic numbers such a unique factorization need not hold. E.g. consider the field 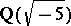 . In it, the number 6 has two essentially different factorizations:
. In it, the number 6 has two essentially different factorizations: 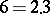 ,
, 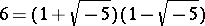 . For extensions of higher degree the situation becomes still more complicated. The question arises: What becomes of the unique factorization theorem, does it have a meaning at all in algebraic number fields?
. For extensions of higher degree the situation becomes still more complicated. The question arises: What becomes of the unique factorization theorem, does it have a meaning at all in algebraic number fields?
A third property without an obvious analogue is related to prime numbers. An ordinary prime number need not remain a prime number in an algebraic number field. E.g. in the field 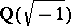 of Gaussian numbers the prime number 5 has a factorization:
of Gaussian numbers the prime number 5 has a factorization: 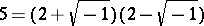 . However, the prime number 7 remains prime in this field. The question arises: Do there exist general laws governing the behaviour of prime numbers in algebraic number fields of higher degree? In other words, is it possible to find rules that would give a definite answer to the following question: Does a given prime number remain prime in a field
. However, the prime number 7 remains prime in this field. The question arises: Do there exist general laws governing the behaviour of prime numbers in algebraic number fields of higher degree? In other words, is it possible to find rules that would give a definite answer to the following question: Does a given prime number remain prime in a field 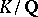 or does it split in it, and if it splits, in how many factors?
or does it split in it, and if it splits, in how many factors?
Finally, a last (fourth) problem concerns the general structure of algebraic number fields. The field  is the minimal field of characteristic zero without proper subfields. Any other algebraic number field does have subfields. E.g.,
is the minimal field of characteristic zero without proper subfields. Any other algebraic number field does have subfields. E.g.,  is a subfield of any algebraic number field. The question arises: How many subfields are contained in a given extension
is a subfield of any algebraic number field. The question arises: How many subfields are contained in a given extension  , finitely or infinitely many, and what is their structure?
, finitely or infinitely many, and what is their structure?
These are four main problems in algebraic number theory, and answering them constitutes the content of algebraic number theory. It is quite natural to start with the fourth problem, since its answer will shed light on the other three. The problem was solved by E. Galois in the 1820s (cf. Galois theory). The fact that the number of subfields of an extension 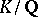 of degree
of degree  over
over 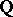 is finite follows from the existence of a one-to-one correspondence (the fundamental Galois correspondence) between all subfields of the normal closure of
is finite follows from the existence of a one-to-one correspondence (the fundamental Galois correspondence) between all subfields of the normal closure of 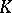 (cf. Normal extension) and the subgroups of its Galois group, a finite group of finite order (number of elements) at most
(cf. Normal extension) and the subgroups of its Galois group, a finite group of finite order (number of elements) at most  .
.
The structure of the group of units of a field was elucidated by P. Dirichlet. His basic idea can be given by taking the group of Pell units (cf. above) as example. Any power of such a unit (both positive or negative) is a unit. There is a fundamental unit 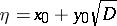 , and all other units are plus or minus integral powers of it; hence, the Pell units form the product of
, and all other units are plus or minus integral powers of it; hence, the Pell units form the product of 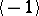 with an infinite cyclic group. This fact is a special case of the general Dirichlet unit theorem for algebraic number fields: If the degree of a field
with an infinite cyclic group. This fact is a special case of the general Dirichlet unit theorem for algebraic number fields: If the degree of a field 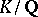 is
is 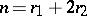 , where
, where  is the number of real imbeddings
is the number of real imbeddings 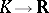 and
and 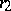 the number of complex-conjugate pairs of complex imbeddings
the number of complex-conjugate pairs of complex imbeddings 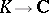 , then the group of units
, then the group of units 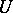 of
of 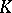 is the product of a finite cyclic group
is the product of a finite cyclic group 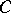 and
and  infinite cyclic groups:
infinite cyclic groups:
 |
Here  are independent fundamental units and
are independent fundamental units and  is the group of roots of unity contained in
is the group of roots of unity contained in 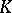 . The norm of any unit in a field, i.e. the product of the unit by its conjugates, is equal to
. The norm of any unit in a field, i.e. the product of the unit by its conjugates, is equal to 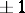 .
.
The problem of the non-unique factorization of algebraic integers in algebraic number fields was solved by E. Kummer, who started from a special case; he tried to solve Fermat's last theorem on the impossibility of solving the equation 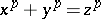 in non-zero integers for any prime number
in non-zero integers for any prime number  . Kummer expanded the left-hand side using
. Kummer expanded the left-hand side using 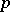 -th roots of unity, and hence the problem was reduced to one about the algebraic integers of
-th roots of unity, and hence the problem was reduced to one about the algebraic integers of 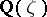 ,
, 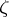 a primitive
a primitive 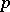 -th root of unity. If there would be unique factorization into prime factors in
-th root of unity. If there would be unique factorization into prime factors in 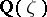 , then it would have been sufficient to prove that not all prime factors at the left-hand side occur with an exponent that is a multiple of
, then it would have been sufficient to prove that not all prime factors at the left-hand side occur with an exponent that is a multiple of 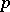 . This was Kummer's first point of view, but Dirichlet pointed out to him that unique factorization need not hold. In order to overcome this difficulty Kummer introduced ideal numbers, thus altering the entire structure of algebraic number theory for the future. The concept of an ideal number arises from the fact that if a field
. This was Kummer's first point of view, but Dirichlet pointed out to him that unique factorization need not hold. In order to overcome this difficulty Kummer introduced ideal numbers, thus altering the entire structure of algebraic number theory for the future. The concept of an ideal number arises from the fact that if a field 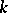 does not contain prime numbers into which any algebraic integer in
does not contain prime numbers into which any algebraic integer in 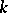 can be split, then there is a field
can be split, then there is a field 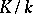 of finite degree over
of finite degree over 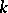 in which there does exist a collection of numbers that play the role of primes for
in which there does exist a collection of numbers that play the role of primes for 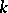 . These numbers were called ideal by Kummer (since they do not lie in the original field
. These numbers were called ideal by Kummer (since they do not lie in the original field 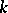 ). By introducing ideal numbers the theorem on unique factorization in
). By introducing ideal numbers the theorem on unique factorization in 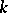 holds. Two numbers in a field that differ by a unit (so-called associated numbers) have one and the same ideal factors. (Note that ideal numbers are defined relative to the original field
holds. Two numbers in a field that differ by a unit (so-called associated numbers) have one and the same ideal factors. (Note that ideal numbers are defined relative to the original field 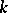 ; for another field
; for another field 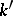 one must construct an extension
one must construct an extension 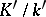 (of possibly different degree over
(of possibly different degree over 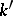 ) in which all ideal numbers of
) in which all ideal numbers of  are contained.)
are contained.)
Kummer also introduced the concept of the ideal class number of a field 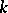 . Two ideal numbers are said to belong to the same class if their quotient belongs to
. Two ideal numbers are said to belong to the same class if their quotient belongs to  . The number of classes thus obtained is called the ideal class number of
. The number of classes thus obtained is called the ideal class number of 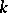 . He obtained the following important result: The class number
. He obtained the following important result: The class number 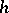 of
of 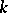 is finite, and the classes form an Abelian group under multiplication. Thus, any ideal number can be regarded as the
is finite, and the classes form an Abelian group under multiplication. Thus, any ideal number can be regarded as the 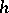 -th root of some element of the original field
-th root of some element of the original field 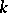 . The class number can be explicitly described in terms of other field constants (the regulator, the discriminant and the degree of the field).
. The class number can be explicitly described in terms of other field constants (the regulator, the discriminant and the degree of the field).
Subsequently, the concept of an ideal number was replaced by that of an ideal, equivalent to it, which can be described in terms of the field 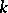 itself. Already in the 1950s the concept of an ideal was generalized to the more comprehensive concept of a divisor. Therefore, the modern theory of Kummer may be stated in terms of divisors. For algebraic number fields, however, the concepts of a divisor and an ideal coincide, and such fields only will be considered in the sequel. The concept of an ideal is related to that of non-associated numbers, which helps in understanding the deep connections between Kummer's theory and Dirichlet's theory of units. Although Kummer did not succeed in solving Fermat's problem, his ideas extended far beyond this problem and the concept of an ideal has now become fundamental in many branches of mathematics.
itself. Already in the 1950s the concept of an ideal was generalized to the more comprehensive concept of a divisor. Therefore, the modern theory of Kummer may be stated in terms of divisors. For algebraic number fields, however, the concepts of a divisor and an ideal coincide, and such fields only will be considered in the sequel. The concept of an ideal is related to that of non-associated numbers, which helps in understanding the deep connections between Kummer's theory and Dirichlet's theory of units. Although Kummer did not succeed in solving Fermat's problem, his ideas extended far beyond this problem and the concept of an ideal has now become fundamental in many branches of mathematics.
Since prime ideal numbers are defined relative to a field or, in modern terminology, since they are prime ideals in a field, the third problem on the factorization of ordinary prime numbers in an algebraic number field can be stated in the following general form. Suppose one is given a field  and a prime ideal
and a prime ideal 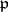 of its ring of algebraic integers. The question is: Does
of its ring of algebraic integers. The question is: Does  remain prime in an extension
remain prime in an extension 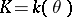 or does it split in a product of prime ideals of the ring of algebraic integers of
or does it split in a product of prime ideals of the ring of algebraic integers of 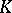 ? In the latter case: By which law does it split? This question led to class field theory, a central part of modern algebraic number theory. The first solution of this problem was given by Kummer, who proved that if
? In the latter case: By which law does it split? This question led to class field theory, a central part of modern algebraic number theory. The first solution of this problem was given by Kummer, who proved that if 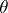 is a root of an irreducible polynomial
is a root of an irreducible polynomial 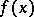 and
and 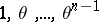 is an integral basis for
is an integral basis for 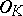 over
over 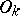 , then
, then 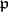 splits in
splits in 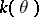 "by the same law as fx" does in the residue field (
"by the same law as fx" does in the residue field (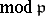 ). In other words, the factorization of
). In other words, the factorization of 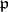 in
in 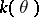 is determined by the congruence
is determined by the congruence
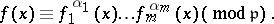 |
The corresponding factorization is called Kummer's formula (or Kummer's decomposition)
 | (1) |
where 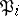 are prime ideals in
are prime ideals in 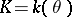 .
.
In principle, this equation solves the third problem in algebraic number theory, but it is a local equation in the sense that it is necessary to check it for each prime ideal separately. The problem of partitioning the set of all prime ideals in classes such that the factorization law is the same in any given class and such that, moreover, it is possible to give a simple description of these classes, is solved by class field theory for extensions 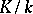 with Abelian Galois group
with Abelian Galois group 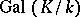 .
.
Equation (1) yields a preliminary concept of a class. Let  be the degree of the extension
be the degree of the extension 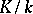 and let
and let 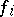 be the relative degree of the ideal
be the relative degree of the ideal 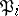 . Computing the relative norms
. Computing the relative norms 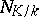 of both parts of (1) leads to
of both parts of (1) leads to
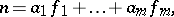 | (2) |
in which 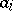 and
and 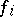 are natural numbers. For
are natural numbers. For  fixed equation (2) has a finite number of solutions, so that the set of all prime ideals of
fixed equation (2) has a finite number of solutions, so that the set of all prime ideals of 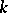 can be partitioned into a finite number of classes and one can collect the prime ideals whose Kummer decomposition corresponds to one solution
can be partitioned into a finite number of classes and one can collect the prime ideals whose Kummer decomposition corresponds to one solution 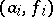 of (2) into one class. The number of prime ideals with the property that some
of (2) into one class. The number of prime ideals with the property that some 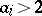 , is finite, and they all are divisors of the discriminant
, is finite, and they all are divisors of the discriminant 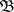 of
of 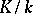 . Only infinite classes are of interest, so that classes for which
. Only infinite classes are of interest, so that classes for which 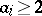 can be ignored.
can be ignored.
In order to simplify the exposition, the field 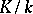 is considered to be normal from now on. In such fields the condition
is considered to be normal from now on. In such fields the condition
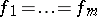 |
holds. Therefore, the set of all 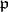 not dividing
not dividing 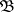 is partitioned into
is partitioned into 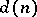 classes, where
classes, where 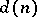 denotes the number of divisors. The class with
denotes the number of divisors. The class with  is of special interest, in it
is of special interest, in it
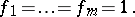 |
A prime ideal 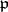 in it has maximal number of prime divisors in
in it has maximal number of prime divisors in 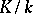 :
:
 | (3) |
Such 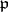 are said to split completely (or to be totally split), and their class is called the principal class of
are said to split completely (or to be totally split), and their class is called the principal class of 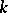 relative to
relative to 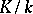 . It is a principal object of study in class field theory. In order to be able to define the principal class via (3) it is necessary to give a proof of the facts that prime ideals satisfying (1) do exist in
. It is a principal object of study in class field theory. In order to be able to define the principal class via (3) it is necessary to give a proof of the facts that prime ideals satisfying (1) do exist in  and that there are infinitely many such ideals. Therefore a basic problem in class field theory is to define the principal class in terms of the field
and that there are infinitely many such ideals. Therefore a basic problem in class field theory is to define the principal class in terms of the field 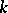 itself in such a way that its infinite nature would follow. This problem has been completely solved for Abelian extensions
itself in such a way that its infinite nature would follow. This problem has been completely solved for Abelian extensions 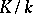 .
.
In order to be able to understand the ideas of class field theory better, it is necessary to introduce the general concept of an ideal class group. Kummer's definition given above then corresponds to the modern concept of an absolute ideal class group. The general concept of an ideal class group which is used nowadays is due to H. Weber and T. Takagi, [5].
Weber introduced the concept of the conductor of a class group. Let 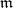 be an integral ideal of
be an integral ideal of 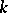 , let
, let 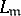 be the subgroup of principal ideals
be the subgroup of principal ideals 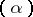 of
of 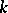 given by
given by 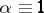
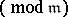 and let
and let 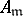 be the subgroup of all ideals of
be the subgroup of all ideals of 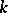 that are relatively prime with
that are relatively prime with  . A subgroup
. A subgroup 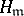 satisfying
satisfying  can be regarded as a group of principal ideals, and a (generalized) class group
can be regarded as a group of principal ideals, and a (generalized) class group 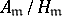 is constructed in this way. For
is constructed in this way. For 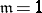 and
and  one obtains Kummer's definition. In the general case
one obtains Kummer's definition. In the general case 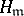 consists of progressions
consists of progressions 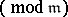 whose residue classes form a subgroup of the whole multiplicative group
whose residue classes form a subgroup of the whole multiplicative group 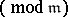 . The order
. The order 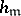 of this generalized class group satisfies the estimates
of this generalized class group satisfies the estimates 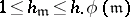 , where
, where 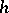 is the order of the absolute class group and
is the order of the absolute class group and 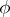 is Euler's phi-function. For different conductors
is Euler's phi-function. For different conductors 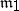 and
and 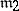 the class groups may be equivalent if
the class groups may be equivalent if 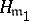 and
and 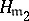 consists in fact of the same progressions
consists in fact of the same progressions 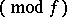 , where
, where  . If one agrees not to distinguish between equivalent class groups, then one obtains the concept of a class group according to Weber with a conductor
. If one agrees not to distinguish between equivalent class groups, then one obtains the concept of a class group according to Weber with a conductor 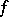 that is the greatest common divisor of all equivalent conductors. A class field according to Weber is a field
that is the greatest common divisor of all equivalent conductors. A class field according to Weber is a field 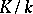 in which only the prime ideals in its principal class
in which only the prime ideals in its principal class 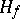 , and only these, split completely. Dirichlet's theorem on prime ideals in progressions, which is valid in every field
, and only these, split completely. Dirichlet's theorem on prime ideals in progressions, which is valid in every field 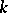 , implies that there are infinitely many prime ideals. Weber has shown that in certain particular cases the Galois group
, implies that there are infinitely many prime ideals. Weber has shown that in certain particular cases the Galois group 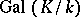 of a class field and the class group
of a class field and the class group 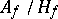 of
of 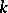 are isomorphic.
are isomorphic.
A new point of view on class field theory, which is still valid, originated with D. Hilbert. He understood that between all relatively Abelian extensions of a field 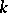 and all class fields for this field there must exist a one-to-one correspondence. This correspondence can be stated as follows. If for some conductor
and all class fields for this field there must exist a one-to-one correspondence. This correspondence can be stated as follows. If for some conductor 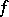 one constructs the Weber class group, then there is only one normal extension
one constructs the Weber class group, then there is only one normal extension 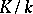 in which the prime ideals of Weber's principal class, and only these, will split completely. Moreover, the Galois group of
in which the prime ideals of Weber's principal class, and only these, will split completely. Moreover, the Galois group of 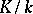 is isomorphic to the Weber class group and the discriminant
is isomorphic to the Weber class group and the discriminant 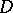 of
of 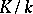 consists of the same prime ideals as the conductor
consists of the same prime ideals as the conductor 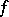 . The converse is also true: If an Abelian extension with Galois group
. The converse is also true: If an Abelian extension with Galois group 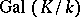 is given, then there exists a method (subsequently explicitly formulated by Takagi) by which one can uniquely construct a principal class
is given, then there exists a method (subsequently explicitly formulated by Takagi) by which one can uniquely construct a principal class 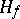 such that the class group
such that the class group 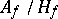 is isomorphic to
is isomorphic to 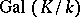 , only the prime ideals of
, only the prime ideals of 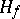 split completely in
split completely in 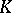 , and such that the conductor
, and such that the conductor 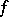 has the same prime divisors as the discriminant
has the same prime divisors as the discriminant 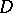 of
of 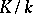 . The "duality" was stated by Hilbert in 1900 as a hypothesis (he proved it only in special cases). In its general form it was proved by Takagi.
. The "duality" was stated by Hilbert in 1900 as a hypothesis (he proved it only in special cases). In its general form it was proved by Takagi.
The next important stage of development of class group theory is related to the name of E. Artin, who revealed the special role of the canonical isomorphism between the Galois group and the ideal class group. He proved that this isomorphism is given by the Frobenius automorphism 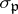 of an Abelian extension
of an Abelian extension 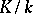 , defined as
, defined as
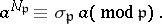 |
Here 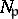 is the absolute norm of the ideal
is the absolute norm of the ideal 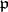 ,
,  runs through all numbers of
runs through all numbers of  and
and 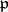 is a prime ideal of
is a prime ideal of 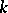 . The automorphism
. The automorphism 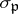 (nowadays denoted by
(nowadays denoted by
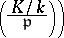 |
depends (in an appropriate group) only on the ideal class to which 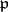 belongs. It is multiplicative:
belongs. It is multiplicative:
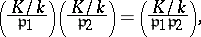 |
where the symbol at the right-hand side is understood as an automorphism of the class to which 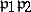 belongs. With this in mind, Artin introduced the symbol
belongs. With this in mind, Artin introduced the symbol
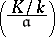 |
on the entire group 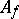 of ideals
of ideals  of
of 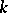 that are relatively prime with the conductor
that are relatively prime with the conductor 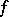 . It is called the Artin symbol and realizes an isomorphism between the class group
. It is called the Artin symbol and realizes an isomorphism between the class group 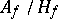 and the Galois group
and the Galois group 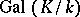 , whose explicit from is expressed in Artin's reciprocity law:
, whose explicit from is expressed in Artin's reciprocity law:
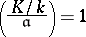 |
if and only if 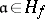 (reciprocity as a correspondence between the groups
(reciprocity as a correspondence between the groups 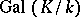 and
and 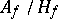 ). From this one can obtain the classical form of the reciprocity law in the language of Kummer's power reciprocity symbol (one has to consider the field
). From this one can obtain the classical form of the reciprocity law in the language of Kummer's power reciprocity symbol (one has to consider the field 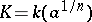 , cf. Reciprocity laws). This form, in turn, implies the reciprocity law for Hilbert's symbol. In all three forms the reciprocity law is regarded as an isomorphism of groups, and the symbols of Artin, Kummer and Hilbert are regarded as group elements realizing this isomorphism. However, each of them also has a numerical value, which is equal to some
, cf. Reciprocity laws). This form, in turn, implies the reciprocity law for Hilbert's symbol. In all three forms the reciprocity law is regarded as an isomorphism of groups, and the symbols of Artin, Kummer and Hilbert are regarded as group elements realizing this isomorphism. However, each of them also has a numerical value, which is equal to some  -th root of unity. Therefore one can formulate the reciprocity law as follows. Given the value of
-th root of unity. Therefore one can formulate the reciprocity law as follows. Given the value of 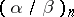 , it is required to find the value of the symbol
, it is required to find the value of the symbol  reciprocal to it, i.e. to exhibit the explicit form of the function of
reciprocal to it, i.e. to exhibit the explicit form of the function of 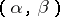 defined by
defined by
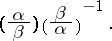 |
In this form the law first appeared in the work of C.F. Gauss (cf. Gauss reciprocity law) for quadratic fields and in the work of Kummer for cyclotomic fields of prime degree. The study of the reciprocity law in this form was subsequently continued by C.G.J. Jacobi, F.G.M. Eisenstein, Hilbert, H. Hasse, and others, but they only obtained partial results. I.R. Shafarevich [6] solved this problem in its general form in 1948, basing himself on the idea of establishing a connection between the arithmetic definition of the symbol
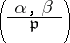 |
and the analytic definition of an Abelian differential 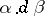 on a Riemann surface. He gave a construction of
on a Riemann surface. He gave a construction of
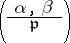 |
which precisely corresponds to the determination of the residue of 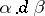 in the
in the 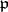 -adic field. For this purpose he introduced
-adic field. For this purpose he introduced 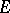 -functions, also called Shafarevich functions, in terms of which he also obtained an explicit form of the reciprocity law in the general case.
-functions, also called Shafarevich functions, in terms of which he also obtained an explicit form of the reciprocity law in the general case.
In the late 1920s Hasse introduced the idea of doing class field theory for one prime ideal of 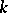 at a time, and reformulated and proved many theorems for an Abelian extension
at a time, and reformulated and proved many theorems for an Abelian extension 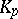 of a local field
of a local field 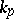 . At first the idea was of secondary importance only (the results were obtained as a consequence of the local theory), but at the end of the 1930s C. Chevalley proved the extraordinary importance of the local point of view in the creation of class field theory. He introduced the concept of an idèle group and formulated general class field theory from the local point of view. Following this the local-global principle became established in class field theory. Subsequently it was extended and refined (cf. [5]), and as a result Abelian class field theory took a structured and completed form. The problem of creating non-Abelian class field theory for normal extensions with non-Abelian Galois group remains.
. At first the idea was of secondary importance only (the results were obtained as a consequence of the local theory), but at the end of the 1930s C. Chevalley proved the extraordinary importance of the local point of view in the creation of class field theory. He introduced the concept of an idèle group and formulated general class field theory from the local point of view. Following this the local-global principle became established in class field theory. Subsequently it was extended and refined (cf. [5]), and as a result Abelian class field theory took a structured and completed form. The problem of creating non-Abelian class field theory for normal extensions with non-Abelian Galois group remains.
The exposition above relates mainly to the qualitative aspects of algebraic number theory. In questions of quantitative estimation and methods algebraic number theory is intimately connected with analytic number theory. It is also based, to a large extent, on properties of 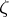 -functions and
-functions and 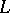 -functions of algebraic fields.
-functions of algebraic fields.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | M.M. Postnikov, "Fundamentals of Galois theory" , Noordhoff (1962) (Translated from Russian) |
| [3] | H. Weyl, "Algebraic theory of numbers" , Princeton Univ. Press (1959) |
| [4] | S. Lang, "Algebraic number theory" , Addison-Wesley (1970) |
| [5] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) |
| [6] | I.R. Shafarevich, "General reciprocity laws" Mat. Sb. , 26 (68) : 1 (1950) pp. 113–146 (In Russian) |
| [7] | "Hilbert's problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 437–479 (Translated from German) |
| [8] | E. Artin, J. Tate, "Class field theory" , Benjamin (1967) |
| [9] | A. Weil, "Basic number theory" , Springer (1974) |
| [10] | S. Lang, "Algebraic numbers" , Addison-Wesley (1964) |
| [11] | N. Bourbaki, "Commutative algebra" , Addison-Wesley (1966) (Translated from French) |
Comments
An algebraic number field of degree  is a degree
is a degree  extension of the field
extension of the field 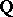 of rational numbers. An element
of rational numbers. An element 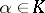 is an algebraic integer if it is integral over
is an algebraic integer if it is integral over 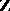 , i.e. if it is a root of a monic polynomial in
, i.e. if it is a root of a monic polynomial in 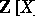 . These form a free Abelian subgroup of rank
. These form a free Abelian subgroup of rank  , called the ring of integers
, called the ring of integers 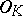 of
of 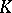 and also the principal order of
and also the principal order of 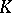 ; a basis of
; a basis of 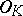 is an integral basis, also called a minimal basis.
is an integral basis, also called a minimal basis.
For Kummer's approach to the Fermat problem cf. [a3]. The link (equivalence) between Kummer's ideal numbers and ideals comes from the fact that for the prime ideals in 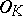 there is a field extension
there is a field extension 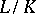 in which they become principal ideals.
in which they become principal ideals.
The relative degree  of an ideal
of an ideal 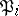 is the degree of the residue field extension
is the degree of the residue field extension 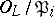 over
over 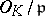 where
where 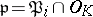 .
.
For more details, definitions, newer results, and more precise statements of much of the above cf. various more specified articles in this Encyclopaedia. In particular the articles Algebraic number; Unit; Extension of a field; Regulator of an algebraic number field; Discriminant; Frobenius automorphism (also for Artin symbol), Kummer theorem on decomposition of ideals, and especially class field theory.
The ideal class groups 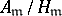 are also often known as ray class groups
are also often known as ray class groups 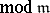 , and the corresponding fields as ray class fields. The class field corresponding to the ray class group
, and the corresponding fields as ray class fields. The class field corresponding to the ray class group 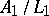 is the Hilbert class field. The definitions above ignore some problems with the Archimedean primes; in particular the principal ideals
is the Hilbert class field. The definitions above ignore some problems with the Archimedean primes; in particular the principal ideals 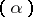 making up
making up 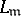 must have
must have 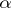 totally positive, i.e. such that all real conjugates of
totally positive, i.e. such that all real conjugates of 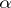 are
are 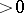 .
.
The discussion of class field theory above (up to the mention of idèles) is in terms of the older ideal-theoretic formulation as in e.g. Hasse's Zahlbericht [a1], which in fact can be advantageously consulted for more details and precise statements. For a discussion of the relations between the ideal-theoretic formulations and the modern idèle based class field theory [a2] is recommended.
References
| [a1] | H. Hasse, "Bericht über neuere Untersuchungen und Probleme aus der Theorie der algebraïsche Zahlkörper" , I.II , Physika Verlag (1965) |
| [a2] | J. Neukirch, "Class field theory" , Springer (1986) pp. Chapt. 4, Sect. 8 |
| [a3] | H. Pollard, "The theory of algebraic numbers" , Math. Assoc. Amer. (1950) |
| [a4] | E. Weiss, "Algebraic number theory" , McGraw-Hill (1963) pp. Sects. 4–9 |
Algebraic number theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_number_theory&oldid=12866