Adjoint action
of a Lie group
The linear action on the Lie algebra 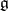 of the Lie group
of the Lie group 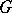 , denoted by
, denoted by 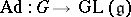 , that is defined as follows: Each element
, that is defined as follows: Each element 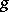 of
of 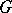 induces an inner automorphism of the Lie group
induces an inner automorphism of the Lie group  by the formula
by the formula 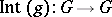 ,
, 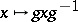 . Its differential,
. Its differential, 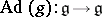 , gives an automorphism of the Lie algebra
, gives an automorphism of the Lie algebra 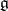 . The resulting linear representation
. The resulting linear representation 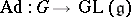 is called the adjoint representation of
is called the adjoint representation of 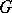 (cf. also Adjoint representation of a Lie group).
(cf. also Adjoint representation of a Lie group).
The kernel of the adjoint representation, 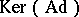 , contains the centre
, contains the centre 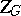 of
of 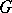 (cf. also Centre of a group), and coincides with
(cf. also Centre of a group), and coincides with 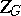 if
if 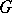 is connected. The image
is connected. The image 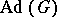 is called the adjoint group; it is a Lie subgroup of
is called the adjoint group; it is a Lie subgroup of 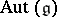 , the group of all automorphisms of the Lie algebra
, the group of all automorphisms of the Lie algebra 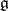 .
.
The differential of the adjoint representation 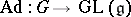 gives rise to a linear representation
gives rise to a linear representation 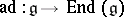 of the Lie algebra
of the Lie algebra  (cf. also Representation of a Lie algebra). It is given by the formula
(cf. also Representation of a Lie algebra). It is given by the formula
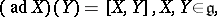 |
and is called the adjoint representation of 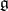 (cf. also Adjoint representation of a Lie group). The kernel,
(cf. also Adjoint representation of a Lie group). The kernel, 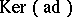 , coincides with the centre of the Lie algebra
, coincides with the centre of the Lie algebra 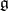 . The image,
. The image, 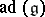 , forms a subalgebra of
, forms a subalgebra of 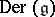 , the Lie algebra of all derivations of
, the Lie algebra of all derivations of  (cf. Derivation in a ring). If
(cf. Derivation in a ring). If 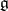 is a semi-simple Lie algebra (see Lie algebra, semi-simple), then
is a semi-simple Lie algebra (see Lie algebra, semi-simple), then  and
and  . An opposite extremal case is when
. An opposite extremal case is when 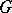 is Abelian; in this case
is Abelian; in this case 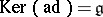 and
and  .
.
If 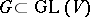 is a linear group acting on a vector space
is a linear group acting on a vector space 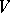 , then one can regard
, then one can regard 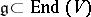 and the adjoint representation can be written in terms of matrix computation:
and the adjoint representation can be written in terms of matrix computation:
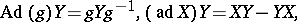 |
 |
The adjoint orbit through 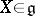 (see Orbit) is defined to be
(see Orbit) is defined to be  ; it is a submanifold of
; it is a submanifold of  .
.
Adjoint orbits for reductive Lie groups 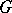 have been particularly studied. The adjoint orbit
have been particularly studied. The adjoint orbit 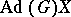 is called a semi-simple orbit (respectively, a nilpotent orbit) if
is called a semi-simple orbit (respectively, a nilpotent orbit) if 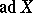 is a semi-simple (respectively, nilpotent) endomorphism of
is a semi-simple (respectively, nilpotent) endomorphism of 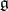 . The set
. The set
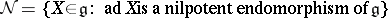 |
is an algebraic variety in 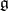 , called the nilpotent variety. It is the union of a finite number of nilpotent orbits. On the other hand,
, called the nilpotent variety. It is the union of a finite number of nilpotent orbits. On the other hand, 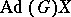 is a closed set in
is a closed set in  if and only if it is a semi-simple orbit. A semi-simple orbit
if and only if it is a semi-simple orbit. A semi-simple orbit  is called an elliptic orbit (respectively, a hyperbolic orbit) if all eigenvalues of
is called an elliptic orbit (respectively, a hyperbolic orbit) if all eigenvalues of 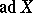 are purely imaginary (respectively, real). Any elliptic orbit carries a
are purely imaginary (respectively, real). Any elliptic orbit carries a  -invariant complex structure, while any hyperbolic obit carries a
-invariant complex structure, while any hyperbolic obit carries a  -invariant paracomplex structure.
-invariant paracomplex structure.
If 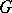 is compact, then all adjoint orbits are elliptic. For example, if
is compact, then all adjoint orbits are elliptic. For example, if  (a unitary group), then each adjoint orbit is biholomorphic to a generalized flag variety
(a unitary group), then each adjoint orbit is biholomorphic to a generalized flag variety 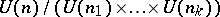 , for some partition
, for some partition 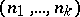 of
of  , and vice versa (cf. also Flag space; Algebraic variety).
, and vice versa (cf. also Flag space; Algebraic variety).
One writes  for the set of all adjoint orbits. The classical theory of the Jordan normal form of matrices (as well as the theory of other normal forms of matrices; cf. also Normal form) can be interpreted as the classification of
for the set of all adjoint orbits. The classical theory of the Jordan normal form of matrices (as well as the theory of other normal forms of matrices; cf. also Normal form) can be interpreted as the classification of 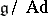 , for
, for 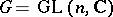 . If
. If 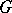 is a connected compact Lie group, then
is a connected compact Lie group, then 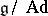 is bijective to
is bijective to  , the set of all orbits in
, the set of all orbits in  of the Weyl group
of the Weyl group 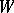 , where
, where  is a maximal Abelian subspace of
is a maximal Abelian subspace of 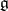 . This reduction is important in the Cartan–Weyl theory of the classification of irreducible representations, as well as their characters, for a compact Lie group (cf. also Lie group, compact; Irreducible representation).
. This reduction is important in the Cartan–Weyl theory of the classification of irreducible representations, as well as their characters, for a compact Lie group (cf. also Lie group, compact; Irreducible representation).
Bi-invariant tensors on a Lie group 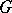 can be described in terms of invariants under the adjoint action. For example, the left-invariant measure on a connected Lie group
can be described in terms of invariants under the adjoint action. For example, the left-invariant measure on a connected Lie group 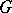 is also right invariant if and only if
is also right invariant if and only if 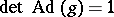 for any
for any 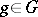 . Such a Lie group is called unimodular (cf. Haar measure). This is the case if
. Such a Lie group is called unimodular (cf. Haar measure). This is the case if 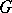 is nilpotent or reductive.
is nilpotent or reductive.
Let 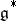 be the dual vector space of
be the dual vector space of  . The contragredient representation
. The contragredient representation  of the adjoint representation
of the adjoint representation 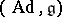 is called the co-adjoint representation. There is a close connection between irreducible unitary representations of
is called the co-adjoint representation. There is a close connection between irreducible unitary representations of 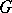 and co-adjoint orbits (see Orbit method).
and co-adjoint orbits (see Orbit method).
References
| [a1] | N. Bourbaki, "Elements of mathematics, Lie groups and Lie algebras" , Addison-Wesley (1975) pp. Chap. 2–3 (Translated from French) |
| [a2] | "Théorie des algèbres de Lie. Topologie des groupes de Lie" , Sém. Sophus Lie de l'Ecole Norm. Sup. 1954/55 , Secr. Math. Paris (1955) (0) |
| [a3] | T. Kobayashi, "Harmonic analysis on homogeneous manifolds of reductive type and unitary representation theory" , Transl. Ser. II , 183 , Amer. Math. Soc. (1998) pp. 1–31 |
| [a4] | F. Warner, "Foundations of differentiable manifolds and Lie groups" , Springer (1983) |
| [a5] | G. Warner, "Harmonic analysis on semisimple Lie groups I" , Springer (1972) |
Adjoint action. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_action&oldid=11210