Abundant number
Let  denote the sum of the distinct divisors of an integer
denote the sum of the distinct divisors of an integer  (cf. Divisor; Number of divisors). The integer
(cf. Divisor; Number of divisors). The integer  is called abundant if
is called abundant if  ; deficient if
; deficient if  ; and perfect if
; and perfect if  (cf. also Perfect number). Note that some authors call a number
(cf. also Perfect number). Note that some authors call a number  abundant if
abundant if  . Clearly, these numbers are in fact perfect or abundant (i.e. "non-deficient" ) numbers.
. Clearly, these numbers are in fact perfect or abundant (i.e. "non-deficient" ) numbers.
In [a5], L.E. Dickson gives details on the early history of abundant numbers. G. Nicomachus (about 100) separated the even numbers into abundant, deficient and perfect, and dwelled on the ethical importance of the three types. A.M.S. Boethius (around 500), in a Latin exposition of the arithmetic of Nicomachus, stated that perfect numbers are rare, while abundant ( "superfluous" ) and deficient ( "diminutos" ) numbers are found to an unlimited extent. N. Jordanus (around 1236) stated that every multiple of a perfect or abundant number is abundant. He attempted to prove the erroneous statement that all abundant numbers are even. C. Bovillus (around 1509) corrected this statement, by citing  and its multiples. Bachet de Méziriac (around 1600) gave a proof that
and its multiples. Bachet de Méziriac (around 1600) gave a proof that 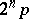 is perfect if
is perfect if 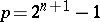 is a prime number, and abundant if
is a prime number, and abundant if  is composite. He remarked that the odd number
is composite. He remarked that the odd number 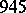 is abundant. J. Broscius (around 1652) showed that there are only
is abundant. J. Broscius (around 1652) showed that there are only 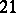 abundant numbers between
abundant numbers between 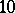 and
and 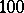 and all of them are even; the only odd abundant number less than
and all of them are even; the only odd abundant number less than 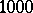 is
is 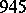 . (The statement by E. Lucas (1891) that
. (The statement by E. Lucas (1891) that 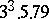 is the smallest odd abundant number is probably a misprint for
is the smallest odd abundant number is probably a misprint for 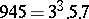 .) Ch. de Neuveglise (1700) proved that the products
.) Ch. de Neuveglise (1700) proved that the products 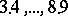 of two consecutive numbers are abundant, and all multiplies of
of two consecutive numbers are abundant, and all multiplies of 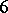 or an abundant number are abundant. J. Struve (1808) considered abundant numbers which are products
or an abundant number are abundant. J. Struve (1808) considered abundant numbers which are products 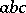 of three distinct prime numbers in ascending order; for
of three distinct prime numbers in ascending order; for  ,
, 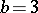 ,
, 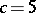 or
or 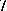 , and for
, and for 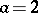 ,
, 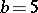 ,
, 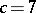 ,
,  is abundant for any prime number
is abundant for any prime number 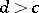 . Of the numbers
. Of the numbers 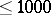 ,
, 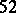 are abundant.
are abundant.
Dickson (1913, [a6]) called a non-deficient number primitive abundant if it is not a multiple of a smaller non-deficient number. He proved that there are only a finite number of primitive non-deficient numbers having a given number of distinct odd prime factors and a given number of factors  .
.
There is no odd abundant number with fewer than three distinct prime factors, the primitive ones with three are
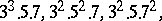 |
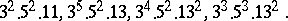 |
He gave also a table of all even abundant numbers 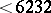 . Dickson's result was a starting point for much further research. In 1949 and 1968, H.N. Shapiro ([a20], [a21]) proved the following result. Let
. Dickson's result was a starting point for much further research. In 1949 and 1968, H.N. Shapiro ([a20], [a21]) proved the following result. Let 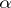 be a rational number. A necessary and sufficient condition that there exist infinitely many primitive
be a rational number. A necessary and sufficient condition that there exist infinitely many primitive 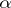 -abundant numbers (i.e.
-abundant numbers (i.e. 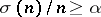 but
but  for all
for all  ,
, 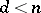 ) with
) with 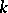 distinct prime factors is that
distinct prime factors is that  has a representation
has a representation
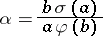 |
with 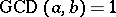 ,
, 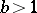 , where
, where  . Here,
. Here,  is the Euler totient function and
is the Euler totient function and 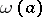 denotes the number of distinct prime factors of
denotes the number of distinct prime factors of  .
.
In 1933, F. Behrend, H. Davenport and S. Chowla [a4] showed that the density of non-deficient numbers exists and is positive. This result follows also from a theorem of P. Erdős [a7] stating that the sum of reciprocals of primitive abundant numbers converges. Let
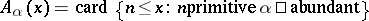 |
be the counting function of primitive  -abundant numbers. Erdős proved that [a10]
-abundant numbers. Erdős proved that [a10]
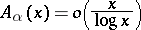 |
and that [a8]
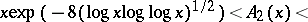 |
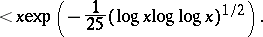 |
This was sharpened successively by A. Ivić [a13], with 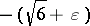 in place of
in place of 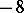 and
and  in place of
in place of 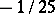 ; and by M.R. Avidon [a2], who considered
; and by M.R. Avidon [a2], who considered 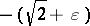 in place of
in place of 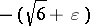 , and
, and 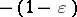 in place of
in place of 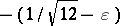 .
.
L. Alaoglu and Erdős [a1] call a number  superabundant if
superabundant if
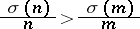 |
for all 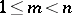 . Let
. Let 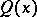 be the counting function of superabundant numbers. For two consecutive superabundant numbers
be the counting function of superabundant numbers. For two consecutive superabundant numbers  ,
, 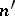 they prove that
they prove that
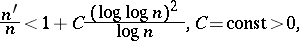 |
and this was sharpened to 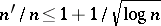 for an infinity of
for an infinity of  by J.-L. Nicolas [a16]. Alaoglu and Erdős showed that
by J.-L. Nicolas [a16]. Alaoglu and Erdős showed that 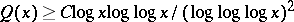 , while Erdős and Nicolas [a11] demonstrated that
, while Erdős and Nicolas [a11] demonstrated that 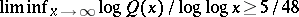 . Alaoglu and Erdős [a1] introduced also the notion of highly abundant number, a number
. Alaoglu and Erdős [a1] introduced also the notion of highly abundant number, a number  with the property that
with the property that 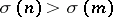 for all
for all  . For the counting function
. For the counting function 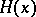 of these numbers one has
of these numbers one has 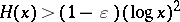 for all
for all 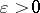 and large
and large  ; if
; if  is highly abundant, then the largest prime factor of
is highly abundant, then the largest prime factor of  is less than
is less than 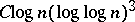 .
.
Erdős and Nicolas [a11] call a number  cube-free superabundant if
cube-free superabundant if 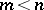 implies
implies 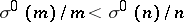 , where
, where 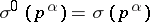 for
for 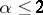 and
and 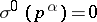 for
for 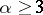 (with
(with 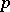 a prime number and
a prime number and 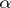 a positive integer). They prove that if
a positive integer). They prove that if 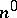 and
and 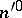 are two consecutive cube-free superabundant numbers, then
are two consecutive cube-free superabundant numbers, then 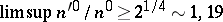 . A non-deficient number is called weird by S.J. Benkovski and Erdős [a3] if it is not pseudo-perfect (cf. also Perfect number). They proved that the density of weird numbers is positive.
. A non-deficient number is called weird by S.J. Benkovski and Erdős [a3] if it is not pseudo-perfect (cf. also Perfect number). They proved that the density of weird numbers is positive.
V. Siva Rama Prasad and D.R. Reddy [a23] say that a number  is primitive unitary
is primitive unitary 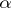 -abundant if
-abundant if 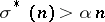 but
but 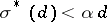 for all
for all  ,
,  (
(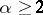 ). Here,
). Here, 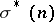 denotes the sum of unitary divisors of
denotes the sum of unitary divisors of  (for these functions, as well as related results, see also [a15]). Let
(for these functions, as well as related results, see also [a15]). Let 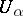 be the set of these numbers. Then
be the set of these numbers. Then
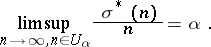 |
Miscellaneous results.
Let 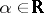 . A number
. A number  is called
is called 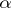 -non-deficient if
-non-deficient if 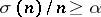 . By sharpening a result of O. Grün [a12], H. Salié [a18] proved that the least prime factor of every
. By sharpening a result of O. Grün [a12], H. Salié [a18] proved that the least prime factor of every 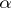 -non-deficient number with
-non-deficient number with 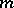 prime factors is less than
prime factors is less than 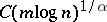 .
.
Ch.R. Wall [a24] proved that there exist infinitely many abundant integers  (with
(with  and
and  given). Let
given). Let  be fixed. Then there exist
be fixed. Then there exist  consecutive abundant numbers. There exist infinitely many sequences of five consecutive deficient numbers. (See [a25].) See [a14] for a table of odd primitive abundant numbers
consecutive abundant numbers. There exist infinitely many sequences of five consecutive deficient numbers. (See [a25].) See [a14] for a table of odd primitive abundant numbers  with five distinct prime factors for which
with five distinct prime factors for which
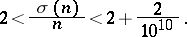 |
If 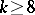 , the number
, the number 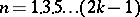 is abundant, see [a22].
is abundant, see [a22].
For others results on deficient, perfect, or related numbers, see [a15], [a8], [a9], [a19], [a17].
L. Moser [a26] proved that every integer 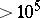 can be expressed as the sum of two abundant numbers. Actually, this is valid for integers
can be expressed as the sum of two abundant numbers. Actually, this is valid for integers 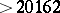 , see [a27].
, see [a27].
For a table of abundant numbers less than 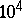 , see [a28].
, see [a28].
References
| [a1] | L. Alaoglu, P. Erdös, "On highly composite and similar numbers" Trans. Amer. Math. Soc. , 56 (1944) pp. 448–469 |
| [a2] | M.R. Avidon, "On the distribution of primitive abundant numbers" Acta Arith. , 77 (1996) pp. 195–205 |
| [a3] | S.J. Benkovski, P. Erdös, "On weird and pseudoperfect numbers" Math. Comput. , 28 (1974) pp. 617–623 |
| [a4] | H. Davenport, "Über numeri abundantes" Preuss. Akad. Wiss. Sitzungsber , 26/29 (1933) pp. 830–837 |
| [a5] | L.E. Dickson, "History of the theory of numbers" , I (Divisibility and primality) , Chelsea (1919) (Reprint: AMS 1999) |
| [a6] | L.E. Dickson, "Finiteness of odd perfect and primitive abundent numbers with  distinct prime factors" Amer. J. Math. , 35 (1913) pp. 413–422 distinct prime factors" Amer. J. Math. , 35 (1913) pp. 413–422 |
| [a7] | P. Erdös, "On the density of the abundant numbers" J. London Math. Soc. , 9 (1934) pp. 278–282 |
| [a8] | P. Erdös, "On primitive abundant numbers" J. London Math. Soc. , 9 (1935) pp. 49–58 |
| [a9] | P. Erdös, "Note on consecutive abundant numbers" J. London Math. Soc. , 13 (1938) pp. 128–131 |
| [a10] | P. Erdös, "Remarks on number theory I, On primitive 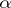 -abundant numbers" Acta Arith. , 5 (1958) pp. 25–33 -abundant numbers" Acta Arith. , 5 (1958) pp. 25–33 |
| [a11] | P. Erdös, J.-L. Nicolas, "Répartition des nombres superabondantes" Bull. Soc. Math. France , 103 (1975) pp. 65–90 |
| [a12] | O. Grün, "Über ungerade vollkommene Zahlen" Math. Z. , 55 (1952) pp. 353–354 |
| [a13] | A. Ivić, "The distribution of primitive abundant numbers" Studia Sci. Math. Hung. , 20 (1985) pp. 183–187 |
| [a14] | M. Kishore, "Odd integers  with five distinct prime factors for which with five distinct prime factors for which 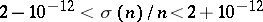 " Math. Comput. , 32 (1978) pp. 303–309 " Math. Comput. , 32 (1978) pp. 303–309 |
| [a15] | D.S. Mitrinović, J. Sándor, "Handbook of number theory" , Kluwer Acad. Publ. (1995) (In coop. with B. Crstici) |
| [a16] | J.-L. Nicolas, "Ordre maximal d'un élément du groupe 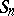 des permutations et `highly composite numbers'" Bull. Soc. Math. France , 97 (1969) pp. 129–191 des permutations et `highly composite numbers'" Bull. Soc. Math. France , 97 (1969) pp. 129–191 |
| [a17] | H.J.J. te Riele, "A theoretical and computational study of generalized aliquot sequences" Math. Centrum, Amsterdam (1975) |
| [a18] | H. Salié, "Über abundante Zahlen" Math. Nachr. , 9 (1953) pp. 217–220 |
| [a19] | J. Sándor, "On a method of Galambos and Kátai concerning the frequency of deficient numbers" Publ. Math. (Debrecen) , 39 (1991) pp. 155–157 |
| [a20] | H.N. Shapiro, "Note on a theorem of Dickson" Bull. Amer. Math. Soc. , 55 (1949) pp. 450–452 |
| [a21] | H.N. Shapiro, "On primitive abundant numbers" Commun. Pure Appl. Math. , 21 (1968) pp. 111–118 |
| [a22] | W. Sierpinski, "Teoria liczb" , II , Warsawa (1959) |
| [a23] | V. Siva Rama Prasad, D.R. Reddy, "On primitive unitary abundant numbers" Indian J. Pure Appl. Math. , 21 (1990) pp. 40–44 |
| [a24] | Ch.R. Wall, "Problem E3002" Amer. Math. Monthly , 90 (1983) pp. 400 (Solution by N.J. Fine: 93 (1986), 814) |
| [a25] | Ch.R. Wall, "Problem, 6356" Amer. Math. Monthly , 88 (1981) pp. 623 (Solution by L.L. Foster: 90 (1983), 215-216) |
| [a26] | L. Moser, "Problem E848" Amer. Math. Monthly , 56 (1949) pp. 478 |
| [a27] | E. Bach, J. Shallit, "Algorithmic number theory" , MIT (1996) pp. 334 |
| [a28] | J.W.L. Glaiser, "Number-Divisor Tables" , British Assoc. Math. Tables (1940) |
Abundant number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abundant_number&oldid=18512