Abel theorem
Abel's theorem on algebraic equations: Formulas expressing the solution of an arbitrary equation of degree  in terms of its coefficients using radicals do not exist for any
in terms of its coefficients using radicals do not exist for any 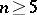 . The theorem was proved by N.H. Abel in 1824 . Abel's theorem may also be obtained as a corollary of Galois theory, from which a more general theorem follows: For any
. The theorem was proved by N.H. Abel in 1824 . Abel's theorem may also be obtained as a corollary of Galois theory, from which a more general theorem follows: For any 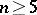 there exist algebraic equations with integer coefficients whose roots cannot be expressed in terms of radicals of rational numbers. For a modern formulation of Abel's theorem for equations over an arbitrary field, see Algebraic equation.
there exist algebraic equations with integer coefficients whose roots cannot be expressed in terms of radicals of rational numbers. For a modern formulation of Abel's theorem for equations over an arbitrary field, see Algebraic equation.
Abel's theorem on power series: If the power series
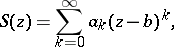 | (*) |
where 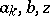 are complex numbers, converges at
are complex numbers, converges at 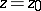 , then it converges absolutely and uniformly within any disc
, then it converges absolutely and uniformly within any disc 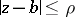 of radius
of radius 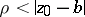 and with centre at
and with centre at 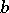 . The theorem was established by N.H. Abel . It follows from the theorem that there exists a number
. The theorem was established by N.H. Abel . It follows from the theorem that there exists a number 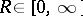 such that if
such that if 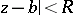 the series is convergent, while if
the series is convergent, while if 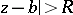 the series is divergent. The number
the series is divergent. The number  is called the radius of convergence of the series (*), while the disc
is called the radius of convergence of the series (*), while the disc 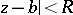 is known as the disc of convergence of the series (*).
is known as the disc of convergence of the series (*).
Abel's continuity theorem: If the power series
converges at a point 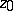 on the boundary of the disc of convergence, then it is a continuous function in any closed triangle
on the boundary of the disc of convergence, then it is a continuous function in any closed triangle 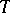 with vertices
with vertices 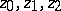 , where
, where 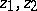 are located inside the disc of convergence. In particular
are located inside the disc of convergence. In particular
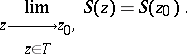 |
This limit always exists along the radius: The series
converges uniformly along any radius of the disc of convergence joining the points 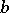 and
and 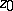 . This theorem is used, in particular, to calculate the sum of a power series which converges at the boundary points of the disc of convergence.
. This theorem is used, in particular, to calculate the sum of a power series which converges at the boundary points of the disc of convergence.
Abel's theorem on Dirichlet series: If the Dirichlet series
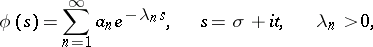 |
converges at the point 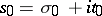 , then it converges in the half-plane
, then it converges in the half-plane 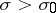 and converges uniformly inside any angle
and converges uniformly inside any angle 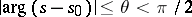 . It is a generalization of Abel's theorem on power series (take
. It is a generalization of Abel's theorem on power series (take 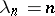 and put
and put 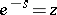 ). It follows from the theorem that the domain of convergence of a Dirichlet series is some half-plane
). It follows from the theorem that the domain of convergence of a Dirichlet series is some half-plane 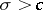 , where
, where  is the abscissa of convergence of the series.
is the abscissa of convergence of the series.
The following theorem is valid for an ordinary Dirichlet series (when 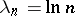 ) with a known asymptotic behaviour for the sum-function
) with a known asymptotic behaviour for the sum-function 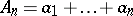 of the coefficients of the series: If
of the coefficients of the series: If
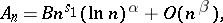 |
where 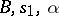 are complex numbers,
are complex numbers, 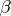 is a real number,
is a real number, 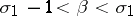 ,
, 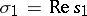 , then the Dirichlet series converges for
, then the Dirichlet series converges for 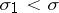 , and the function
, and the function 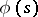 can be regularly extended to the half-plane
can be regularly extended to the half-plane 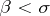 with the exception of the point
with the exception of the point 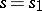 . Moreover
. Moreover
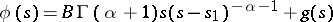 |
if 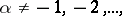 and
and
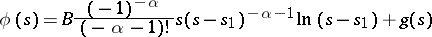 |
if 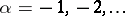 . Here
. Here 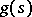 is a regular function for
is a regular function for 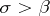 .
.
E.g., the Riemann zeta-function 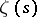 (
(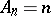 ,
, 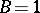 ,
,  ,
, 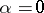 ,
, 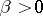 ) is regular at least in the half-plane
) is regular at least in the half-plane 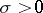 , with the exception of the point
, with the exception of the point 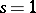 at which it has a first-order pole with residue
at which it has a first-order pole with residue 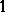 . This theorem can be generalized in various ways. E.g., if
. This theorem can be generalized in various ways. E.g., if
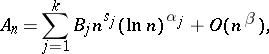 |
where 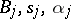 (
(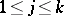 ), are arbitrary complex numbers, and
), are arbitrary complex numbers, and 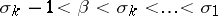 , then the Dirichlet series converges for
, then the Dirichlet series converges for 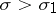 , and
, and 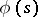 is regular in the domain
is regular in the domain 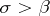 with the exception of the points
with the exception of the points  at which it has algebraic or logarithmic singularities. Theorems of this type yield information on the behaviour of the Dirichlet series in a given half-plane, based on the asymptotic behaviour of
at which it has algebraic or logarithmic singularities. Theorems of this type yield information on the behaviour of the Dirichlet series in a given half-plane, based on the asymptotic behaviour of 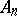 .
.
References
| [1] | N.H. Abel, , Oeuvres complètes, nouvelle éd. , 1 , Grondahl & Son , Christiania (1881) (Edition de Holmboe) |
| [2] | N.H. Abel, "Untersuchungen über die Reihe 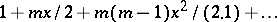 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
Comments
More on Abel's theorems 2)–4) can be found in [a1].
References
| [a1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
Abel theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_theorem&oldid=14629