AM-compact operator
One of the most interesting classes of linear operators between Banach spaces is that of compact operators (cf. also Banach space; Linear operator; Compact operator). When the Banach spaces have some order structure (concretely: if they are Banach lattices; cf. also Banach lattice; Vector lattice; Banach function space), there are some natural classes of operators, containing the compact operators, which also have good properties and better behaviour respect to the order structure. One of these classes is that of the so-called AM-compact operators, introduced by P.S. Dodds and D.H. Fremlin in [a2] and defined as follows. Let  ,
,  be Banach lattices. A linear operator
be Banach lattices. A linear operator  is called AM-compact if
is called AM-compact if  maps order-bounded sets onto relatively compact sets.
maps order-bounded sets onto relatively compact sets.
Clearly, every compact operator is AM-compact. The converse is true if  has a strong unit (i.e., there exists an
has a strong unit (i.e., there exists an  ,
, 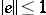 , such that
, such that  implies
implies  ). If
). If 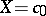 or
or 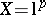 , where
, where 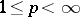 , then every continuous linear operator
, then every continuous linear operator 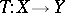 is AM-compact, but needs not be compact. There are important classes of operators related with the AM-compact operators. Among them are the absolute integral operators and the Dunford–Pettis operators. In particular, one has that if
is AM-compact, but needs not be compact. There are important classes of operators related with the AM-compact operators. Among them are the absolute integral operators and the Dunford–Pettis operators. In particular, one has that if  and
and  are Banach function spaces, with
are Banach function spaces, with 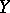 having order-continuous norm (cf. also Banach function space), then every absolute integral operator from
having order-continuous norm (cf. also Banach function space), then every absolute integral operator from  into
into  is AM-compact (see [a6]). It is known (see, for instance [a3]) that if
is AM-compact (see [a6]). It is known (see, for instance [a3]) that if  is a Dunford–Pettis operator and
is a Dunford–Pettis operator and 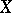 has order-continuous norm, then
has order-continuous norm, then 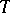 is AM-compact, while if
is AM-compact, while if 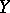 is also an
is also an  -space (for instance, if
-space (for instance, if 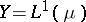 ), then the converse is also true.
), then the converse is also true.
AM-compact operators, in contrast to compact operators, have a good behaviour respect to the order in the space 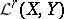 of all regular operators between the Banach lattices
of all regular operators between the Banach lattices  and
and  . If
. If 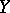 has order-continuous norm, the collection of all regular AM-compact operators forms a band (cf. also Riesz space; Semi-ordered space) in
has order-continuous norm, the collection of all regular AM-compact operators forms a band (cf. also Riesz space; Semi-ordered space) in  ; consequently, if
; consequently, if 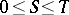 and
and 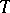 is AM-compact, then
is AM-compact, then 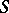 is also AM-compact.
is also AM-compact.
Positive operators in Banach lattices have interesting spectral properties (see, for instance, [a5] and [a3]): the spectral radius is monotone (i.e., if 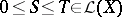 , then
, then 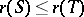 ), and the spectral radius of a positive operator is in the spectrum. In general, these two properties fail for the essential spectrum,
), and the spectral radius of a positive operator is in the spectrum. In general, these two properties fail for the essential spectrum, 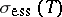 , and the essential spectral radius,
, and the essential spectral radius, 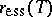 (cf. also Spectrum of an operator). However, B. de Pagter and A.R. Schep [a4] have established that these properties are true for AM-compact operators; they prove that if
(cf. also Spectrum of an operator). However, B. de Pagter and A.R. Schep [a4] have established that these properties are true for AM-compact operators; they prove that if 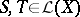 are positive operators with
are positive operators with 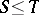 and
and  AM-compact, then
AM-compact, then 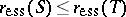 and
and 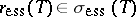 . In [a1] a representation space for the essential spectrum of AM-compact operators is constructed; using this representation space the results mentioned above can be obtained with a different technique, as well as some results concerning the cyclicity of the essential spectrum for AM-compact operators.
. In [a1] a representation space for the essential spectrum of AM-compact operators is constructed; using this representation space the results mentioned above can be obtained with a different technique, as well as some results concerning the cyclicity of the essential spectrum for AM-compact operators.
References
| [a1] | F. Andreu, V. Caselles, J. Martinez, J.M. Mazon, "The essential spectrum of AM-compact operators" Indag. Math. N.S. , 2 (1991) pp. 149–158 |
| [a2] | P.S. Dodds, D.H. Fremlin, "Compact operators in Banach lattices" Israel J. Math. , 34 (1979) pp. 287–320 |
| [a3] | P. Meyer-Nieberg, "Banach lattices" , Springer (1991) |
| [a4] | B. de Pagter, A.R. Schep, "Measures of non-compactness of operators on Banach lattices" J. Funct. Anal. , 78 (1988) pp. 31–55 |
| [a5] | H.H. Schaefer, "Banach lattices and positive operators" , Springer (1974) |
| [a6] | A.C. Zaanen, "Riesz spaces" , II , North-Holland (1983) |
AM-compact operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=AM-compact_operator&oldid=15166