Iwasawa theory
A theory of $\mathbf{Z} _ { p }$-extensions introduced by K. Iwasawa [a8]. Its motivation has been a strong analogy between number fields and curves over finite fields. One of the most fruitful results in this theory is the Iwasawa main conjecture, which has been proved for totally real number fields [a19]. The conjecture is considered as an analogue of Weil's result that the characteristic polynomial of the Frobenius automorphism acting on the Jacobian of a curve over a finite field is the essential part of the zeta-function of the curve. A lot of methods and ideas developed in the theory appeared to be widely applicable and have given rise to major advances, for example, results on the Birch–Swinnerton-Dyer conjecture [a3], [a6], [a16], [a22] and on Fermat's last theorem [a20] (cf. also Fermat last theorem). For details and generalizations of Iwasawa theory, see [a10], [a7], [a12], [a18].
$\mathbf{Z} _ { p }$-extension of a number field.
Let $p$ be a prime number and let $k$ be a finite extension of the rational number field $\mathbf{Q}$. A $\mathbf{Z} _ { p }$-extension of $k$ is an extension $K / k$ with $\operatorname{Gal}( K / k ) \cong \mathbf{Z} _ { p }$, where $\mathbf{Z} _ { p }$ is the additive group of $p$-adic integers. Then there is a sequence of fields
\begin{equation*} k = k _ { 0 } \subset k _ { 1 } \subset \ldots \subset k _ { n } \subset \ldots \subset K = \bigcup _ { n \geq 0 } k _ { n }, \end{equation*}
where $k _ { n }$ is a cyclic extension of $k$ of degree $p ^ { n }$. Class field theory shows that there are at least $1 + r _ { 2 } ( k )$ independent $\mathbf{Z} _ { p }$-extensions of $k$ (cf. below, the section Leopoldt conjecture). Every $k$ has at least one $\mathbf{Z} _ { p }$-extension, namely the cyclotomic $\mathbf{Z} _ { p }$-extension $k _ { \infty }$. It is obtained by letting $k _ { \infty }$ be an appropriate subfield of $\cup _ { n \geq 0 } k ( \mu _ { p ^ n} )$, where $\mu _ { \mathcal{m} }$ is the group of $m$th roots of unity.
Leopoldt conjecture.
Let $E _ { 1 } ( k )$ be the group of units of $k$ which are congruent to $1$ modulo every prime ideal $\mathfrak{p}$ of $k$ lying above $p$. By Dirichlet's unit theorem, $\operatorname{rank}_{\mathbf{Z}} E _ { 1 } ( k ) = r _ { 1 } ( k ) + r _ { 2 } ( k ) - 1$, where $r _ { 1 } ( k )$ (resp. $2 r_ 2 ( k )$) is the number of embeddings of $k$ in $\mathbf{R}$ (resp. $\mathbf{C}$). Let $U _ { 1 , \mathfrak p }$ be the group of local units of $k _ { \mathfrak p }$ congruent to $1$ modulo $\mathfrak{p}$. There is an embedding $E _ { 1 } ( k ) \rightarrow \prod _ { \mathfrak{p} | p } U _ { 1 , \mathfrak{p} }$ ($\varepsilon \mapsto ( \varepsilon , \ldots , \varepsilon )$). Let $\overline{E} _ { 1 } ( k )$ denote the topological closure of the image. It is Leopoldt's conjecture that the equality
\begin{equation*} \operatorname{ rank }_Z E _ { 1 } ( k ) = \operatorname { rank } _ { Z p } \overline{E} _ { 1 } ( k ) \end{equation*}
holds for every $k$. A. Brumer [a1] proved the conjecture for Abelian extensions $k / \mathbf{Q}$ (or an imaginary quadratic field). Put $\delta _ { p } ( k ) = \operatorname { rank } _ {\bf Z } \overline{E} _ { 1 } ( k ) - \operatorname { rank } _ { {\bf Z} _ { p } } E _ { 1 } ( k ) \geq 0$. Then class field theory shows that there are $1 + r _ { 2 } ( k ) + \delta _ { p } ( k )$ independent $\mathbf{Z} _ { p }$-extensions of $k$.
Iwasawa module.
Let $\mathcal{O}$ be the integer ring of a finite extension of $\mathbf{Q} _ { p }$ and $\pi$ a uniformizer of $\mathcal{O}$. Let $\Gamma$ be a compact Abelian group isomorphic to $\mathbf{Z} _ { p }$ and $R = {\cal O} [ [ \Gamma ] ] = \text { varprojlim } {\cal O} [ \Gamma / \Gamma ^ { p ^ { n } } ]$, where the inverse limit is taken with respect to $\Gamma / \Gamma ^ { p^m } \rightarrow \Gamma / \Gamma ^ { p ^n }$ ($\gamma \operatorname{mod} \Gamma ^ { p^m } \mapsto \gamma \operatorname { mod } \Gamma ^ { p ^ { n } }$) for $m \geq n$. Fix a topological generator $\gamma$ of $\Gamma$. Let $\Lambda = \mathcal{O} [ [ T ] ]$ be the ring of formal power series in an indeterminate $T$ with coefficients in $\mathcal{O}$. $P ( T ) \in \mathcal{O} [ T ]$ is called a distinguished polynomial if $P ( T ) = T ^ { n } + a _ { n - 1 } T ^ { n - 1 } + \ldots + a _ { 0 }$ with $a _ { i } \in ( \pi )$ for $0 \leq i \leq n - 1$. The prime ideals of $\Lambda$ are $0$, $( \pi , T )$, $( \pi )$, $( P ( T ) )$, where $P ( T )$ is distinguished and irreducible. The classification of compact $R$-modules in [a8] was simplified by J.-P. Serre, who pointed out that $R$ is topologically isomorphic to $\Lambda$, hence each compact $R$-module $X$ admits the unique structure of a compact $\Lambda$-module such that $( 1 + T ) x = \gamma . x$ for every $x \in X$. Finitely-generated $\Lambda$-modules are called Iwasawa modules. They are classified as follows: for an Iwasawa module $X$, there is a $\Lambda$-homomorphism
\begin{equation*} \varphi : X \rightarrow \Lambda ^ { r } \bigoplus\bigoplus _ { i = 1 } ^ { s } \Lambda / (\, f _ { i } ( T ) ^ { l _i} ) \bigoplus \bigoplus _ { j = 1 } ^ { t } \Lambda / ( \pi ^ { m _ { j } } ) \end{equation*}
with $\operatorname{Ker} \varphi$ and $\operatorname {Coker} \varphi$ finite $\Lambda$-modules, where $r , s , l _ { i } , t , m_ { j } \in \mathbf{Z}_{ \geq 0}$ and $f _ { i } ( T )$ is distinguished and irreducible. For a torsion $\Lambda$-module $X$, i.e., $r = 0$, one defines
\begin{equation*} \operatorname { char } ( X ) = \prod _ { i = 1 } ^ { s } f _ { i } ( T ) ^ { l _ { i } } \prod _ { j = 1 } ^ { t } \pi ^ { m _ { j } }, \end{equation*}
\begin{equation*} \lambda ( X ) = \sum _ { i = 1 } ^ { s } \operatorname { deg } ( f _ { i } ( T ) ^ { l _ { i } } ) , \ \mu ( X ) = \sum _ { j = 1 } ^ { t } m _ { j }. \end{equation*}
Iwasawa invariant.
Let $K / k$ be a $\mathbf{Z} _ { p }$-extension. Let $A _ { n } ( k )$ denote the $p$-Sylow subgroup of the ideal class group of $k _ { n }$. Let $p ^ { e_n}$ be the order of $A _ { n } ( k )$. Iwasawa [a8] proved that there exist integers $\lambda _ { p } ( K / k ) \geq 0$, $\mu _ { p } ( K / k ) \geq 0$ and $\nu _ { p } ( K / k )$ such that
\begin{equation*} e _ { n } = \lambda _ { p } ( K / k ) n + \mu _ { p } ( K / k ) p ^ { n } + \nu _ { p } ( K / k ) \end{equation*}
for all sufficiently large $n$. The invariants $\lambda _ { p } ( K / k )$ and $\mu _ { p } ( K / k )$ can be obtained from the Iwasawa module $X = \text { varprojlim } A _ { n } ( k )$, where the inverse limit is taken with respect to the relative norm mappings. Put $\Gamma = \operatorname { Gal } ( K / k )$. $X$ is a compact $R = \mathbf{Z} _ { p } [ [ \Gamma ] ]$-module in a natural way. One fixes a topological generator $\gamma$ of $\Gamma$. Then $X$ is considered as a compact $\Lambda = {\bf Z} _ { p } [ [ T ] ]$-module (cf. the section on Iwasawa module above). Since $A _ { n } ( k )$ is finite, $X$ is a finitely-generated torsion $\Lambda$-module. One has that $\lambda _ { p } ( K / k ) = \lambda ( X )$ and $\mu _ { p } ( K / k ) = \mu ( X )$.
Iwasawa [a9] constructed infinitely many non-cyclotomic $\mathbf{Z} _ { p }$-extensions $K / k$ with $\mu _ { p } ( K / k ) > 0$. There are infinitely many $\mathbf{Z} _ { p }$-extensions $K / k$ with $\lambda _ { p } ( K / k ) > 0$. For $k = \mathbf{Q} ( \mu _ { p } )$, $\lambda _ { p } ( k _ { \infty } / k ) > 0$ if and only if $p$ is irregular (cf. also Irregular prime number). It is Iwasawa's conjecture that $\mu _ { p } ( k _ { \infty } / k ) = 0$ for every $k$. B. Ferrero and L. Washington [a5] proved this conjecture for Abelian extensions $k / \mathbf{Q}$. W. Sinnott [a17] gave a new proof of this using the $\Gamma$-transform of a rational function.
It is Greenberg's conjecture that $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = 0$ for every totally real $k$. For small $p$, it was proved that there are infinitely many real quadratic fields $k$ with $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = \nu _ { p } ( k _ { \infty } / k ) = 0$ [a14], [a15]. There exists a lot of numerical work verifying this conjecture, mainly for real quadratic fields.
It is Vandiver's conjecture that $p$ does not divide the class number of the maximal real subfield $k$ of ${\bf Q} ( \mu _ { p } )$ for all $p$, which implies that $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = \nu _ { p } ( k _ { \infty } / k ) = 0$. This conjecture was verified for all $p < 12000000$ [a2].
Iwasawa main conjecture.
Let $p$ be an odd prime number and $k$ a totally real number field. Fix an embedding of $\overline{\mathbf{Q}}$ into $\overline {\bf Q } _ { p }$. Let 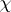 be a $p$-adic valued Artin character for $k$ of order prime to $p$. Let $ { k }_\chi$ be the extension of $k$ attached to
be a $p$-adic valued Artin character for $k$ of order prime to $p$. Let $ { k }_\chi$ be the extension of $k$ attached to 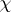 . Assume that $ { k }_\chi$ is also totally real. Fix a topological generator $\gamma$ of $\Gamma = \operatorname { Gal } ( k _ { \chi , \infty } / k _ { \chi } ) \cong \operatorname { Gal } ( k _ { \chi } ( \mu _ { p } \infty ) / k _ { \chi } ( \mu _ { p } ) )$ and let $u \in \mathbf{Z} _ { p } ^ { \times }$ be such that $\zeta ^ { \gamma } = \zeta ^ { u }$ for all $\zeta \in \mu _ { p ^ \infty}$.
. Assume that $ { k }_\chi$ is also totally real. Fix a topological generator $\gamma$ of $\Gamma = \operatorname { Gal } ( k _ { \chi , \infty } / k _ { \chi } ) \cong \operatorname { Gal } ( k _ { \chi } ( \mu _ { p } \infty ) / k _ { \chi } ( \mu _ { p } ) )$ and let $u \in \mathbf{Z} _ { p } ^ { \times }$ be such that $\zeta ^ { \gamma } = \zeta ^ { u }$ for all $\zeta \in \mu _ { p ^ \infty}$.
Let $\omega$ be the Teichmüller character
\begin{equation*} \omega : \operatorname { Gal } ( k ( \mu _ { p } ) / k ) \rightarrow {\bf Z} _ { p } ^ { \times } ( \omega ( a ) \equiv a \operatorname { mod } p ) \end{equation*}
and let $L ( s , \chi )$ be the classical $L$-function for $k$. Following T. Kubota and H.W. Leopoldt [a11], P. Deligne and K. Ribet [a4] proved the existence of a $p$-adic $L$-function $L _ { p } ( s , \chi )$ on $s \in \mathbf{Z} _ { p }$ ($s \neq 1$ if 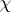 is trivial) satisfying the following interpolation property:
is trivial) satisfying the following interpolation property:
\begin{equation*} L _ { p } ( 1 - n , \chi ) = L ( 1 - n , \chi \omega ^ { - n } ) \prod _ { {\frak p} | p } ( 1 - \chi \omega ^ { - n } ( {\frak p} ) N {\frak p} ^ { n - 1 } ) \end{equation*}
for $n \geq 1$. There exists a unique power series $G _ { \chi } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ such that $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 )$ (if 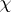 is trivial, $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 ) / ( u ^ { s } - 1 )$), where $\mathbf{Z} _ { p } [ \chi ]$ is the ring generated over $\mathbf{Z} _ { p }$ by the values of
is trivial, $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 ) / ( u ^ { s } - 1 )$), where $\mathbf{Z} _ { p } [ \chi ]$ is the ring generated over $\mathbf{Z} _ { p }$ by the values of 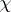 . By the $p$-adic Weierstrass preparation theorem (cf. also Weierstrass theorem), one can write $G _ { \chi } ( T ) = \pi ^ { \mu_\chi } g _ { \chi } ( T ) u _ { \chi } ( T )$, where $\mu _ { \chi } \in \mathbf{Z} _ { \geq 0 }$, $g _ { \chi } ( T )$ is a distinguished polynomial, $\pi$ is a uniformizer of $\mathbf{Z} _ { p } [ \chi ]$, and $u _ { \chi } ( T )$ is a unit power series. Let $G _ { \chi } ^ { * } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ be such that $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 )$ (if
. By the $p$-adic Weierstrass preparation theorem (cf. also Weierstrass theorem), one can write $G _ { \chi } ( T ) = \pi ^ { \mu_\chi } g _ { \chi } ( T ) u _ { \chi } ( T )$, where $\mu _ { \chi } \in \mathbf{Z} _ { \geq 0 }$, $g _ { \chi } ( T )$ is a distinguished polynomial, $\pi$ is a uniformizer of $\mathbf{Z} _ { p } [ \chi ]$, and $u _ { \chi } ( T )$ is a unit power series. Let $G _ { \chi } ^ { * } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ be such that $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 )$ (if 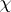 is trivial, $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 ) / ( u ^ { s } - u )$). One can similarly define $\mu _ { \chi } ^ { * } = \mu _ { \chi }$ and a distinguished polynomial $g _ { \chi } ^ { * } ( T )$ for $G _ { \chi } ^ { * } ( T )$.
is trivial, $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 ) / ( u ^ { s } - u )$). One can similarly define $\mu _ { \chi } ^ { * } = \mu _ { \chi }$ and a distinguished polynomial $g _ { \chi } ^ { * } ( T )$ for $G _ { \chi } ^ { * } ( T )$.
Let $k ^ { \prime } = k _ { \chi } ( \mu _ { p } )$, let $L ( k ^ { \prime } )$ be the maximal unramified Abelian $p$-extension of $k _ { \infty } ^ { \prime }$ and $M ( k ^ { \prime } )$ the maximal Abelian $p$-extension of $k _ { \infty } ^ { \prime }$, which are both unramified outside the primes above $p$. By class field theory, $\operatorname {Gal}( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \cong \text { varprojlim } A _ { n } ( k ^ { \prime } )$. Extend $g \in \operatorname { Gal } ( k _ { \infty } ^ { \prime } / k )$ to $\tilde{g} \in \operatorname { Gal } ( L ( k ^ { \prime } ) / k )$. Then $g$ acts on $x \in \operatorname { Gal } ( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } )$ by $g.x = \tilde{g} x \tilde{g} ^ { - 1 }$. Put $X = \operatorname { Gal } ( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \otimes \mathbf{Z} _ { p } [ \chi ]$ and $Y = \operatorname { Gal } ( M ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \otimes \mathbf{Z} _ { p } [ \chi ]$. Let $\Delta = \text { Gal } ( k _ { \infty } ^ { \prime } / k _ { \infty } ) \cong \text { Gal } ( k ^ { \prime } / k )$,
\begin{equation*} X ^ { \omega \chi ^ { - 1 }} = \{ x \in X : \delta . x = \omega \chi ^ { - 1 } ( \delta ) x \text{ for } \delta \in \Delta \}, \end{equation*}
\begin{equation*} Y ^ { \chi } = \{ y \in Y : \delta \cdot y = \chi ( \delta ) y \, \text { for } \delta \in \Delta \}. \end{equation*}
Then one can regard $X ^ { \omega } \chi ^ { - 1 }$ and $Y^{\chi}$ as $\Lambda = \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$-modules.
Following [a13], A. Wiles proved the following equality, i.e., the Iwasawa main conjecture for totally real fields:
\begin{equation*} \operatorname{char}( X ^ { \omega \chi ^ { - 1 }} ) = \pi ^ { \mu _ { \chi } ^ { * } } g _ { \chi } ^ { * } ( T ). \end{equation*}
This equality is equivalent to
\begin{equation*} \operatorname { char } ( Y ^ { \chi } ) = \pi ^ { \mu _{\chi}} g _ { \chi } ( T ). \end{equation*}
The proof uses delicate techniques from modular forms, especially Hida's theory of modular forms, to construct unramified extensions.
Following Stickelberger's theorem, F. Thaine and V. Kolyvagin invented techniques for constructing relations in ideal class groups. These methods, which use Gauss sums (cyclotomic units or elliptic units) satisfying properties known as the Euler system, have given elementary proofs of the Iwasawa main conjecture for $k = \mathbf{Q}$ [a12], [a21].
References
| [a1] | A. Brumer, "On the units of algebraic number fields" Mathematika , 14 (1967) pp. 121–124 MR0220694 Zbl 0171.01105 |
| [a2] | J. Buhler, R. Crandall, R. Ernvall, T. Metsänkylä, M.A. Shokrollahi, "Irregular primes and cyclotomic invariants to 12 million" J. Symbolic Comput. , 31 (2001) pp. 89–96 MR1806208 Zbl 1001.11061 |
| [a3] | J. Coates, A. Wiles, "On the conjecture of Birch and Swinnerton-Dyer" Invent. Math. , 39 (1977) pp. 223–251 MR0463176 Zbl 0359.14009 |
| [a4] | P. Deligne, K. Ribet, "Values of abelian $L$-functions at negative integers over totally real fields" Invent. Math. , 59 (1980) pp. 227–286 MR579702 |
| [a5] | B. Ferrero, L. Washington, "The Iwasawa invariant $\mu _ { p }$ vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001 |
| [a6] | R. Greenberg, "On the Birch and Swinnerton-Dyer conjecture" Invent. Math. , 72 (1983) pp. 241–265 MR0700770 Zbl 0546.14015 |
| [a7] | K. Iwasawa, "On $\mathbf{Z}_l$-extensions of algebraic number fields" Ann. of Math. , 98 (1973) pp. 246–326 MR349627 |
| [a8] | K. Iwasawa, "On $\Gamma$-extensions of algebraic number fields" Bull. Amer. Math. Soc. , 65 (1959) pp. 183–226 MR124316 |
| [a9] | K. Iwasawa, "On the $\mu$-invariants of $\mathbf{Z}_l$-extensions" , Number Theory, Algebraic Geometry and Commutative Algebra, in honor of Y. Akizuki , Kinokuniya (1973) pp. 1–11 MR357371 |
| [a10] | J. Coates, R. Greenberg, B. Mazur, I. Satake, "Algebraic Number Theory—In Honor of K. Iwasawa" , Adv. Studies in Pure Math. , 17 , Acad. Press (1989) Zbl 0721.00006 |
| [a11] | T. Kubota, H.W. Leopoldt, "Eine $p$-adische Theorie der Zetawerte, I. Einführung der $p$-adischen Dirichletschen $L$-Funktionen" J. Reine Angew. Math. , 214/215 (1964) pp. 328–339 MR0163900 |
| [a12] | S. Lang, "Cyclotomic fields I—II" , Graduate Texts in Math. , 121 , Springer (1990) (with an appendix by K. Rubin) |
| [a13] | B. Mazur, A. Wiles, "Class fields of abelian extensions of $\mathbf{Q}$" Invent. Math. , 76 (1984) pp. 179–330 MR0742853 Zbl 0545.12005 |
| [a14] | J. Nakagawa, K. Horie, "Elliptic curves with no rational points" Proc. Amer. Math. Soc. , 104 (1988) pp. 20–24 MR0958035 Zbl 0663.14023 |
| [a15] | K. Ono, "Indivisibility of class numbers of real quadratic fields" Compositio Math. , 119 (1999) pp. 1–11 MR1711515 Zbl 1002.11080 |
| [a16] | K. Rubin, "Tate–Shafarevich groups and $L$-functions of elliptic curves with complex multiplication" Invent. Math. , 89 (1987) pp. 527–560 MR0903383 |
| [a17] | W. Sinnott, "On the $\mu$-invariant of the $\Gamma$-transform of a rational function" Invent. Math. , 75 (1984) pp. 273–282 MR732547 |
| [a18] | L. Washington, "Introduction to cyclotomic fields" , Graduate Texts in Math. , 83 , Springer (1997) (Edition: Second) MR1421575 Zbl 0966.11047 |
| [a19] | A. Wiles, "The Iwasawa conjecture for totally real fields" Ann. of Math. , 131 (1990) pp. 493–540 MR1053488 Zbl 0719.11071 |
| [a20] | A. Wiles, "Modular elliptic curves and Fermat's last theorem" Ann. of Math. , 141 (1995) pp. 443–551 |
| [a21] | K. Rubin, "The "main conjectures" of Iwasawa theory for imaginary quadratic fields" Invent. Math. , 103 (1991) pp. 25–68 MR1157660 MR1143122 MR1136002 MR1124840 MR1110401 MR1079839 MR1034427 Zbl 0946.60500 Zbl 0825.62832 Zbl 0773.55002 Zbl 0743.76074 Zbl 0741.11028 Zbl 0737.11030 |
| [a22] | K. Rubin, "Euler systems and modular elliptic curves" , Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996) , London Math. Soc. Lecture Notes , 284 , Cambridge Univ. Press (1998) pp. 351–367 MR1696493 Zbl 0952.11016 |
Iwasawa theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Iwasawa_theory&oldid=50331