Quantum computation, theory of
The study of the model of computation in which the state space consists of linear superpositions of classical configurations and the computational steps consist of applying local unitary operators and measurements as permitted by quantum mechanics.
Quantum computation emerged in the 1980s when P. Benioff and R. Feynman realized that the apparent exponential complexity in simulating quantum physics could be overcome by using a sufficiently well controlled quantum mechanical system to perform a simulation. Quantum Turing machines were introduced by D. Deutsch in 1985 (cf. also Turing machine). Initial work focused on how quantum mechanics (cf. also Quantum field theory) could be used to implement classical computation (computation in the sense of A. Church and A.M. Turing), and on analyzing whether the quantum Turing machine model provided a universal model of computation. In the early 1990s, Deutsch and R. Jozsa found an oracle problem that could be solved faster on an error-free quantum computer than on any deterministic classical computer. E. Bernstein and U. Vazirani then formalized the notion of quantum complexity from a theoretical computer science point of view, and showed that with respect to oracles that reversibly compute classical functions, quantum computers are super-polynomially more efficient than classical computers. The gap was soon improved to an exponential one. This work culminated in the discovery, by P. Shor, of an efficient (that is, consuming only polynomial resources) algorithm for factoring large numbers and for computing discrete logarithms. It implied that widely-used public-key cryptographic systems would be insecure if quantum computers were available. Subsequently, L. Grover found an algorithm which permitted a square-root speed-up of unstructured search. Finding new algorithmic improvements achievable with quantum computers which are not reducible to Shor's or Grover's algorithm is currently (2000) an active research area. Also of great current interest is understanding how the problem of simulating quantum systems, known to be tractable on a quantum computer, relates to the problems conventionally studied within classical computational complexity theory (cf. also Complexity theory; Computational complexity classes). Comprehensive introductions to quantum computation and the known quantum algorithms may be found in [a2], [a1].
The algorithmic work described above firmly established the field of quantum computation in computer science. However, it was initially unclear whether quantum computation was a physically realizable model. Particularly worrisome was the fact that, in nature, quantum effects are rarely observable because physical noise processes tend to rapidly remove the necessary phase relationships. To solve the problem of quantum noise, Shor and A. Steane introduced quantum error-correcting codes (cf. also Error-correcting code). This idea was expanded and applied by several research groups to prove that under physically reasonable assumptions, fault tolerant quantum computation is possible. Among the assumptions are the requirements that quantum noise is sufficiently weak (below some constant threshold error per quantum bit and operation), and that the basic operations can be performed in parallel. As a result, there are now many intense experimental efforts devoted toward realizing quantum computation in a wide and increasing variety of physical systems. Progress to date (2000) has been modest, with existing systems limited to just a few qubits (quantum bits), and on the order of one hundred operations [a5].
Models of quantum computation largely parallel and generalize the classical models of computation. In particular, for formal studies of complexity, many researchers use various versions of quantum Turing machines (cf. also Turing machine), while quantum random access machines or quantum networks (also known as quantum circuits) are preferred for describing and investigating specific algorithms. To obtain a quantum version of a classical model of deterministic computation, one begins with the classical model's state space. The classical state space usually consists of an enumerable set of configurations $\psi _ { i }$, with index $i$ often constructed from strings of symbols. The quantum model associates to each $\psi _ { i }$ a member of a standard orthonormal basis $| i \rangle$ (called classical or logical states) of a Hilbert space $\mathcal{H}$. The states of the quantum model are given by "superpositions" of these basis states, which are unit vectors in $\mathcal{H}$. The classical model's initial state $\psi_0$ becomes the quantum model's initial state $| 0 \rangle$, and the classical model's transition function is replaced by a unitary operator $U$ acting on $\mathcal{H}$. $U$ has to satisfy certain locality restrictions that imply, for example, that $U | i \rangle$ must be a superposition of classical states that are accessible by an allowed classical transition function in one step from $\psi _ { i }$. The computation's answer can be obtained by measuring the state after each step. In the simplest case, the classical computation's answer is determined by whether the configuration is an "accepting" one. Accepting configurations form a set $\mathcal{A}$ which may be associated with the closed subspace of $\mathcal{H}$ spanned by the corresponding classical states. Let $P$ be the projection operator onto this subspace. If the state of the quantum model is $| {\phi} \rangle$, measurement has two possible outcomes. Either the new state is $P | \phi \rangle / \| P | \phi \rangle \|$ with probability $p = \| P | \phi \rangle \| ^ { 2 }$, in which case the computation "accepts" , or the state is $\left. ( 1 - P ) | \phi \rangle \middle/ \| ( 1 - P ) | \phi \rangle \|\right.$ with probability $1 - p$, in which case the computation continues. The possible measurement outcomes can be expanded by adding a set of "rejecting" states. In the early days of quantum computation there were lively discussions of how quantum Turing machines should halt, implying different rules about when measurements are applied during a computation.
The method outlined above for obtaining a quantum model of computation from a classical model yields a generalization of the classical model restricted to reversible transition functions. This implies that quantum complexity classes do not necessarily enlarge the classical analogues, particularly for the low-lying classes or when restricted models of computation (for example, finite state automata) are involved. To obtain a generalization of the usual model of computation it suffices to extend the set of transition operators with suitable irreversible ones. One way to do that is to allow transition operators which are the composition of a measurement (satisfying an appropriate locality constraint) followed by unitary operators depending on the measurement outcome. A different approach which works well for random access machines (RAMs) is to enhance the RAM by giving it access to an unbounded number of quantum bits which can be controlled by applying quantum gates (cf. Quantum information processing, science of). This is in effect how existing quantum algorithms are described and analyzed.
As in classical complexity studies, resources considered for quantum complexity include time and space (cf. also Complexity theory). In the context of irreversible processes, an additional resource that may be considered is entropy generated by irreversible operations. When analyzing algorithms based on quantum RAMs, it is also useful to separately account for classical and quantum resources. It is important to realize that if the complex coefficients of the unitary transition operators are rational (or, in general, computable complex numbers), then there is no difference between classical and quantum computability. Thus, the functions computable by quantum Turing machines are the same as those computable by classical Turing machines.
An important issue in studying quantum models of computation is how to define the computation's "answer" given that the output is intrinsically probabilistic. How this is defined can affect complexity classes. Guidance comes from studies of probabilistic (or randomized) computation, where the same issues arise. Since quantum computation with irreversibility can be viewed as a generalization of probabilistic computation, most comparisons of the quantum and classical complexity of algorithmic problems use bounds on the efficiency of probabilistic algorithms.
The best known quantum complexity class is the class of bounded-error quantum polynomial-time computable languages ($\mathbf{BQP}$). This is the class of languages decided in polynomial time with probability $> 2 / 3$ (acceptance) and $< 1 / 3$ (rejection) by a quantum Turing machine. Based on the oracle computing studies, the quantum factoring algorithm, and the difficulty of classically simulating quantum physics, it is conjectured that $\mathbf{BQP}$ strictly contains $\mathbf{BPP}$ (the class of bounded-error polynomial-time computable languages for the model of probabilistic classical computation). $\mathbf{BQP}$ is contained in $\mathcal{P} ^ { \# _\mathcal{ P}}$ (the class of languages decidable in polynomial time on a classical Turing machine given access to an oracle for computing the permanent of $0$-$1$ matrices — this class is contained in the class 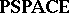 of languages computable using polynomial working space). Thus, a proof of the important conjecture that $\mathbf{BQP}$ is strictly larger than $\mathbf{BPP}$ will imply the long-sought result in classical computational complexity that
of languages computable using polynomial working space). Thus, a proof of the important conjecture that $\mathbf{BQP}$ is strictly larger than $\mathbf{BPP}$ will imply the long-sought result in classical computational complexity that 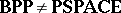 .
.
The relationship of $\mathbf{BQP}$ to $\cal N P$ (the class of non-deterministic polynomial-time languages) is not known, though it is conjectured that $\mathcal{NP} \not< \mathbf{BQP}$. If this is not the case, it would have immense practical significance, as many combinatorial optimization problems are in $\cal N P$ (cf. also $\cal N P$). One reason for thinking that $\mathcal{NP} \not< \mathbf{BQP}$ is the fact that Grover's algorithm provides the optimal speedup for unstructured quantum search, and it is widely believed that the reason for the difficulty of solving $\cal N P$-complete problems is that it is essentially equivalent to searching an unstructured search space. A generalization of unstructured search involves determining properties of (quantum) oracles by means of queries. In classical computation, an oracle is a function $f$ with values in $\{ 0,1 \}$. The corresponding quantum oracle applies the unitary operator $\hat { f }$ defined on basis states by $\widehat { f } | x , 0 , w \rangle \rightarrow | x , f ( x ) , w \rangle$ and $\hat { f } | x , 1 , w \rangle \rightarrow | x , 1 - f ( x ) , w \rangle$. To query the oracle, one applies $\hat { f }$ to the current state. Grover's algorithm can be cast in terms of an oracle problem. The observation that this algorithm is optimal has been extended by using the method of polynomials [a4] to show that when no promise is made on the behaviour of the oracle, quantum computers are at most polynomially more efficient than classical computers.
An area where there are provable exponential gaps between the efficiency of quantum and classical computation occurs when communication resources are taken into consideration. This area is known as quantum communication complexity (introduced by A. Yao in 1993) and considers problems where two parties with quantum computers and a quantum channel between them (cf. Quantum information processing, science of) jointly compute a function of their respective inputs and wish to minimize the number of quantum bits communicated. The exponential gaps between quantum and classical communication complexity are so far confined to problems where the inputs to the function computed are constrained by a "promise" [a3]. The best known gap without a promise is a quadratic separation between classical and quantum protocols with bounded probability of error [a6]. Several research groups have developed techniques for proving lower bounds on quantum communication complexity, mostly variations of the log-rank lower bound also used in classical communication complexity. These results show that for some problems (for example, computing the inner product modulo two of bit strings known to the respective parties) there is little advantage to using quantum information processing.
References
| [a1] | J. Gruska, "Quantum computing" , McGraw-Hill (1999) |
| [a2] | M.A. Nielsen, I.L. Chuang, "Quantum computation and quantum information" , Cambridge Univ. Press (2000) |
| [a3] | R. Raz, "Exponential separation of quantum and classical communication complexity" , Proc. 31st Ann. ACM Symp. Theory of Computing (STOC'99) (1999) pp. 358–367 |
| [a4] | R. Beals, H. Buhrman, R. Cleve, M. Mosca, R. de Wolf, "Quantum lower bounds by polynomials" , Proc. 39th Ann. Symp. Foundations of Computer Sci. , IEEE Press (1998) pp. 352–361 |
| [a5] | Special focus issue, "Experimental proposals for quantum computation" Fortschr. Phys. , 48 (2000) pp. 767–1138 |
| [a6] | H. Buhrman, R. Cleve, A. Wigderson, "Quantum vs. classical communication and computation" , Proc. 30th Ann. ACM Symp. Theory of Computation , ACM Press (1998) pp. 63–68 |
Quantum computation, theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_computation,_theory_of&oldid=50147