Papperitz equation

An ordinary second-order Fuchsian linear differential equation having precisely three singular points:

$$ \tag{1 } w ^ {\prime\prime } + \left ( \frac{1 - \alpha - \alpha ^ \prime }{z-} a + \frac{1 - \beta - \beta ^ \prime }{z-} b + \frac{1- \gamma - \gamma ^ \prime }{z-} c \right ) w ^ \prime + $$

$$ + \left [ \frac{\alpha \alpha ^ \prime ( a- b)( a- c) }{z-} a + \frac{\beta \beta ^ \prime ( b- c)( b- a) }{z-} b\right . + $$

$$ + \left . \frac{\gamma \gamma ^ \prime ( c- a)( c- b) }{z-} c \right ] \frac{w}{(} z- a)( z- b)( z- c) = 0 , $$

$$ \alpha + \alpha ^ \prime + \beta + \beta ^ \prime + \gamma + \gamma ^ \prime = 1; $$

here $ a, b, c $ are pairwise distinct complex numbers, $ \alpha , \alpha ^ \prime $( $ \beta , \beta ^ \prime $ and $ \gamma , \gamma ^ \prime $) are the characteristic exponents at the singular point $ z= a $( respectively, $ z= b $ and $ z= c $). A Papperitz equation is uniquely determined by the assignment of the singular points and the characteristic exponents. In solving a Papperitz equation (1), use is made of Riemann's notation:

$$ w = P \left \{ \begin{array}{llll} a & b & c &{} \\ \alpha &\beta &\gamma & z \\ \alpha ^ \prime &\beta ^ \prime &\gamma ^ \prime &{} \\ \end{array} \right \} . $$

B. Riemann investigated [1] the problem of finding all many-valued functions $ w( z) $, analytic in the extended complex plane, which have the following properties:

a) the function $ w( z) $ has precisely three singular points $ a, b, c $;

b) any three of its branches are connected by a linear equation

$$ A _ {1} w _ {1} ( z) + A _ {2} w _ {2} ( z) + A _ {3} w _ {3} ( z) = 0 $$

with constant coefficients;

c) the function $ w( z) $ has the simplest singularities at the points $ a, b, c $; namely, in a neighbourhood of the point $ z= a $ there are two branches $ \widetilde{w} _ {1} ( z) $ and $ \widetilde{w} _ {2} ( z) $ satisfying

$$ \widetilde{w} _ {1} ( z) = \ ( z- a) ^ \alpha \phi _ {1} ( z) ,\ \ \widetilde{w} _ {2} ( z) = \ ( z- a) ^ {\alpha ^ \prime } \phi _ {2} ( z) , $$

where $ \phi _ {j} ( z) $ $ ( j = 1, 2) $ is holomorphic at $ z= a $; and analogously for $ b $ and $ c $.

Riemann, under certain additional assumptions on the numbers $ \alpha , \alpha ^ \prime \dots \gamma ^ \prime $, showed that all such functions can be expressed in terms of hypergeometric functions and that $ w( z) $ satisfies a linear second-order differential equation with rational coefficients, but did not write this equation out explicitly (see [1]). The equation in question, (1), was given by E. Papperitz [2]. It is also called the Riemann $ P $- equation, the Riemann equation in Papperitz's form and the Riemann equation, and its solutions are called $ P $- functions.

The basic properties of the solutions of a Papperitz equation are as follows.

1) A Papperitz equation is invariant under rational-linear transformations: If $ z _ {1} = ( Az + b)/( Cz + D) $ maps the points $ a, b, c $ to points $ a _ {1} , b _ {1} , c _ {1} $, then

$$ P \left \{ \begin{array}{llll} a & b & c &{} \\ \alpha &\beta &\gamma & z \\ \alpha ^ \prime &\beta ^ \prime &\gamma ^ \prime &{} \\ \end{array} \right \} = P \left \{ \begin{array}{llll} a _ {1} &b _ {1} &c _ {1} &{} \\ \alpha &\beta &\gamma &z _ {1} \\ \alpha ^ \prime &\beta ^ \prime &\gamma ^ \prime &{} \\ \end{array} \right \} . $$

2) The transformation

$$ \left ( z- \frac{a}{z-} b \right ) ^ {k} \left ( z- \frac{c}{z-} b \right ) ^ {l} w = \widetilde{w} $$

transforms a Papperitz equation into a Papperitz equation with the same singular points, but with different characteristic exponents:

$$ \left ( z- \frac{a}{z-} b \right ) ^ {k} \left ( z- \frac{c}{z-} b \right ) ^ {l} P \left \{ \begin{array}{llll} a & b & c &{} \\ \alpha &\beta &\gamma & z \\ \alpha ^ \prime &\beta ^ \prime &\gamma ^ \prime &{} \\ \end{array} \right \} = $$

$$ = \ P \left \{ \begin{array}{cccl} a & b & c &{} \\ \alpha + k &\beta - k- l &\gamma + l & z \\ \alpha ^ \prime + k &\beta ^ \prime - k- l &\gamma ^ \prime + l &{} \\ \end{array} \right \} . $$

3) The hypergeometric equation

$$ z( 1- z) w ^ {\prime\prime} + [ C - ( A+ B+ 1) z] w ^ \prime - ABw = 0 $$

is a special case of a Papperitz equation and it corresponds in Riemann's notation to

$$ P \left \{ \begin{array}{clcl} 0 &\infty & 1 &{} \\ 0 & A & 0 & z \\ 1- C & B &C- A- B &{} \\ \end{array} \right \} . $$

4) Each solution of a Papperitz equation can be expressed in terms of the hypergeometric function,

$$ \tag{2 } w( z) = \left ( z- \frac{a}{z-} b \right ) ^ \alpha \left ( z- \frac{c}{z-} b \right ) ^ \gamma \times $$

$$ \times F \left \{ \alpha + \beta + \gamma ; \alpha + \beta ^ \prime + \gamma ; 1 + \alpha - \alpha ^ \prime ; \frac{( z- a)( c- b) }{( z- b)( c- a) } \right \} $$

under the assumption that $ \alpha - \alpha ^ \prime $ is not a negative integer. If none of the differences $ \alpha - \alpha ^ \prime $, $ \beta - \beta ^ \prime $, $ \gamma - \gamma ^ \prime $ are integers, then interchanging in (2) the positions of $ \alpha $ and $ \alpha ^ \prime $ or of $ \gamma $ and $ \gamma ^ \prime $, four solutions of a Papperitz equation are obtained. In addition a Papperitz equation remains unchanged if the positions of the triples $ ( \alpha , \alpha ^ \prime , a) $, $ ( \beta , \beta ^ \prime , b) $, $ ( \gamma , \gamma ^ \prime , c) $ are rearranged; all these rearrangements provide 24 special solutions of a Papperitz equation (1), which were first obtained by E.E. Kummer [5].

References

[1]	B. Riemann, "Beiträge zur Theorie der durch Gauss'sche Reihe 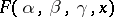darstellbare Functionen" , Gesammelte math. Werke , Dover, reprint (1953) pp. 67–85
[2]	E. Papperitz, "Ueber verwandte -Functionen" Math. Ann. , 25 (1885) pp. 212–221 MR1510304
[3]	E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 MR1424469 MR0595076 MR0178117 MR1519757 Zbl 0951.30002 Zbl 0108.26903 Zbl 0105.26901 Zbl 53.0180.04 Zbl 47.0190.17 Zbl 45.0433.02 Zbl 33.0390.01
[4]	V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) MR0100119
[5]	E.E. Kummer, "Ueber die hypergeometrische Reihe " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172