Wall group
An Abelian group associated with a ring with an involution which is an anti-isomorphism. In particular, it is defined for any group ring $ \mathbf Z [ \pi _ {1} ( X)] $,
where $ \pi _ {1} ( X) $
is the fundamental group of a space. If $ X $
is a Poincaré complex, then for a bordism class $ \alpha $
in $ \Omega _ {*} ( x, \nu ) $
there is an obstruction in this group to the existence of a simple homotopy equivalence in $ \alpha $.
This obstruction is called the Wall invariant, cf. [1].
Let $ R $ be a ring with an involution $ R \rightarrow R $ which is an anti-isomorphism, i.e. $ \overline{ {ab }}\; = \overline{ {ba }}\; $. If $ P $ is a left $ R $- module, then $ \mathop{\rm Hom} _ {R} ( P, R) $ is a left $ R $- module relative to the action $ ( af ) ( x) = f ( x) \overline{a}\; $, $ f \in \mathop{\rm Hom} _ {R} ( P, R) $, $ a \in R $, $ x \in P $. This module is denoted by $ P ^ {*} $. For a finitely-generated projective $ R $- module $ P $ there is an isomorphism $ P \rightarrow P ^ {**} $: $ x \mapsto ( f \mapsto \overline{ {f ( x) }}\; ) $, and one may identify $ P $ and $ P ^ {**} $ using this isomorphism.
A quadratic $ (- 1) ^ {k} $- form over a ring $ R $ with an involution is a pair $ ( P, \phi ) $, where $ P $ is a finitely-generated projective $ R $- module and $ \phi : P \rightarrow P ^ {*} $ is a homomorphism such that $ \phi = (- 1) ^ {k} \phi ^ {*} $. A morphism $ f: ( P, \phi ) \rightarrow ( Q, \psi ) $ of forms is a homomorphism $ f: P \rightarrow Q $ such that $ f ^ { * } \psi f = \phi $. If $ \phi $ is an isomorphism, then the form $ ( P, \phi ) $ is said to be non-degenerate. A Lagrange plane of a non-degenerate form is a direct summand $ L \subset P $ for which $ L = \mathop{\rm Ann} \phi ( L) $. If $ L \subset P $ is a direct summand such that $ L \subset \mathop{\rm Ann} \phi ( L) $, then $ L $ is called a subLagrange plane. Two Lagrange planes $ L, G $ of a form $ ( P, \phi ) $ are called complementary if $ L + G = P $ and $ L \cap G = \{ 0 \} $.
Let $ L $ be a projective $ R $- module. The non-degenerate $ (- 1) ^ {k} $- form
$$ H _ {(- 1) ^ {k} } ( L) = \ \left ( L \oplus L ^ {*} , \left (
is called Hamiltonian, and $ L, L ^ {*} \subset L \oplus L ^ {*} $ are called its complementary Lagrange planes. If $ L $ is a Lagrange plane of the form $ ( P, \phi ) $, then the form is isomorphic to the Hamiltonian form $ H _ {(- 1) ^ {k} } ( L) $. The choice of a Lagrange plane complementary to $ L $ is equivalent to the choice of an isomorphism $ ( P, \phi ) \rightarrow H _ {(- 1) ^ {k} } ( L) $, and this complementary plane can be identified with $ L ^ {*} $.
Let $ U _ {2k} ( R ) $ be the Abelian group generated by the equivalence classes (under isomorphism) of non-degenerate quadratic $ (- 1) ^ {k} $- forms $ ( P, \phi ) $ with the relations: 1) $ [( P, \phi )] + [( Q, \psi )] = [( P \oplus Q, \phi \oplus \psi )] $; and 2) $ [( P, \phi )] = 0 $ if $ P $ has a Lagrange plane. A triple $ ( H; F, L) $ consisting of a non-degenerate $ (- 1) ^ {k} $- form $ H $ and a pair of Lagrange planes is called a $ (- 1) ^ {k} $- formation. A formation is said to be trivial if $ F $ and $ L $ are complementary, and elementary if there exists a Lagrange plane of $ H $ which is complementary to both $ F $ and $ L $. The trivial formation $ ( H _ {(- 1) ^ {k} } ( G); G, G) $ is called Hamiltonian. By an isomorphism of formations, $ f: ( H; F, L) \rightarrow ( H _ {1} ; F _ {1} , L _ {1} ) $, one understands an isomorphism $ f: H \rightarrow H _ {1} $ of forms for which $ f ( F ) = F _ {1} $, $ f ( L) = L _ {1} $. Every trivial formation is isomorphic to the Hamiltonian one.
Let $ U _ {2k + 1 } ( R ) $ be the Abelian group generated by the equivalence classes (under isomorphism) of $ (- 1) ^ {k} $- formations with the following relations: a) $ [( H; F, L)] \oplus [( H _ {1} ; F _ {1} , L _ {1} )] = [( H \oplus H _ {1} ; F \oplus F _ {1} , L \oplus L _ {1} )] $; b) $ [( H; F, L)] = 0 $ if the formation is elementary or trivial.
The groups $ U _ {n} ( R) $ are called the Wall groups of the ring $ R $.
References
| [1] | C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970) MR0431216 Zbl 0219.57024 |
| [2] | A.A. Ranicki, "The algebraic theory of surgery I" Proc. London Math. Soc. , 40 : 1 (1980) pp. 87–192 MR0560997 MR0566491 Zbl 0471.57010 |
Comments
In the case of $ R = \mathbf Z [ \pi _ {1} ( X) ] $ and the Wall surgery obstruction invariant, the involution on $ R $ is given by $ g \mapsto w( g) g ^ {-} 1 $, $ g \in \pi _ {1} ( X) $, where the group homomorphism $ w : \pi _ {1} ( X) \rightarrow \{ 1, - 1 \} $ is given by the first Stiefel–Whitney class of the bundle $ \nu $ in the bordism class $ \Omega _ {*} ( X, \nu ) $.
The Wall groups $ U _ {n} ( R) $ are more often called $ L $- groups and denoted by $ L _ {n} ( R) $; their theory is referred to as $ L $- theory, which is much related to $ K $- theory. (Indeed, some authors speak of the $ K $- theory of forms, [a2].) The $ L $- groups are four-periodic, i.e. $ L _ {n} ( R) \simeq L _ {n+} 4 ( R) $. $ L $- groups can be defined in more general situations and there are a number of somewhat different varieties of $ L $- groups, cf. e.g. [a1], [a2].
References
| [a1] | A. Ranicki, "Lower 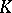 - and - and  -theory" , Cambridge Univ. Press (1992) MR1208729 -theory" , Cambridge Univ. Press (1992) MR1208729 |
| [a2] | A. Bak, "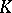 -theory of forms" , Princeton Univ. Press (1981) MR0632404 Zbl 0465.10013 -theory of forms" , Princeton Univ. Press (1981) MR0632404 Zbl 0465.10013 |
Wall group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wall_group&oldid=49167