Variety of groups
A class of all groups satisfying a fixed system of identity relations, or laws,
$$ v ( x _ {1} \dots x _ {n} ) = 1, $$
where $ v $ runs through some set $ V $ of group words, i.e. elements of the free group $ X $ with free generators $ x _ {1} \dots x _ {n} , . . . $. Just like any variety of algebraic systems (cf. Algebraic systems, variety of), a variety of groups can also be defined by the property of being closed under subsystems (subgroups), homomorphic images and Cartesian products. The smallest variety containing a given class $ \mathfrak C $ of groups is denoted by $ \mathop{\rm var} \mathfrak C $. Regarding the operations of intersection and union of varieties, defined by the formula
$$ \mathfrak U \lor \mathfrak V = \mathop{\rm var} ( \mathfrak U \cup \mathfrak V ), $$
varieties of groups form a complete modular, but not distributive, lattice. The product $ \mathfrak U \mathfrak V $ of two varieties $ \mathfrak U $ and $ \mathfrak V $ is defined as the variety of groups consisting of all groups $ G $ with a normal subgroup $ N \in \mathfrak U $ such that $ G/N \in \mathfrak V $. Any variety of groups other than the variety of trivial groups and the variety of all groups can be uniquely represented as a product of varieties of groups which cannot be split further.
Examples of varieties of groups: the variety $ \mathfrak A $ of all Abelian groups; the Burnside variety $ \mathfrak B _ {n} $ of all groups of exponent (index) $ n $, defined by the identity $ x ^ {n} = 1 $; the variety $ \mathfrak A _ {n} = \mathfrak B _ {n} \wedge \mathfrak A $; the variety $ \mathfrak N _ {c} $ of all nilpotent groups of class $ \leq c $; the variety $ \mathfrak A ^ {l} $ of all solvable groups of length $ \leq l $; in particular, if $ l = 2 $, $ \mathfrak A ^ {2} $ is the variety of metabelian groups.
Let $ {\mathcal P} $ be some property of groups. One says that a variety of groups $ \mathfrak V $ has the property $ {\mathcal P} $( locally) if each (finitely-generated) group in $ \mathfrak V $ has the property $ {\mathcal P} $. One says, in this exact sense, that the variety is nilpotent, locally nilpotent, locally finite, etc.
The properties of a solvable variety of groups $ \mathfrak V $ depend on $ \mathfrak V \wedge \mathfrak A ^ {2} $. Thus, if $ \mathfrak B \supseteq \mathfrak A ^ {2} $, then $ \mathfrak V \subseteq \mathfrak B _ {n} \mathfrak N _ {c} \mathfrak B _ {n} $ for certain suitable $ n $ and $ c $[2], [3]. The description of metabelian varieties of groups is reduced, to a large extent, to the description of locally finite varieties of groups: If a metabelian variety $ \mathfrak V $ is not locally finite, then
$$ \mathfrak B = \ \mathfrak B _ {1} \lor \mathfrak B _ {2} \lor \mathfrak B _ {3} , $$
where $ \mathfrak B _ {1} = \mathfrak A _ {m} \mathfrak A $, $ \mathfrak V _ {2} $ is uniquely representable as the union of a finite number of varieties of groups of the form $ \mathfrak N _ {c} \mathfrak A _ {k} \wedge \mathfrak A ^ {2} $, and $ \mathfrak V _ {3} $ is locally finite [4]. Certain locally finite metabelian varieties have been described — for example, varieties of $ p $- groups of class $ \leq p + 1 $( cf. [5]).
A variety of groups is said to be a Cross variety if it is generated by a finite group. Cross varieties of groups are locally finite. A variety of groups is said to be a near Cross variety if it is not Cross, but each of its proper subvarieties is Cross. The solvable near Cross varieties are exhausted by the varieties $ \mathfrak A $, $ \mathfrak A _ {p} ^ {2} $, $ \mathfrak A _ {p} \mathfrak A _ {q} \mathfrak A _ {r} $, $ \mathfrak A _ {p} \mathfrak T _ {q} $, where $ p, q, r $ are different prime numbers, $ \mathfrak T _ {q} = \mathfrak B _ {q} \wedge \mathfrak N _ {2} $ for odd $ q $ and $ \mathfrak T _ {2} = \mathfrak B _ {4} \wedge \mathfrak N _ {2} $[6]. There exist, however, other near Cross varieties; such varieties are contained, for example, in any variety $ \mathfrak K $ of all locally finite groups of exponent $ p \geq 5 $[7]. An important role in the study of locally finite varieties of groups is played by critical groups — groups not contained in the variety generated by all their proper subgroups and quotient groups. A Cross variety can contain only a finite number of non-isomorphic critical groups. All locally finite varieties are generated by their critical groups.
A variety of groups is said to be finitely based if it can be specified by a given finite number of identities. These include, for example, all Cross, nilpotent and metabelian varieties. It has been proved [8] that non-finitely based varieties of groups exist, and that the number of all varieties of groups has the power of the continuum. For examples of infinite independent systems of identities see [9]. A product of finitely-based varieties of groups is not necessarily finitely based; in particular, $ \mathfrak B _ {4} \mathfrak B _ {2} $ has no finite basis.
A variety of groups is a variety of Lie type if it is generated by its torsion-free nilpotent groups. If, in addition, the factors of the lower central series of the free groups of the variety are torsion-free groups, then the variety is said to be of Magnus type. The class of varieties of Lie type does not coincide with that of Magnus type; each of them is closed with respect to the operation of multiplication of varieties [10]. Examples of varieties of Magnus type include the variety of all groups, the varieties $ \mathfrak N _ {c} $, $ \mathfrak A ^ {n} $, and varieties obtained from $ \mathfrak N _ {c} $ by the application of a finite number of operations of intersection and multiplication [1].
References
| [1] | H. Neumann, "Varieties of groups" , Springer (1967) |
| [2] | M.I. Kargapolov, V.A. Churkin, "On varieties of solvable groups" Algebra and Logic , 10 : 6 (1971) pp. 359–398 Algebra i Logika , 10 : 6 (1971) pp. 651–657 |
| [3] | J.R.J. Groves, "On varieties of solvable groups II" Bull. Austr. Math. Soc. , 7 : 3 (1972) pp. 437–441 |
| [4] | R.A. Bryce, "Metabelian groups and varieties" Philos. Trans. Roy. Soc. London Ser. A , 266 (1970) pp. 281–355 |
| [5] | W. Brisley, "Varieties of metabelian 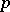 -groups of class -groups of class 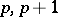 " J. Austr. Math. Soc. , 12 : 1 (1971) pp. 53–62 " J. Austr. Math. Soc. , 12 : 1 (1971) pp. 53–62 |
| [6] | A.Yu. Ol'shanskii, "Solvable just-non-Cross varieties of groups" Math. USSR Sb. , 14 : 1 (1971) pp. 115–129 Mat. Sb. , 85 : 1 (1971) pp. 115–131 |
| [7] | Yu.P. Razmyslov, "On Lie algebras satisfying the Engel condition" Algebra and Logic , 10 : 1 (1971) pp. 21–29 Algebra i Logika , 10 : 1 (1971) pp. 33–44 |
| [8] | A.Yu. Ol'shanskii, "On the problem of a finite basis of identities in groups" Math. USSR Izv. , 4 : 2 (1970) pp. 381–389 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 2 (1970) pp. 376–384 |
| [9] | S.I. Adyan, "The Burnside problem and identities in groups" , Springer (1979) (Translated from Russian) |
| [10] | A.L. Shmel'kin, "Wreath product of Lie algebras and their applications in the theory of groups" Proc. Moscow Math. Soc. , 29 (1973) pp. 239–252 Trudy Moskov. Mat. Obshch. , 29 (1973) pp. 247–260 |
| [11] | Yu.M. Gorchakov, "Commutator subgroups" Sib. Math. J. , 10 : 5 (1969) pp. 754–761 Sibirsk. Mat. Zh. , 10 : 5 (1969) pp. 1023–1033 |
Comments
The Oates–Powell theorem says that the variety generated by the finite groups is Cross. As a corollary it follows that the identities of finite groups admit a finite basis.
In [a1] the concept of varieties for a large class of algebraic structures was brought forward. The first systematic study of varieties of groups is [a2].
References
| [a1] | G. Birkhoff, "On the structure of abstract algebras" Proc. Cambridge Phil. Soc. , 31 (1935) pp. 433–454 |
| [a2] | B.H. Neumann, "Identical relations in groups I" Math. Ann. , 114 (1937) pp. 506–525 |
Variety of groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variety_of_groups&oldid=49129