Field operator
A linear weakly-continuous mapping $ f \rightarrow \phi _ {f} $,
$ f \in D ^ {L} ( \mathbf R ^ {4} ) $,
of the space $ D ^ {L} ( \mathbf R ^ {4} ) $
of basic functions $ f ( x) $,
$ x \in \mathbf R ^ {4} $,
that take values in a finite-dimensional vector space $ L $,
to the set of operators (generally speaking, unbounded) defined on a dense linear manifold $ D _ {0} \in H $
of some Hilbert space $ H $.
Here it is assumed that both in $ L $
and in $ H $
certain representations $ g \rightarrow T _ {g} $(
in $ L $)
and $ g \rightarrow U _ {g} $(
in $ H $),
$ g \in G $,
of the inhomogeneous Lorentz group $ G $
act in such a way that the equation
$$ \tag{* } U _ {g} \phi _ {f} U _ {g} ^ {-} 1 = \ \phi _ {\tau _ {g} f } ,\ \ g \in G,\ \ f \in D ^ {L} ( \mathbf R ^ {4} ), $$
holds, where
$$ ( \tau _ {g} f ) ( x) = \ T _ {g} f ( g ^ {-} 1 x),\ \ x \in \mathbf R ^ {4} . $$
Depending on the representation (scalar, vector, spinor, etc.) in $ L $, the field $ \{ {\phi _ {f} } : {f \in D ^ {L} ( \mathbf R ^ {4} ) } \} $ is called, respectively, scalar, vector or spinor. A family of field operators $ \{ {\phi _ {f} } : {f \in D ^ {L} ( \mathbf R ^ {4} ) } \} $ together with representations $ \{ {T _ {g} } : {g \in G } \} $ and $ \{ {U _ {g} } : {g \in G } \} $ for which condition (*) holds together with several general conditions (see [1]) is called a quantum (or quantized) field.
Aside from some models referring to the two-dimensional or three-dimensional world (see [2], [4]), one has constructed only (1983) simple examples of so-called free quantum fields [3].
References
| [1] | R. Jost, "The general theory of quantized fields" , Amer. Math. Soc. (1965) |
| [2] | B. Simon, "The 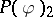 -Euclidean (quantum) field theory" , Princeton Univ. Press (1974) -Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [3] | N.N. Bogolyubov, D.V. Shirkov, "Introduction to the theory of quantized fields" , Interscience (1959) (Translated from Russian) |
| [4] | , Euclidean quantum field theory. The Markov approach , Moscow (1978) (In Russian; translated from English) |
Comments
References
| [a1] | P.J.M. Bongaarts, "The mathematical structure of free quantum fields. Gaussian fields" E.A. de Kerf (ed.) H.G.J. Pijls (ed.) , Proc. Seminar. Mathematical structures in field theory , CWI, Amsterdam (1987) pp. 1–50 |
Field operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Field_operator&oldid=46919