Carleman operator
A Carleman operator on the space $ L _ {2} ( X, \mu ) $
is an integral operator $ T $,
i.e., $ Tf ( x ) = \int {T ( x,y ) f ( y ) } {d \mu ( y ) } $
a.e. for $ f \in L _ {2} ( X, \mu ) $,
such that $ \| {T ( x, \cdot ) } \| _ {2} < \infty $
a.e. on $ X $.
Self-adjoint Carleman operators have generalized eigenfunction expansions (cf. Eigen function; Series expansion), which can be used in the study of linear elliptic operators, see [a1]. A general reference for Carleman operators on $ L _ {2} $-
spaces is [a2]. The notion of a Carleman operator has been extended in many directions. By replacing $ L _ {2} $
by an arbitrary Banach function space one obtains the so-called generalized Carleman operators (see [a3]) and by considering Bochner integrals (cf. Bochner integral) and abstract Banach spaces one is lead to the so-called Carleman and Korotkov operators on a Banach space ([a4]).
References
| [a1] | K. Maurin, "Methods of Hilbert spaces" , PWN (1967) |
| [a2] | P.R. Halmos, V.S. Sunder, "Bounded integral operators on 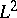 -spaces" , Ergebnisse der Mathematik und ihrer Grenzgebiete , 96 , Springer (1978) -spaces" , Ergebnisse der Mathematik und ihrer Grenzgebiete , 96 , Springer (1978) |
| [a3] | A.R. Schep, "Generalized Carleman operators" Indagationes Mathematicae , 42 (1980) pp. 49–59 |
| [a4] | N. Gretsky, J.J. Uhl, "Carleman and Korotkov operators on Banach spaces" Acta Sci. Math , 43 (1981) pp. 111–119 |
Carleman operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carleman_operator&oldid=46217