Adaptive stabilization

Suppose a dynamical input-output system modelling a process is given, i.e., a causal relationship between an input vector $ u ( \cdot ) $ and an output vector $ y ( \cdot ) $ described, for example, by a linear or non-linear difference or differential equation. Then the "classical" stabilization objective is to design another dynamical system, a feedback system, such that the output of the process is converted by the feedback system into the input of the process so that the closed-loop system achieves output stabilization, i.e., $ y ( t ) $ tends to zero as $ t $ tends to infinity.

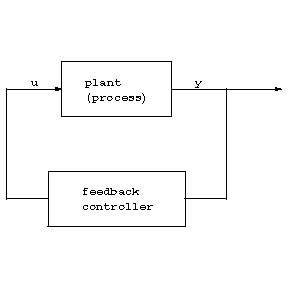
Figure: a110340a

However, the design of the feedback relies crucially on exact knowledge of the plant parameters. If the parameters of the plant are uncertain, change with time, or are even unknown and only structural information is available, then the only available information is the observed output. To achieve adaptive stabilization one designs (possibly by incorporating identification methods) an adaptive feedback system, that means it "adapts" (respectively, adjusts) its parameters according to the behaviour of the process, so that $ y ( t ) $ tends to zero as $ t $ tends to infinity. In other words, a single dynamical feedback system ensures stabilization of any process belonging to a class of systems. However, a precise and universal definition of adaptive control is still elusive.

Historical development.

Considerable research on adaptive control started in the early 1950s. The primary motivation was control of high-performance aircrafts which operate over a wide range of speeds and altitudes, with the controller having to change according to the rapidly changing operating conditions. However, only frequency domain methods were available at that time, and they did not suffice for solving adaptive control problems. Whilst in the 1960s and 1970s considerable control-theoretic contributions were made (the state space approach, stability theory, Lyapunov theory, the linear optimal regulator problem, Bellman's dynamic programming), a breakthrough was achieved in the late 1970s and early 1980s, when rigorous proofs for the stability of adaptive systems were presented. However, very soon a drawback was discovered. The existing adaptive controllers were not robust, but very sensitive to the presence of unmodelled dynamics. Since then, numerous authors have tackled and solved these problems, and adaptive control has matured.

Different adaptive concepts.

There is no common classification of adaptive concepts available in the literature. The reason is that numerous adaptive controllers consist of mixtures. An (incomplete) list of the dominating concepts is as follows.

Gain scheduling was one of the first adaptive concepts. It consists of a set of non-adaptive controllers $ C ( \theta _ {i} ) $, where $ \theta _ {i} $ parametrizes an operation condition. The adaptive controller switches between these $ C ( \theta _ {i} ) $ according to the region of operation that the plant is in. The problem is the transition between different operating points.

In model reference adaptive control, a reference model describing the input/output properties is given. The overall system consists of an inner (respectively, regulator) loop (i.e., plant and regulator) and an outer (respectively, adaptation) loop. The latter attempts to adjust the parameters of the regulator so that the model reference output is matched asymptotically.

In self-tuning adaptive control, the plant parameters are estimated by a recursive identification algorithm, and on the basis of these estimates a "classical" controller is chosen. The latter is also called the certainty equivalence principle.

Adaptive concepts are referred to as indirect or direct, depending upon whether the plant parameters are estimated first and then used to determine the controller, or the parameters are adjusted directly without intermediate calculations.

See the survey articles [a1], [a3], [a5], [a7] and the books [a2], [a4], [a6], [a8].

References

[a1]	K.J. Åström, "Adaptive feedback control" Proc. IEEE , 75 (1987) pp. 185–217
[a2]	K.J. Åström, B. Wittenmark, "Adaptive control" , Addison-Wesley (1989)
[a3]	A.L. Fradkov, "Continuous-time model reference adaptive systems, an east-west review" , Proc. IFAC Symp. Adaptive Control and Signal Processing (Grenoble, France, July 1992) (199?)
[a4]	P.A. Ioannou, J. Sun, "Robust adaptive control" , Prentice-Hall (1996)
[a5]	K.S. Narendra, "The maturing of adaptive control" P.V. Kokotović (ed.) , Foundations of Adaptive Control , Lecture Notes in Control and Information Systems , 160 , Springer (1991) pp. 3–36
[a6]	K.S. Narendra, A.M. Annaswamy, "Stable adaptive systems" , Prentice-Hall (1989)
[a7]	R. Ortega, T. Yu, "Robustness of adaptive controllers: a survey" Automatica , 25 (1989) pp. 651–678
[a8]	S. Sastry, M. Bodson, "Adaptive control: Stability, convergence and robustness" , Prentice-Hall (1989)