User:Maximilian Janisch/latexlist/Algebraic Groups/Steinberg module
Let $G = GL _ { n } ( F _ { q } )$, the group of all invertible $( n \times n )$-matrices over the finite field $F _ { q }$ with $h$ elements and characteristic $D$, let $B$ be the subgroup of all superdiagonal elements, let $r$ be the subgroup of elements of $B$ whose diagonal entries are all $1$, and let $v$ be the subgroup of permutation matrices. In the group algebra $k [ G ]$ of $k$ over any field $k$ of characteristic $0$ or $D$, the element
\begin{equation} e = \frac { | U | } { | G | } ( \sum _ { b \in B } b ) ( \sum _ { w \in W } \operatorname { sign } ( w ) w ) \end{equation}
is an idempotent, called the Steinberg idempotent, and the $k$-module that it generates in $k [ G ]$ by right multiplication is called the Steinberg module (see [a8]) and is commonly denoted $St$ (as are all modules isomorphic to it). A similar construction holds for any finite group $k$ of Lie type (and for any $B N$-pair, which is an axiomatic generalization due to J. Tits) defined over a field of characteristic $D$ with $B$ replaced by a Borel subgroup (which is a certain kind of solvable subgroup), $r$ by a maximal unipotent subgroup (cf. Unipotent group) of $B$ (which is also a Sylow $D$-subgroup of $k$; cf. also Sylow subgroup; $D$-group) and $v$ by the corresponding Weyl group. $St$ is always irreducible and it has $\{ e u : u \in U \}$ as a basis, so that its dimension is $| U |$ (see [a8]). Its character values are given as follows [a3]. If $x \in G$ has order prime to $D$, then $\chi ( x )$ equals, up to a sign which can be determined, the order of a Sylow $D$-subgroup of the centralizer of $\pi$; otherwise it equals $0$.
In case the characteristic of $k$ equals $D$, $St$ has the following further properties [a5]. It is the only module (for $k$) which is both irreducible and projective. As an irreducible module it is the largest (in dimension), and as a projective module it is the smallest since it is a tensor factor of every projective module. It follows that it is also self-dual and that every projective module is also injective and vice versa. Because of these remarkable properties, $St$ plays a prominent role in ongoing work in the still (2000) unresolved problem of determining all of the irreducible $k$-modules (with characteristic $k$ still equal to $D$), or equivalently, as it turns out, of determining all of the irreducible rational $\overline { C }$-modules, where $\overline { C }$ is the algebraic group obtained from $k$ by replacing $F _ { q }$ by its algebraic closure $F _ { q }$, i.e., where $\overline { C }$ is any simple affine algebraic group of characteristic $D$ (see [a6]). This equivalence comes from the fact that every irreducible $k$-module extends to a rational $\overline { C }$-module. In particular, $St$ extends to the $\overline { C }$-module with highest weight $q - 1$ times the sum of the fundamental weights, which is accordingly also denoted $St$, or $S t _ { q }$ since there is one such $\overline { C }$-module for each $q = p , p ^ { 2 } , p ^ { 3 } , . .$. These modules are ubiquitous in the module theory of $\overline { C }$ and figure prominently, for example, in the proofs of many cohomological vanishing theorems and in W. Haboush's proof of the Mumford hypothesis (see [a4]).
Back in the finite case, some other constructions of $St$, with the characteristic of $k$ now equal to $0$, are as follows. According to C.W. Curtis [a2]
\begin{equation} St = \sum _ { P } \pm 1 _ { F } ^ { G } \end{equation}
in which $P$ runs through the $2 ^ { r }$ ($N$ equal to the rank of $k$) (parabolic) subgroups of $k$ containing $B$, $1 \frac { G } { P }$ is the $k$-module induced by the trivial $P$-module, and the $-$ or  is used according as the rank $r _ { f }$ of $P$ is even or odd. For $G = GL _ { n } ( F _ { q } )$, for example, there is one $P$ for each solution of $n = a _ { 1 } + \ldots + a _ { s }$ ($1 \leq s \leq n$, each $a _ { i } \geq 1$); it consists of all of the elements of $k$ that are superdiagonal in the corresponding block matrix form. A third construction, due to L. Solomon and Tits [a7], yields $St$ as the top homology space $H _ { r - 1 } ( C )$ for the Tits simplicial complex or Tits building $C$ of $k$, formed as follows: corresponding to each parabolic subgroup $P$ there exists an $( r - r _ { P } - 1 )$-simplex $S _ { F }$ in $C$, and $S _ { F }$ is a facet of $S _ { 0 }$ just when $P$ contains $8$. These three constructions are, in fact, closely related to each other (see [a9]). In particular, the idempotent $E$ used at the start can be identified with an $( r - 1 )$-sphere in the Tits building, the sum over $v$ corresponding to a decomposition of the sphere into simplexes: in the usual action of $v$ on $S ^ { r - 1 } \subset R ^ { r }$ the reflecting hyperplanes divide $s ^ { \gamma } - 1$ into $| W |$ oriented spherical simplexes, each of which is a fundamental domain for $v$. Finally, $St$ has a simple presentation (as a linear space). It is generated by the Borel subgroups of $k$ subject only to the relations that for every parabolic subgroup of rank $1$ the sum of the Borel subgroups that it contains is $0$.
is used according as the rank $r _ { f }$ of $P$ is even or odd. For $G = GL _ { n } ( F _ { q } )$, for example, there is one $P$ for each solution of $n = a _ { 1 } + \ldots + a _ { s }$ ($1 \leq s \leq n$, each $a _ { i } \geq 1$); it consists of all of the elements of $k$ that are superdiagonal in the corresponding block matrix form. A third construction, due to L. Solomon and Tits [a7], yields $St$ as the top homology space $H _ { r - 1 } ( C )$ for the Tits simplicial complex or Tits building $C$ of $k$, formed as follows: corresponding to each parabolic subgroup $P$ there exists an $( r - r _ { P } - 1 )$-simplex $S _ { F }$ in $C$, and $S _ { F }$ is a facet of $S _ { 0 }$ just when $P$ contains $8$. These three constructions are, in fact, closely related to each other (see [a9]). In particular, the idempotent $E$ used at the start can be identified with an $( r - 1 )$-sphere in the Tits building, the sum over $v$ corresponding to a decomposition of the sphere into simplexes: in the usual action of $v$ on $S ^ { r - 1 } \subset R ^ { r }$ the reflecting hyperplanes divide $s ^ { \gamma } - 1$ into $| W |$ oriented spherical simplexes, each of which is a fundamental domain for $v$. Finally, $St$ has a simple presentation (as a linear space). It is generated by the Borel subgroups of $k$ subject only to the relations that for every parabolic subgroup of rank $1$ the sum of the Borel subgroups that it contains is $0$.
There are also infinite-dimensional versions of the above constructions, usually for reductive Lie groups — real, complex or $D$-adic — such as 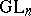 . The $D$-adic case most closely resembles the finite case. There, the affine Weyl group and a certain compact-open subgroup, called an Iwahori subgroup, come into play (in place of $v$ and $B$), and the three constructions agree. In [a1] several types of buildings, Curtis' formula and the Steinberg idempotent, in the guise of a homology cycle, all appear. In the infinite case the constructed object is sometimes called the Steinberg representation, sometimes the special representation.
. The $D$-adic case most closely resembles the finite case. There, the affine Weyl group and a certain compact-open subgroup, called an Iwahori subgroup, come into play (in place of $v$ and $B$), and the three constructions agree. In [a1] several types of buildings, Curtis' formula and the Steinberg idempotent, in the guise of a homology cycle, all appear. In the infinite case the constructed object is sometimes called the Steinberg representation, sometimes the special representation.
References [a5] and [a9] are essays on $St$.
References
| [a1] | A. Borel, J-P. Serre, "Cohomologie d'immeubles et de groupes $5$-arithmétiques" Topology , 15 (1976) pp. 211–232 MR447474 |
| [a2] | C.W. Curtis, "The Steinberg character of a finite group with $B N$-pair" J. Algebra , 4 (1966) pp. 433–441 MR201524 |
| [a3] | C.W. Curtis, G.I. Lehrer, J. Tits, "Spherical buildings and the character of the Steinberg representation" Invent. Math. , 58 (1980) pp. 201–220 MR0571572 Zbl 0435.20024 |
| [a4] | W. Haboush, "Reductive groups are geometrically reductive" Ann. of Math. , 102 (1975) pp. 67–83 MR0382294 Zbl 0316.14016 |
| [a5] | J.E. Humphreys, "The Steinberg representation" Bull. Amer. Math. Soc. (N.S.) , 16 (1987) pp. 237–263 MR0876960 Zbl 0627.20024 |
| [a6] | J.C. Jantzen, "Representations of algebraic groups" , Acad. Press (1987) MR0899071 Zbl 0654.20039 |
| [a7] | L. Solomon, "The Steinberg character of a finite group with $B N$-pair" , Theory of Finite Groups (Harvard Symp.) , Benjamin (1969) pp. 213–221 |
| [a8] | R. Steinberg, "Prime power representations of finite linear groups II" Canad. J. Math. , 9 (1957) pp. 347–351 MR0087659 Zbl 0079.25601 |
| [a9] | R. Steinberg, "Collected Papers" , Amer. Math. Soc. (1997) pp. 580–586 Zbl 0878.20002 |
Maximilian Janisch/latexlist/Algebraic Groups/Steinberg module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/Algebraic_Groups/Steinberg_module&oldid=44061