Fisher z-distribution
A continuous probability distribution on the real line with density
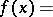 |
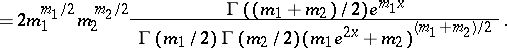 |
The parameters 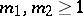 are called the degrees of freedom. The characteristic function has the form
are called the degrees of freedom. The characteristic function has the form
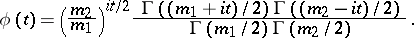 |
The mathematical expectation and the variance are equal to 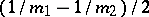 and
and 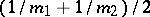 , respectively.
, respectively.
If the random variable  has the Fisher
has the Fisher  -distribution with
-distribution with 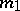 and
and  degrees of freedom, then the quantity
degrees of freedom, then the quantity 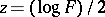 has the Fisher
has the Fisher  -distribution with
-distribution with 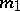 and
and 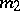 degrees of freedom. Along with the Fisher
degrees of freedom. Along with the Fisher 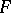 -distribution, known as the distribution of the dispersion proportion, the Fisher
-distribution, known as the distribution of the dispersion proportion, the Fisher  -distribution was originally introduced in the analysis of variance by R.A. Fisher (1924). His intention was that the
-distribution was originally introduced in the analysis of variance by R.A. Fisher (1924). His intention was that the  -distribution should be the basic distribution for testing statistical hypotheses in the analysis of variance. The Fisher
-distribution should be the basic distribution for testing statistical hypotheses in the analysis of variance. The Fisher  -distribution was tabulated at the same time, and the first research was concerned with the statistic
-distribution was tabulated at the same time, and the first research was concerned with the statistic  , although in modern mathematical statistics one uses the simpler statistic
, although in modern mathematical statistics one uses the simpler statistic 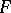 .
.
References
| [1] | R.A. Fisher, "On a distribution yielding the error functions of several well-known statistics" , Proc. Internat. Congress mathematicians (Toronto 1924) , 2 , Univ. Toronto Press (1928) pp. 805–813 |
Comments
The dispersion proportion is also called the variance ratio.
Fisher z-distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fisher_z-distribution&oldid=43081