Lebesgue integral

2020 Mathematics Subject Classification: Primary: 28A25 [MSN][ZBL]

The most important generalization of the concept of an integral. Let $(X,\mu)$ be a space with a non-negative complete countably-additive measure $\mu$ (cf. Countably-additive set function; Measure space), where $\mu(X)<\infty$. A simple function is a measurable function $g:X\to\mathbb R$ that takes at most a countable set of values: $g(x)=y_n$, $y_n\ne y_k$ for $n\ne k$, if $x\in X_n$, $\bigcup\limits_{n=1}^{\infty}X_n=X$. A simple function $g$ is said to be summable if the series \begin{equation} \sum\limits_{n=1}^{\infty}y_n\mu(X_n) \end{equation} converges absolutely (cf. Absolutely convergent series); the sum of this series is the Lebesgue integral \begin{equation} \int\limits_X g\ d\mu. \end{equation} A function $f:X\to\mathbb R$ is summable on $X$ (the notation is $f\in L_1(X,\mu)$) if there is a sequence of simple summable functions $g_n$ uniformly convergent (cf. Uniform convergence) to $f$ on a set of full measure, and if the limit \begin{equation} \lim\limits_{n\to\infty}\int\limits_X g_n\ d\mu = I \end{equation} is finite. The number $I$ is the Lebesgue integral \begin{equation} \int\limits_X f\ d\mu. \end{equation}

This is well-defined: the limit $l$ exists and does not depend on the choice of the sequence $g_n$. If $f\in L_1(X,\mu)$, then $f$ is a measurable almost-everywhere finite function on $X$. The Lebesgue integral is a linear non-negative functional on $L_1(X,\mu)$ with the following properties:

1) if $L_1(X,\mu)$ and if

\begin{equation}\mu\{x\in X:\ f(x)\neq h(x)\}=0,\end{equation}

then $h\in L_1(X,\mu)$ and

\begin{equation}\int\limits_X f\ d\mu=\int\limits_X g\ d\mu\end{equation}

2) if $f\in L_1(X,\mu)$, then $|f|\in L_1(X,\mu)$ and

\begin{equation}\left|\int\limits_X f\ d\mu\right|\leq\int\limits_X |f|\ d\mu\end{equation}

3) if $f\in L_1(X,\mu),|h|\leq f$ and $h$ is measurable, then $h\in L_1(X,\mu)$ and

\begin{equation}\left|\int\limits_X h\ d\mu\right|\leq\int\limits_X f\ d\mu\end{equation}

4) if $m\leq f\leq M$ and $f$ is measurable, then $f\in L_1(X,\mu)$ and

\begin{equation}m\mu X\leq\int\limits_X f\ d\mu\leq M\mu X\end{equation}

In the case when $\mu X=+\infty$ and $X=\cup_{n=1}^\infty X_n,\mu X_n<+\infty$ the Lebesgue integral is defined as

\begin{equation}\lim\limits_{n\to\infty}\int\limits_{E_n} f\ du\end{equation}

under the condition that this limit exists and is finite for any sequence $E_n$ such that $\mu E_n<+\infty,E_n\subset E_{n+1},\cup_{n=1}^\infty E_n=X$. In this case the properties 1), 2), 3) are preserved, but condition 4) is violated.

For the transition to the limit under the Lebesgue integral sign see Lebesgue theorem.

If $A$ is a measurable set in $X$, then the Lebesgue integral

\begin{equation}\int\limits_A f\ d\mu\end{equation}

is defined either as above, by replacing $X$ by $A$, or as

\begin{equation}\int\limits_X f\chi_A\ d\mu\end{equation}

where $\chi_A$ is the characteristic function of $A$ these definitions are equivalent. If $f\in L_1(A,\mu)$, then $f\in L_1(A_1,\mu)$ for any measurable $A_1\subset A$.

If

\begin{equation}A=\bigcup_{n=1}^\infty A_n\end{equation}

if $A$ is measurable for every $n$, if

\begin{equation}A_n\cap A_k\ \text{for}\ n\neq k\end{equation}

and if $f\in L_1(A,\mu)$ then

\begin{equation}\int\limits_A f\ d\mu=\sum_{n=1}^\infty \int\limits_{A_n} f\ d\mu\end{equation}

Conversely, if under these conditions on $A_n$ one has $f\in L_1(A,\mu)$ for every $n$ and if $\sum_{n=1}^\infty\int\limits_{A_n} |f|\ d\mu$ then $f\in L_1(A,\mu)$ and the previous equality is true ($\sigma$-additivity of the Lebesgue integral).

The function of sets $A\subset X$ given by $F(A)=\int\limits_A f\ d\mu$ is absolutely continuous with respect to $\mu$ (cf. Absolute continuity); if $f\geq 0$, then $F$ is a non-negative measure that is absolutely continuous with respect to $\mu$. The converse assertion is the Radon–Nikodým theorem.

For functions 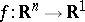the name "Lebesgue integral" is applied to the corresponding functional if the measure 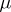is the Lebesgue measure; here, the set of summable functions is denoted simply by 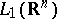, and the integral by

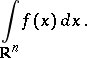For other measures this functional is called a Lebesgue–Stieltjes integral.

If 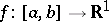, 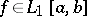and if 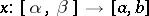is a non-decreasing absolutely continuous function, then

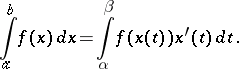If 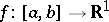, 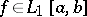and if 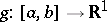is monotone on 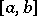, then 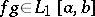and there is a point 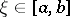such that

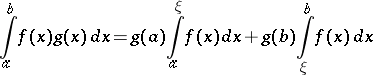(the second mean-value theorem).

In 1902 H. Lebesgue gave (see [Le]) a definition of the integral for 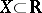and measure 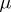equal to the Lebesgue measure. He constructed simple functions that uniformly approximate almost-everywhere on a set 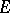of finite measure a measurable non-negative function 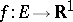, and proved the existence of a common limit (finite or infinite) of the integrals of these simple functions as they tend to 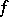. The Lebesgue integral is a basis for various generalizations of the concept of an integral. As N.N. Luzin remarked [Lu], property 2), called absolute integrability, distinguishes the Lebesgue integral for 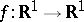from all possible generalized integrals.

References

[Le]	H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928) MR2857993 Zbl 54.0257.01
[Lu]	N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1915) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212)
[KF]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) MR1025126 MR0708717 MR0630899 MR0435771 MR0377444 MR0234241 MR0215962 MR0118796 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801

Comments

For other generalizations of the notion of an integral see -integral; Bochner integral; Boks integral; Burkill integral; Daniell integral; Darboux sum; Denjoy integral; Kolmogorov integral; Perron integral; Perron–Stieltjes integral; Pettis integral; Radon integral; Stieltjes integral; Strong integral; Wiener integral. See also, of course, Riemann integral. See also Double integral; Improper integral; Fubini theorem (on changing the order of integration).

References

[H]	P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802
[P]	I.N. Pesin, "Classical and modern integration theories" , Acad. Press (1970) (Translated from Russian) MR0264015 Zbl 0206.06401
[S]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) MR0167578 Zbl 1196.28001 Zbl 0017.30004 Zbl 63.0183.05
[Ro]	H.L. Royden, "Real analysis", Macmillan (1968)
[Ru]	W. Rudin, "Real and complex analysis" , McGraw-Hill (1978) pp. 24 MR1736644 MR1645547 MR0924157 MR0850722 MR0662565 MR0344043 MR0210528 Zbl 1038.00002 Zbl 0954.26001 Zbl 0925.00005 Zbl 0613.26001 Zbl 0925.00003 Zbl 0278.26001 Zbl 0142.01701
[HS]	E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) MR0188387 Zbl 0137.03202