Latin rectangle
A rectangular matrix of dimension  ,
,  , each row of which is a permutation (without repetitions) of the elements of a set
, each row of which is a permutation (without repetitions) of the elements of a set  consisting of
consisting of  elements, and in the columns each element occurs at most once. For
elements, and in the columns each element occurs at most once. For  a Latin rectangle is a Latin square of order
a Latin rectangle is a Latin square of order  . Usually
. Usually  , and one says that the Latin rectangle is constructed on the set
, and one says that the Latin rectangle is constructed on the set  .
.
A Latin rectangle exists for any natural numbers  and
and  ,
, 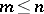 . An example of a Latin rectangle is a matrix with first row
. An example of a Latin rectangle is a matrix with first row  and where any subsequent row is obtained from the previous row by a cyclic shift by one place. A Latin rectangle of dimension
and where any subsequent row is obtained from the previous row by a cyclic shift by one place. A Latin rectangle of dimension  ,
, 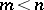 , can always be completed to a Latin square of order
, can always be completed to a Latin square of order  in such a way that the first
in such a way that the first  rows of the Latin square are the same as those of the Latin rectangle.
rows of the Latin square are the same as those of the Latin rectangle.
For the number  of Latin rectangles of dimension
of Latin rectangles of dimension  one has the following lower bound:
one has the following lower bound:
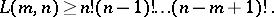 |
A Latin rectangle is said to be normalized if its first row is 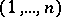 . The number
. The number 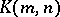 of normalized Latin rectangles is connected with
of normalized Latin rectangles is connected with 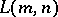 by the relation
by the relation
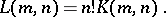 |
The calculation of 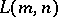 for
for  and 3 is connected with the following classical combinatorial problems: the problem of the number of derangements (see also Inversion (in combinatorics)) and the married-couples problem. Thus, the number of derangements
and 3 is connected with the following classical combinatorial problems: the problem of the number of derangements (see also Inversion (in combinatorics)) and the married-couples problem. Thus, the number of derangements 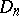 equals
equals  , and the number of arrangements
, and the number of arrangements 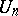 in the married-couples problem is the number of Latin rectangles of dimension
in the married-couples problem is the number of Latin rectangles of dimension 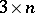 with first two rows
with first two rows
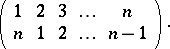 |
For 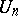 one has the formulas
one has the formulas
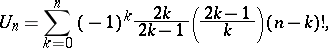 |
 |
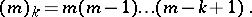 |
The number 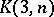 can be expressed in terms of
can be expressed in terms of  and
and 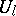 :
:
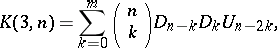 |
where 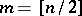 ,
, 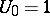 . One also has the following asymptotic expansion:
. One also has the following asymptotic expansion:
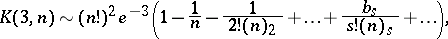 |
where 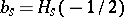 ,
,  being the Hermite polynomials. It is also known that
being the Hermite polynomials. It is also known that
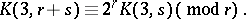 |
The problem of enumerating Latin rectangles having more than three rows is unsolved (1982). For 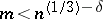 , where
, where 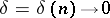 such that
such that 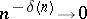 , the following asymptotic behaviour holds:
, the following asymptotic behaviour holds:
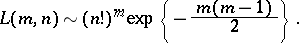 |
Certain concepts and theorems connected with Latin squares can be extended to Latin rectangles. Thus, two Latin rectangles 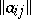 and
and 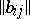 of dimension
of dimension 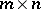 are said to be orthogonal if all pairs of the form
are said to be orthogonal if all pairs of the form  are distinct. A set of Latin rectangles in which any two of them are orthogonal has at most
are distinct. A set of Latin rectangles in which any two of them are orthogonal has at most 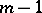 Latin rectangles.
Latin rectangles.
The term "Latin rectangle" is often used in a more general sense: A generalized Latin rectangle of dimension 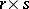 , constructed on a set
, constructed on a set 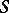 consisting of
consisting of  elements, is a matrix of dimension
elements, is a matrix of dimension 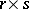 with elements from
with elements from 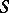 that occur at most once in each row and column. A (generalized) Latin rectangle of dimension
that occur at most once in each row and column. A (generalized) Latin rectangle of dimension  constructed on
constructed on  symbols can be extended to a Latin square of order
symbols can be extended to a Latin square of order  if and only if each symbol occurs at least
if and only if each symbol occurs at least 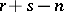 times in the Latin rectangle.
times in the Latin rectangle.
See also the references to Latin square.
References
| [1] | J. Riordan, "An introduction to combinatorial analysis" , Wiley (1967) |
Comments
The married-couples problem (or problème des ménages) asks for the number of ways of seating  married couples at a circular table with men and women alternating and so that no wife sits next to her husband. The number of solutions is
married couples at a circular table with men and women alternating and so that no wife sits next to her husband. The number of solutions is 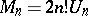 , where
, where 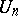 is called the
is called the  -th ménage number. The number
-th ménage number. The number  is equal to the number of permutations
is equal to the number of permutations 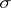 of
of  such that
such that 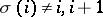 for all
for all 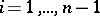 and
and 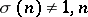 .
.
Latin rectangle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Latin_rectangle&oldid=39892