*-regular ring
From Encyclopedia of Mathematics
A regular ring (in the sense of von Neumann) admitting an involutory anti-automorphism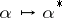 
such that 
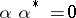implies 
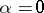. An idempotent 
of a 
-regular ring is called a projector if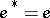 
. Every left (right) ideal of a 
-regular ring is generated by a unique projector. One can thus speak of the lattice of projectors of a 
-regular ring. If this lattice is complete, then it is a continuous geometry. A complemented modular lattice (cf. also Lattice with complements) having a homogeneous basis 
, where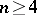 
, is an ortho-complemented lattice if and only if it is isomorphic to the lattice of projectors of some 
-regular ring.
References
| [1] | L.A. Skornyakov, "Complemented modular lattices and regular rings" , Oliver & Boyd (1964) (Translated from Russian) |
| [2] | S.K. Berberian, "Baer  -rings" , Springer (1972) |
| [3] | I. Kaplansky, "Rings of operators" , Benjamin (1968) |
How to Cite This Entry:
*-regular ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-regular_ring&oldid=39393
*-regular ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-regular_ring&oldid=39393
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article