Cauchy filter
A filter $\mathfrak{F}$ on a uniform space $X$ such that for any entourage $V$ of the uniform structure of $X$ there exists a set which is $V$-small and belongs to $\mathfrak{F}$. In other words, a Cauchy filter is a filter which contains arbitrarily small sets in a uniform space $X$. The concept is a generalization of the concept of a Cauchy sequence in metric spaces.
Every convergent filter (cf. Limit) is a Cauchy filter. Every filter which is finer than a Cauchy filter is also a Cauchy filter. The image of a Cauchy filterbase under a uniformly-continuous mapping is again a Cauchy filterbase. A uniform space in which every Cauchy filter is convergent is a complete space.
References
| [1] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) pp. Chapt. II: Uniform structures (Translated from French) |
Comments
A Cauchy filterbase (or Cauchy $d$-filterbase) is a filterbase 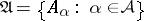 in a metric space
in a metric space 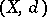 such that for every
such that for every 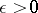 there is some
there is some  for which
for which 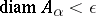 (cf. [a1]).
(cf. [a1]).
A filterbase in a space 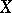 is a family
is a family 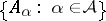 of subsets of
of subsets of 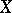 with the properties: 1)
with the properties: 1) 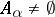 for all
for all  ; and 2) for all
; and 2) for all  there is a
there is a  such that
such that 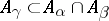 (see also Filter).
(see also Filter).
References
| [a1] | J. Dugundji, "Topology" , Allyn & Bacon (1978) |
Cauchy filter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_filter&oldid=38766