Sum function of a function
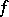
The function of 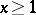 that denotes the sum of the values
that denotes the sum of the values 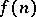 of the function
of the function 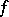 on the set of natural numbers
on the set of natural numbers 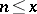 ,
,  . Sum functions are one of the basic means of expressing various properties of sequences of numbers.
. Sum functions are one of the basic means of expressing various properties of sequences of numbers.
Examples of sum functions: the number of prime numbers 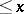 ;
; 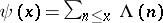 — the Chebyshev function; the number of divisors of all
— the Chebyshev function; the number of divisors of all 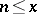 , etc. (see [1], [2]).
, etc. (see [1], [2]).
The basic problem is to find as accurate as possible an expression of the sum function, and for a sum function which does not have asymptotics, to find the best estimate of its modulus for large values of  .
.
The Cauchy integral theorem and Dirichlet series of the form
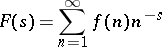 |
form the basis of the analytic methods of studying sum functions. If such a series converges absolutely for  , then for a non-integer
, then for a non-integer  , and
, and 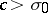 , the identity
, the identity
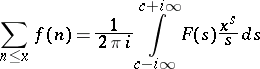 |
holds; a corresponding estimate of the sum function of 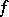 is obtained from this by analytic continuation of
is obtained from this by analytic continuation of  by shifting the integration path to the left to a certain
by shifting the integration path to the left to a certain 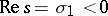 and estimating the integral along the new path. If
and estimating the integral along the new path. If 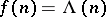 , for example, the integration can be shifted to
, for example, the integration can be shifted to 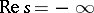 , which gives the Riemann–von Mangoldt formula for
, which gives the Riemann–von Mangoldt formula for 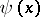 . Of the common applications of the method, the following theorem is known.
. Of the common applications of the method, the following theorem is known.
Assumptions:
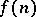 ,
,  are complex numbers,
are complex numbers,  ,
, 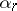 ,
, 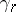 are real numbers,
are real numbers,  ,
,  are positive numbers,
are positive numbers, 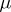 and
and  are integers
are integers 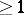 ,
,  is the gamma-function, and
is the gamma-function, and 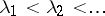 .
.
1) For any 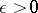 ,
, 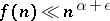 ;
;
2) the function
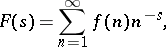 |
defined for 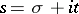 ,
, 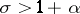 , is meromorphic in the whole plane, and has a finite number of poles in the strip
, is meromorphic in the whole plane, and has a finite number of poles in the strip 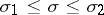 ;
;
3) the series 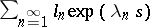 converges absolutely when
converges absolutely when  ;
;
4) for 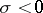 ,
,
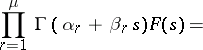 |
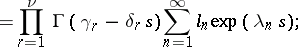 |
5) 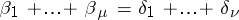 ;
;
6) if one assumes that
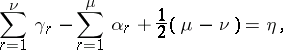 |
then 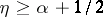 .
.
For a fixed strip 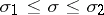 there is a constant
there is a constant 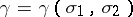 such that for
such that for 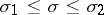 and large
and large 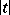 the estimate
the estimate  holds.
holds.
Conclusion.
For any 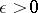 ,
,
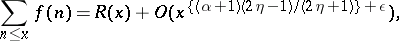 |
where 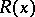 is the sum of the residues of the function
is the sum of the residues of the function 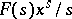 over all its poles in the strip
over all its poles in the strip
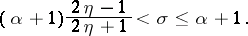 |
References
| [1] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) |
| [2] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1) |
Comments
The Riemann–von Mangoldt formula, or von Mangoldt formula, for 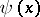 ,
, 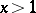 , is
, is
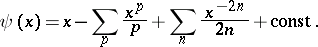 |
This is von Mangoldt's reformulation of Riemann's main formula
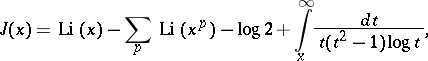 |
where 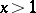 , the
, the 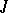 -function is
-function is
 |
and 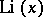 is the logarithmic integral
is the logarithmic integral
 |
References
| [a1] | H.M. Edwards, "Riemann's zeta function" , Acad. Press (1974) pp. Chapt. 3 |
Sum function of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sum_function_of_a_function&oldid=35832