Normal number

2020 Mathematics Subject Classification: Primary: 11K16 [MSN][ZBL]

A real number 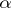, , 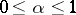having the following property: For every natural number , any given -tuple 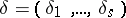consisting of the symbols 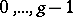appears with asymptotic frequency 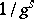in the sequence

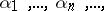(1)

obtained from the expansion of 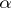in an infinite fraction in base ,

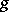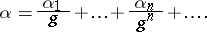In more detail, let 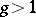be a natural number and let

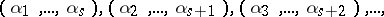(2)

be the infinite sequence of -tuples corresponding to (1). Let 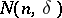denote the number of occurrences of the tuple 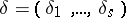among the first tuples of (2). The number

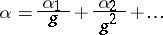is said to be normal if for any number and any given -tuple 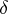consisting of the symbols ,

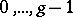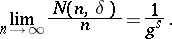The concept of a normal number was introduced for by E. Borel (see [B], [B2], p. 197). He called a real number 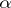weakly normal to the base 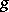if

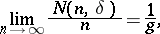where 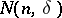is the number of occurrences of 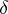, , 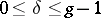among the first terms of the sequences 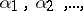and normal if are weakly normal to the bases 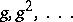. He also showed that for a normal number

for any and any given -tuple . Later it was proved (see [Pi], [NZ], and also [Po]) that the last relation is equivalent to Borel's definition of a normal number.

A number 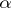is called absolutely normal if it is normal with respect to every base 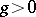. The existence of normal and absolutely-normal numbers was established by Borel on the basis of measure theory. The construction of normal numbers in an explicit form was first achieved in [C]. Earlier (see [S], [L]) an effective procedure for constructing normal numbers was indicated. For other methods for constructing normal numbers and for connections between the concepts of normality and randomness see [Po].

Uniform distribution of the fractional parts 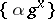, 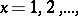on the interval 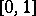is equivalent to being normal.

References

[B]	E. Borel, "Les probabilités dénombrables et leurs applications arithmétiques" Rend. Circ. Math. Palermo , 27 (1909) pp. 247–271 Zbl 40.0283.01
[B2]	E. Borel, "Leçons sur la théorie des fonctions" , Gauthier-Villars (1928) MR0033328 Zbl 54.0327.02
[Pi]	S. Pillai, "On normal numbers" Proc. Indian Acad. Sci. Sect. A , 12 (1940) pp. 179–184 MR0002324 Zbl 0025.30802 Zbl 66.1212.02
[NZ]	I. Niven, H. Zuckerman, "On the definition of normal numbers" Pacific J. Math. , 1 (1951) pp. 103–109 MR0044560 Zbl 0042.26902
[C]	D.G. Champernowne, "The construction of decimals normal in the scale of ten" J. London Math. Soc. , 8 (1933) pp. 254–260 Zbl 0007.33701 Zbl 59.0214.01
[S]	W. Sierpiński, "Démonstration élémentaire d'un théorème de M. Borel sur les nombres absolument normaux et détermination effective d'un tel nombre" Bull. Soc. Math. France , 45 (1917) pp. 127–132 MR0073664 MR0055398 MR0021058 MR1550055
[L]	H. Lebesgue, "Sur certaines démonstrations d'existence" Bull. Soc. Math. France , 45 (1917) pp. 132–144 MR1504765
[Po]	A.G. Postnikov, "Arithmetic modelling of random processes" Trudy Mat. Inst. Steklov. , 57 (1960) (In Russian)

Comments

Almost-all numbers are normal with respect to every base $g$ (see e.g. Theorem 8.11 in [N] or section 9.13 of [HW]). It is not known whether familiar numbers like $\sqrt2,\,e,\,\pi$ are normal or not. Normal numbers are potentially interesting in the context of random number generators. A normal number to a base $g$ is necessarily irrational. The weakly-normal number (to base $10$) $0\cdot12345678901234567890\ldots$ is of course rational. The number $x = 0\cdot1234567891011121314\ldots$, obtained as $x = 0 \cdot \alpha_1 \alpha_2 \alpha_3 \ldots$ where $\alpha_i$ stands for the group of digits representing $i$ to base $10$, is normal to base $10$ [C]. The same recipe works to obtain normal numbers to any given base.

References

[HW]	Hardy, G. H.; Wright, E. M. "An Introduction to the Theory of Numbers", Revised by D. R. Heath-Brown and J. H. Silverman. Foreword by Andrew Wiles. (6th ed.), Oxford: Oxford University Press (2008) [1938] ISBN 978-0-19-921986-5, Zbl 1159.11001
[N]	I. Niven, "Irrational numbers" , Math. Assoc. Amer. (1956) MR1570844 MR0080123 Zbl 0070.27101