Infinite game

A non-cooperative game, in particular a two-person zero-sum game, with infinite sets of player strategies. Let

$$\Gamma = (X_1,X_2,...,X_n,H_1,H_2,...,H_n)$$

be an infinite game with participants. It was shown by C. Berge [1] that if are locally convex compact linear topological Hausdorff spaces, if the pay-off functions are continuous on and are quasi-concave for , , then the game has equilibrium points (solutions). It was also shown [2] that if the are compact Hausdorff spaces and the 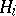are continuous o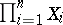n , , then 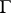has equilibrium points in mixed strategies. However, not all infinite games have equilibrium points, even in mixed strategies. For example, for the two-person zero-sum game in which the sets of player strategies are sets of integers, while the pay-off function has the form

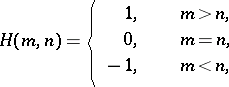no value exists. The best studied classes of infinite games in normal form are infinite two-person zero-sum games and, in particular, games on the unit square (cf. Game on the unit square).

References

[1]	C. Berge, "Théorie génerale des jeux à personnes" , Gauthier-Villars (1957)
[2]	I.L. Gliksberg, "A further generalization of the Kakutani fixed point theorem with application to Nash equilibrium points" Proc. Amer. Math. Soc. , 3 : 1 (1952) pp. 170–174